Нормальное распределение (или распределение Гаусса): что это, от чего зависит и по какому закону работает / Skillbox Media

Содержание:

• Что такое нормальное распределение
• Закон нормального распределения
• Примеры нормального распределения
• Что запомнить

При анализе различных жизненных фактов мы часто встречаемся с нормальным распределением. Например, если кровяное давление вашей бабушки находится в пределах нормы для её возрастной группы, это является положительным знаком. Однако если ваши оценки по математике соответствуют средним показателям общеобразовательной школы, а вы планируете поступить в МФТИ, это может вызвать беспокойство. Важно понимать, что нормальное распределение применяется не только в медицине, но и в образовании, подчеркивая необходимость повышать свои результаты для достижения высоких целей.

В обоих случаях мы анализируем показатели, сравнивая их с установленными нормами и их границами. Эти нормы не формируются произвольно; они рассчитываются на основе данных, полученных из широкого спектра наблюдений. Если визуализировать эти показатели на графике, он будет представлять собой определённую закономерность.

В этой статье мы рассмотрим кривую нормального распределения. Вы узнаете о ее основных характеристиках, значении и применении в различных областях. Также мы обсудим, как кривая нормального распределения используется в статистике и науке для анализа данных. Вы сможете понять, почему нормальное распределение является важным инструментом для исследователей и аналитиков.

• что такое нормальное распределение;
• какие у него есть свойства и формулы;
• где оно применяется.

Что такое нормальное распределение

В статистике распределения играют ключевую роль в анализе частоты различных событий. Распределение можно определить как зависимость между значением переменной и вероятностью, с которой это значение может быть принято. Понимание распределений позволяет глубже анализировать данные и делать обоснованные выводы о вероятностных событиях. Используя распределения, статистики могут оценивать риски, прогнозировать результаты и принимать более информированные решения на основе анализа данных.

При анализе температуры в Караганде на протяжении года можно наблюдать распределение значений, отражающее частоту возникновения температур в различных диапазонах. Например, вероятность того, что температура в определенный день достигнет 25°C, составляет 10%, в то время как вероятность достижения 30°C — 5%. Это демонстрирует, как климатические условия города могут варьироваться и какие температуры наиболее вероятны в течение года. Анализ таких данных позволяет лучше понимать климатические особенности Караганды и предсказывать погодные условия.

Нормальное распределение — это важный статистический концепт, характеризующийся тем, что большинство значений сосредоточено вокруг среднего. Оно также известно как гауссово распределение, закон Гаусса или колоколообразное распределение. Графически нормальное распределение представляется кривой Гаусса, которая демонстрирует симметричную форму, напоминающую колокол. Это распределение широко используется в статистике и вероятностных расчетах, так как многие природные и социальные явления подчиняются этому закономерному поведению.

В статистике нормальное распределение характеризуется тем, что большая часть значений сосредоточена вблизи среднего. Примерно 68,2% всех значений находятся в пределах одного среднеквадратического отклонения от среднего. При увеличении диапазона до двух среднеквадратических отклонений охват увеличивается до 95,4%, а при трех отклонениях — до 99,7%. Это свойство нормального распределения позволяет эффективно анализировать и интерпретировать данные в различных областях, таких как экономика, социология и естественные науки. Понимание этих принципов может помочь в принятии обоснованных решений на основе статистических данных.

Для более наглядного примера рассмотрим группу женщин старше 65 лет и их показатели кровяного давления. Собрав данные о кровяном давлении значительного числа женщин в этой возрастной категории, можно заметить, что большинство значений укладывается в определённый диапазон, в то время как лишь небольшое количество значений значительно отклоняется от этого диапазона. Это наблюдение подчеркивает важность мониторинга кровяного давления у пожилых женщин, поскольку нормальные показатели могут варьироваться, и отклонения могут указывать на необходимость медицинского вмешательства.

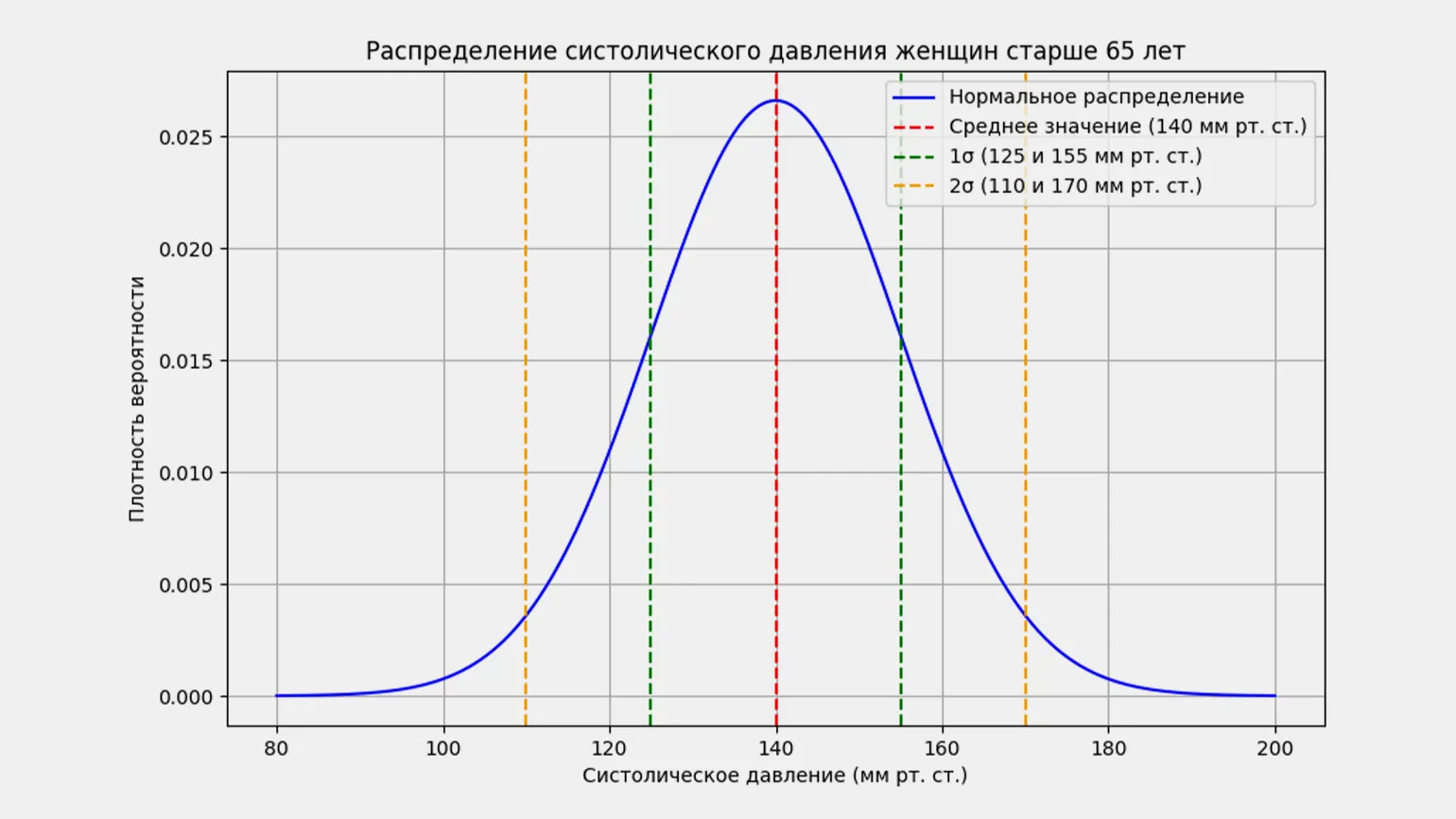
У большинства женщин уровень верхнего давления варьируется от 125 до 155 мм рт. ст., что соответствует отклонению в 15 единиц от среднего значения 140 мм рт. ст. Это отклонение известно как среднее, стандартное или среднеквадратическое отклонение. В статистике оно обозначается греческой буквой σ (сигма), а среднее значение — буквой μ (мю). Понимание этих показателей помогает оценить здоровье сердечно-сосудистой системы и выявить возможные заболевания. Правильный контроль давления является важным аспектом поддержания общего состояния здоровья.

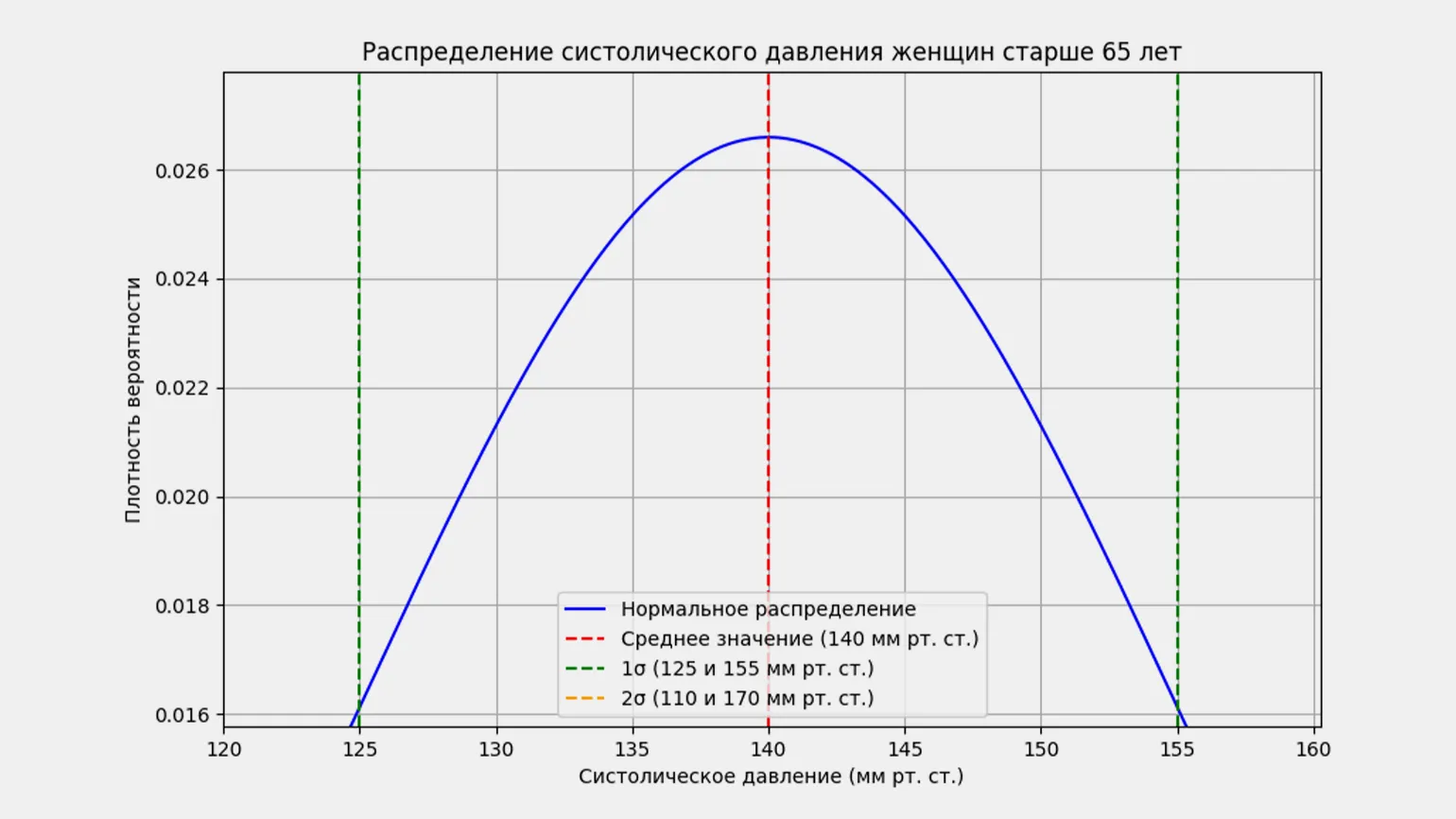
Закон нормального распределения

Сейчас наступит момент, когда страх может овладеть вами.

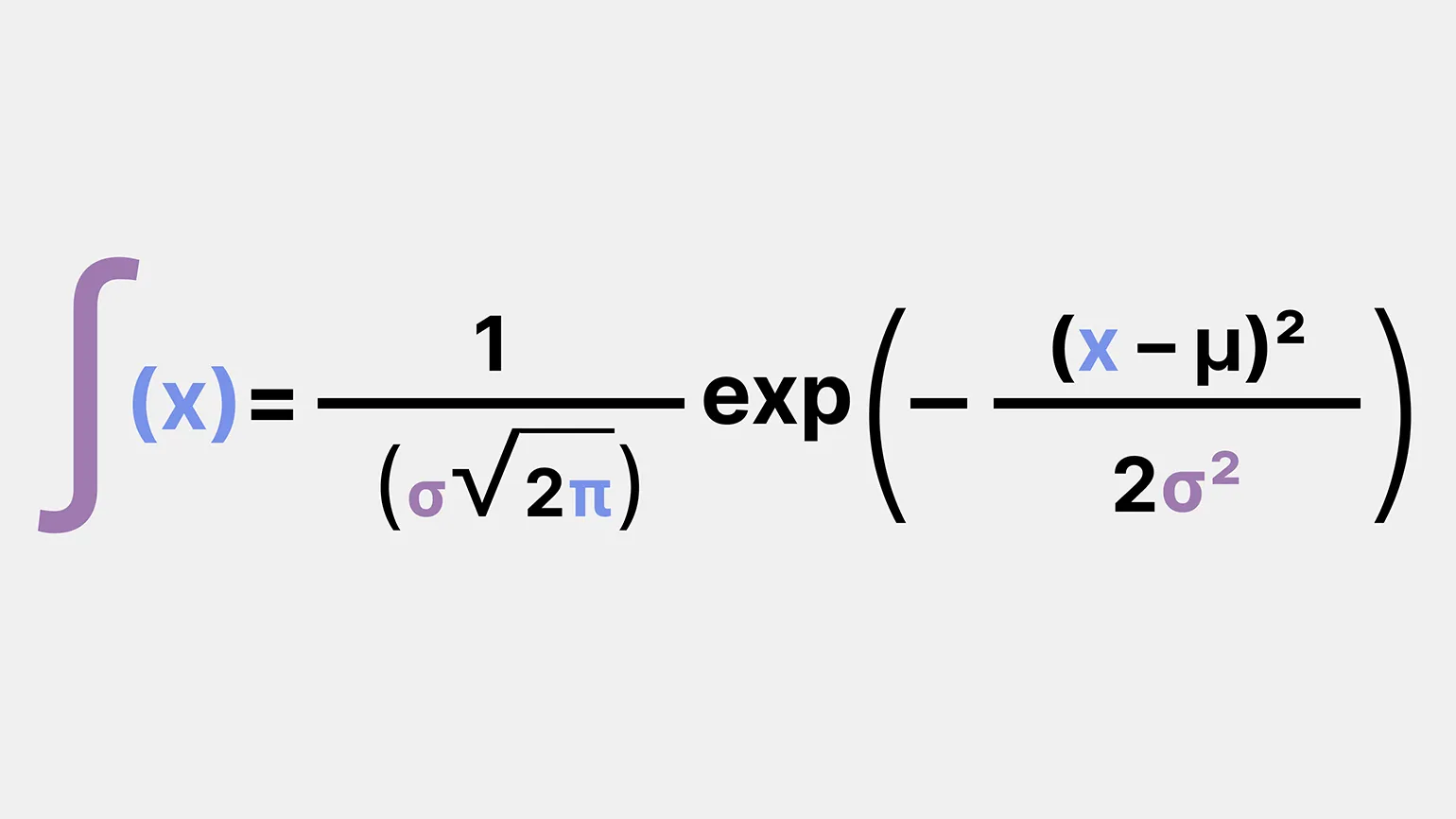
Формула закона нормального распределения может показаться сложной на первый взгляд, но на самом деле она довольно понятна. Начнем с того, что у нас есть важные параметры, которые необходимо учитывать: среднее значение и стандартное отклонение. Эти два параметра позволяют описать форму и характеристики нормального распределения, которое широко используется в статистике и различных областях науки. Понимание этой формулы является ключевым для анализа данных и интерпретации результатов исследований, что делает её важным инструментом для аналитиков и исследователей.

• x — это наше значение;
• μ — среднее значение. Его вычислить просто: делим сумму значений на количество;
• σ — стандартное отклонение. Его вычисляют немного сложнее: нужно найти квадратный корень из среднего значения суммы квадратов разностей между каждым значением и средним.

Возведение стандартного отклонения в квадрат приводит к получению дисперсии. Дисперсия является ключевым показателем, который демонстрирует, насколько сильно наблюдения отклоняются от среднего значения в пределах конкретного распределения. Этот статистический параметр помогает понять степень вариативности данных и играет важную роль в анализе и интерпретации результатов.

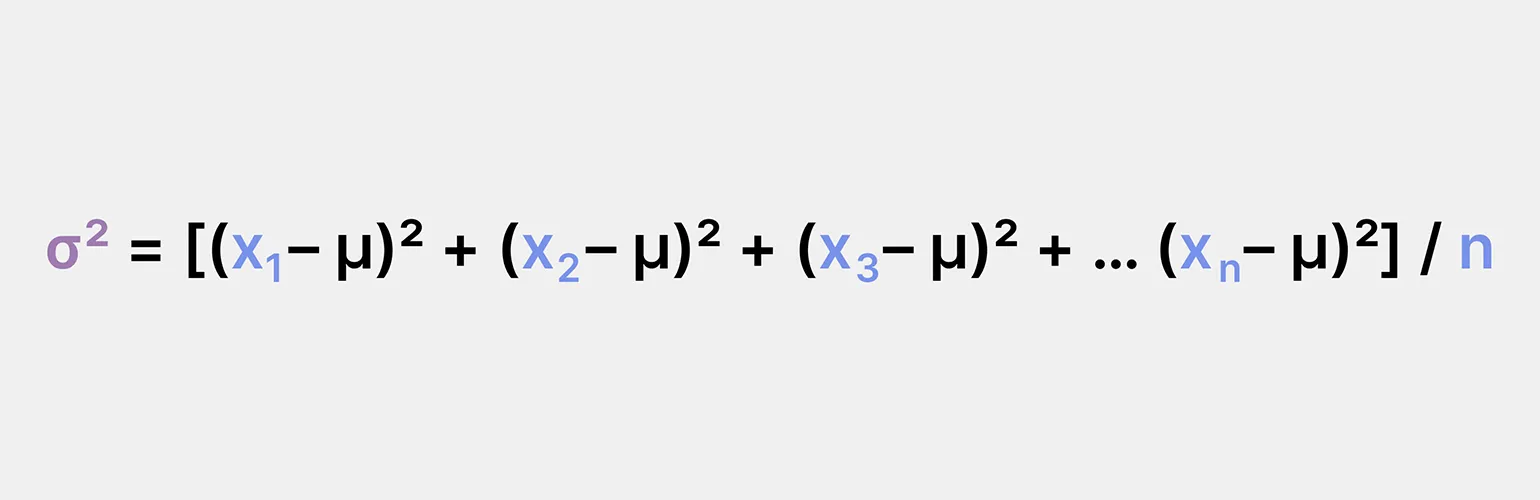
• σ2 — дисперсия;
• x1, x2, x3, … xn — каждое отдельное значение;
• μ — среднее значение;
• n — общее количество значений.

Среднее отклонение вычисляется как квадратный корень из дисперсии. Это важный статистический показатель, который позволяет оценить разброс данных относительно их среднего значения. Среднее отклонение помогает понять, насколько сильно значения в наборе данных отклоняются от среднего значения. Чем меньше среднее отклонение, тем более однородны данные. Напротив, высокое среднее отклонение указывает на значительные колебания. Правильное понимание и использование среднего отклонения играет ключевую роль в статистическом анализе и интерпретации данных.

• π — математическая константа пи (≈ 3,14159), которая представляет собой отношение длины окружности к её диаметру;
• exp — функция возведения основания натурального логарифма e (≈ 2,71828) в степень, значение которой указывается в скобках справа.

Проверим справедливость формулы на примере подбрасывания игральных костей. Поскольку у нас нет возможности подбрасывать настоящие кубики, мы смоделируем процесс, при котором 10 костей будут подбрасываться одновременно 10 000 раз. Для моделирования мы используем язык программирования Python и библиотеки NumPy и SciPy. График распределения результатов подбрасывания будет построен с применением библиотеки Matplotlib. Этот подход позволит нам визуализировать распределение результатов и проанализировать, насколько оно соответствует теоретическим ожиданиям.

Если вы обладаете навыками работы с Python и знакомы с его библиотеками, вы можете воспроизвести наши шаги. Обратите внимание, что в приведенном коде применяются методы библиотеки NumPy, что может привести к небольшим различиям в ваших результатах. Тем не менее, график распределения сохранит характерную форму — гауссовскую. Использование NumPy позволяет эффективно обрабатывать массивы данных и строить визуализации, что делает его незаменимым инструментом для анализа статистических данных.

Результат выполнения кода представляет собой вывод, который зависит от логики и структуры самого кода. Необходимо учитывать, что в зависимости от языка программирования и используемых библиотек, результат может варьироваться. Обычно результатом выполнения является текст, числовые значения, графические элементы или изменения в состоянии программы. Для точного понимания результата важно проанализировать код, выявить его основные функции и логику работы. Это позволит определить, как именно код влияет на данные и какой вывод он генерирует при различных условиях.

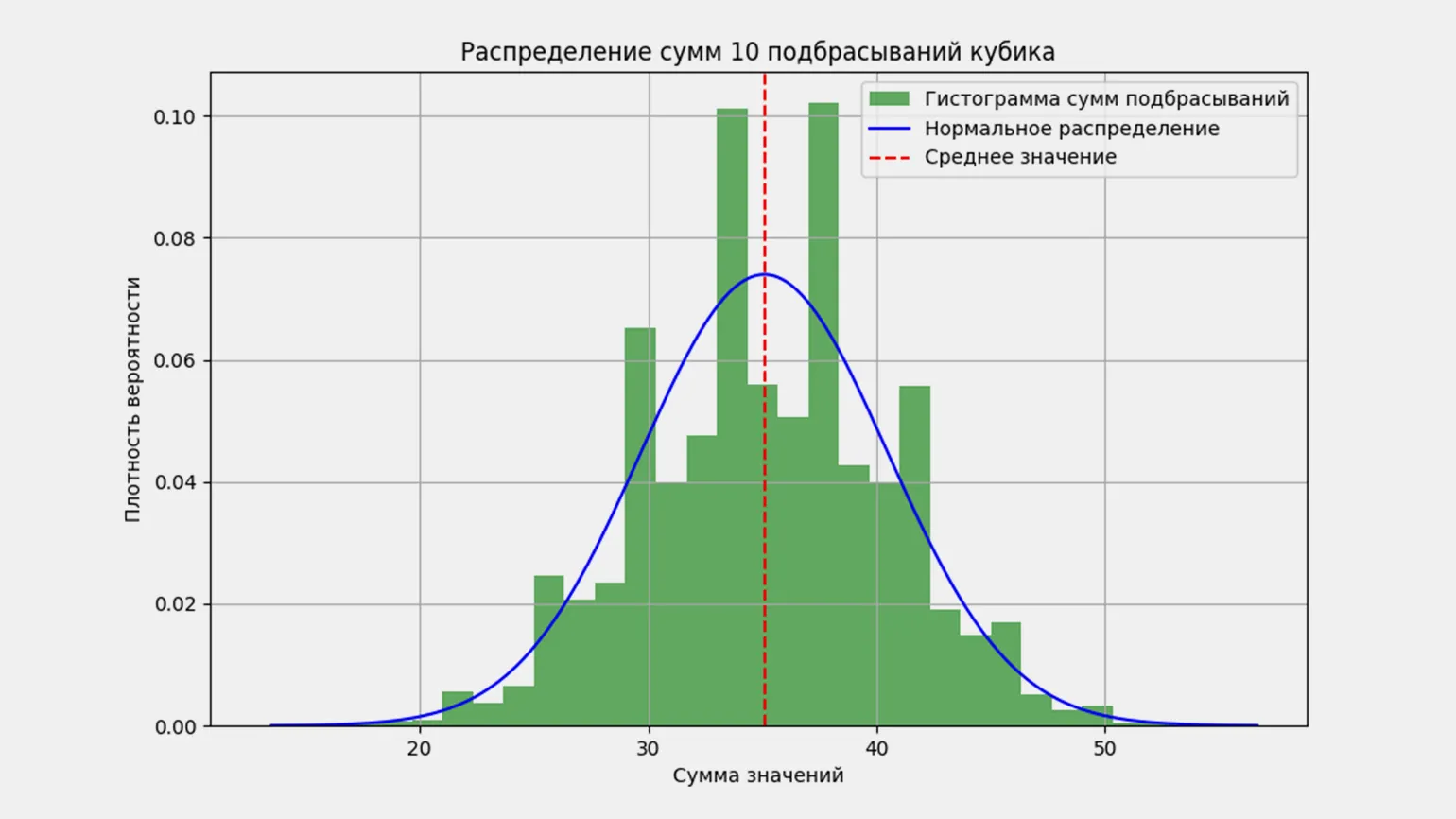
Проверьте формулу с помощью нашего кода, если у вас нет возможности записать её на бумаге.

Мы определили среднее значение μ = 35 и стандартное отклонение σ = 5,402. Для проверки этих данных используем калькулятор OwlCalculator. Вводим значения в калькулятор, выбирая значение x в диапазоне от 10 до 60. В качестве примера возьмем значение 32. Калькулятор предоставит значение функции плотности вероятности для указанного x, что позволит нам оценить вероятность наблюдения данного значения в рамках нормального распределения.

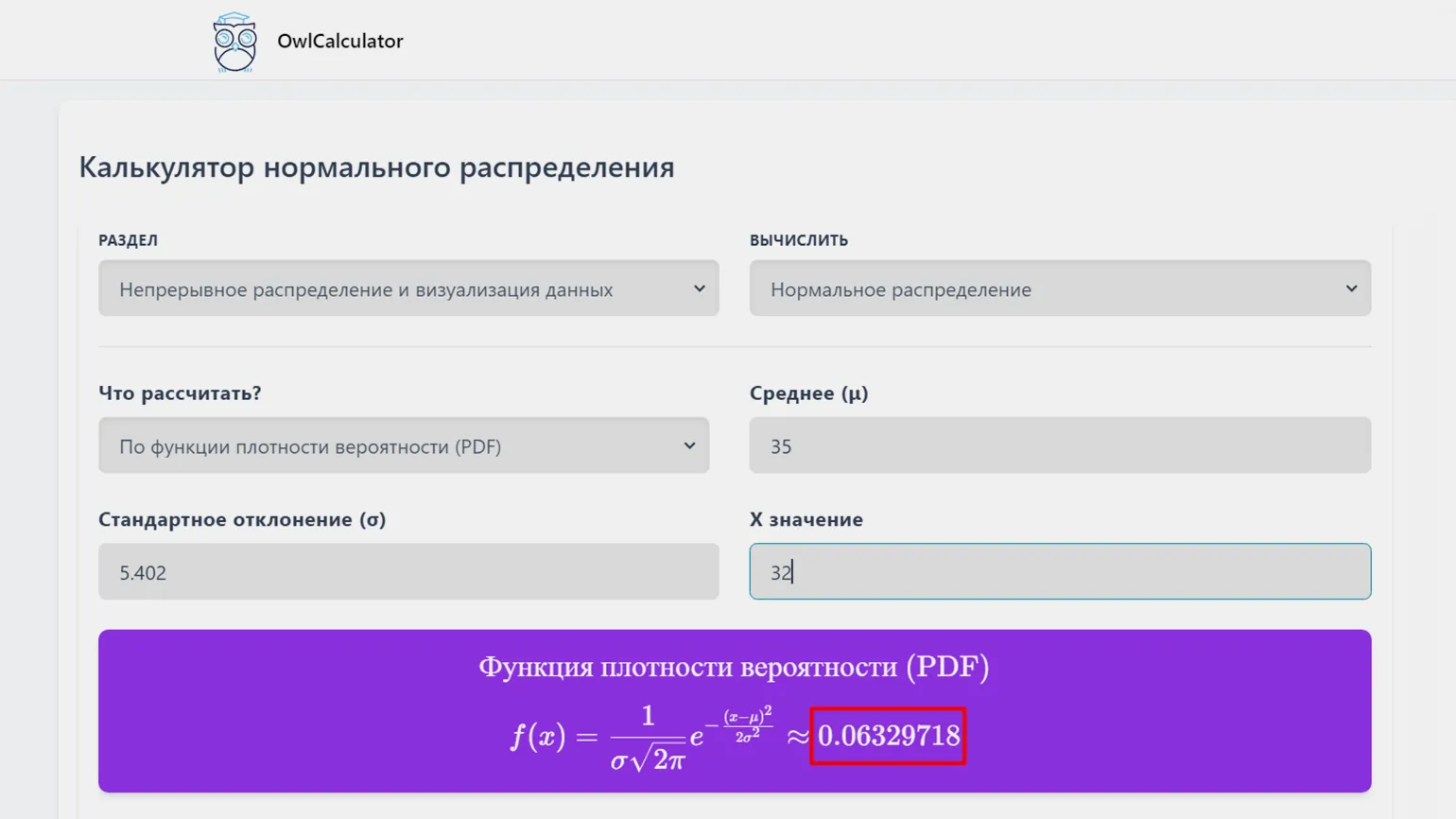
Точно утверждать сложно, однако примерно это соответствует графику. Давайте создадим гистограмму с уменьшенным масштабом для проверки. Это позволит более детально проанализировать данные и выявить возможные отклонения.

Здесь становится очевидным, что значение гистограммы практически совпадает с результатами, полученными с помощью калькулятора. Это подтверждает точность и надежность представленных данных.

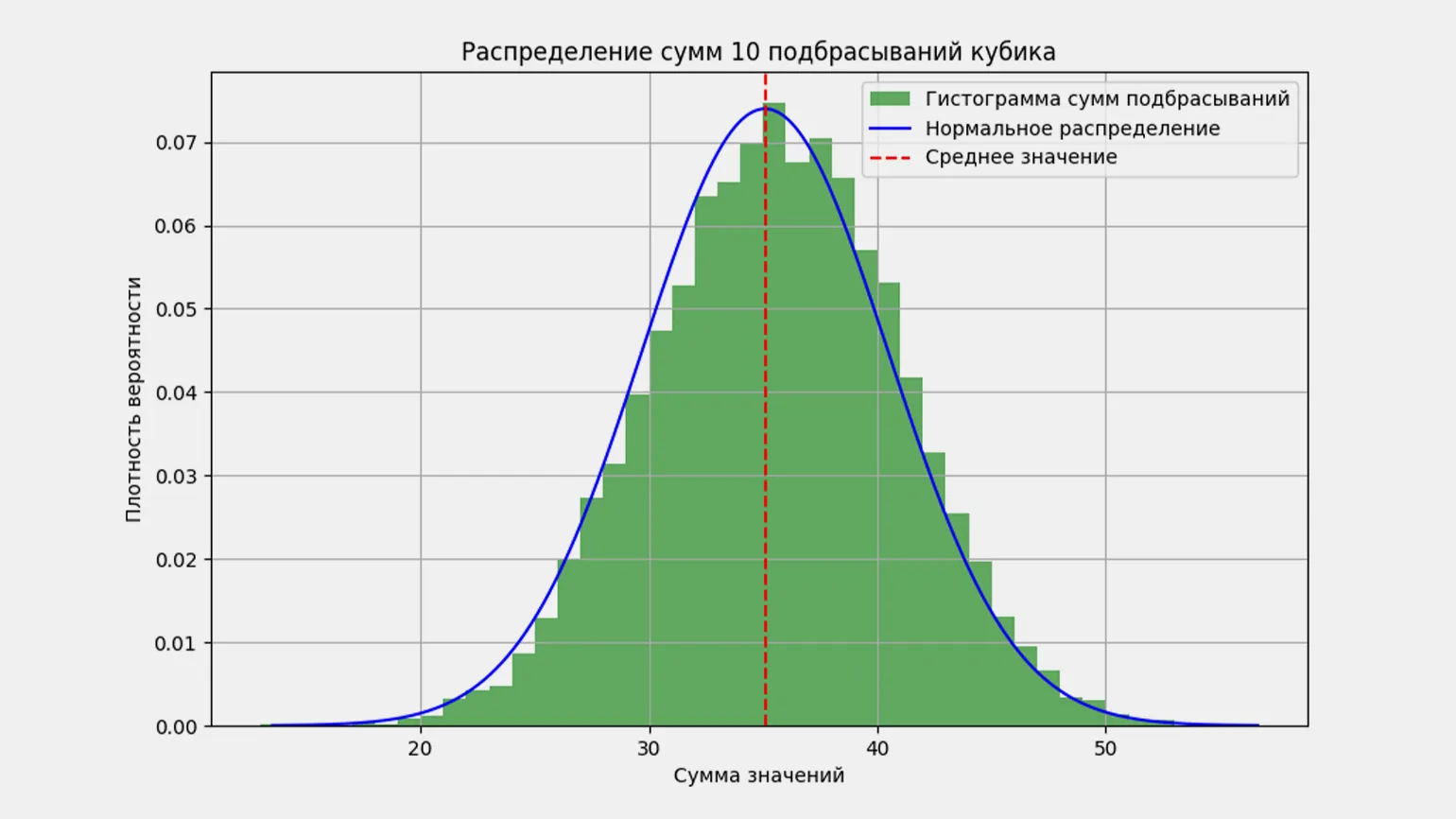
Читайте также:

Изучение программирования на Python

Python является одним из самых популярных языков программирования в мире. Он подходит как для начинающих, так и для опытных разработчиков благодаря своей простоте и мощным возможностям. Начать программировать на Python можно с освоения базовых концепций, таких как синтаксис, переменные, операторы и структуры данных.

Python поддерживает множество парадигм программирования, включая объектно-ориентированное, функциональное и императивное программирование. Это делает его универсальным инструментом для решения различных задач, от разработки веб-приложений до анализа данных и машинного обучения.

Современные библиотеки и фреймворки, такие как Django и Flask, позволяют создавать мощные веб-приложения, а библиотеки, такие как NumPy и Pandas, упрощают работу с данными.

Чтобы начать программировать на Python, вам потребуется установить интерпретатор Python и выбрать подходящий текстовый редактор или интегрированную среду разработки (IDE). Рекомендуется изучать язык через практику, создавая небольшие проекты и решая задачи.

Существует множество ресурсов для изучения Python, включая онлайн-курсы, книги и форумы. Сообщество Python активно и готово помочь новичкам, поэтому не стесняйтесь обращаться за помощью и делиться своими вопросами.

Изучение программирования на Python открывает множество возможностей для карьерного роста и профессионального развития. Начните свой путь в программировании уже сегодня и откройте для себя мир технологий и инноваций.

Примеры нормального распределения

Закон распределения Гаусса отличается своей универсальностью и находит применение в самых разных областях, включая маркетинг. Например, если вы управляете интернет-магазином, анализ распределения сумм покупок клиентов позволяет лучше понять их поведение. Эти данные могут служить основой для оптимизации маркетинговой стратегии и более эффективного распределения целевой рекламы. Понимание того, как клиенты тратят деньги, помогает выделить сегменты аудитории, что способствует улучшению взаимодействия с клиентами и увеличению продаж.

Вы анализируете данные о суммах покупок всех клиентов за последний месяц. Предположим, у вас есть информация о 1000 транзакциях. Теперь необходимо рассчитать среднее значение и стандартное отклонение этих сумм. В качестве гипотезы предполагается, что суммы покупок распределены нормально, основываясь на полученных значениях μ (математическое ожидание) и σ (стандартное отклонение). Такой анализ поможет выявить общие тенденции в покупательском поведении и может быть полезен для планирования маркетинговых стратегий.

В ходе проведенных расчетов было установлено, что средний чек составляет 5000 рублей, в то время как стандартное отклонение составляет 1000 рублей. Эти данные могут быть полезны для анализа покупательского поведения и оценки финансовых показателей. Средний чек отражает типичный расход клиентов, а стандартное отклонение позволяет понять, насколько варьируются суммы покупок от этого среднего значения. Такой анализ помогает в принятии обоснованных управленческих решений и стратегическом планировании.

В данном анализе мы устанавливаем контрольные границы на уровне ±2σ от среднего значения, что позволяет охватить примерно 95% всех наблюдаемых значений в рамках нормального распределения. В нашем случае контрольные границы составляют от 3000 до 7000 рублей. Этот подход обеспечивает надежную оценку диапазона значений и помогает в выявлении отклонений от нормы, что важно для дальнейшего анализа данных и принятия обоснованных решений в финансовой сфере.

На основе проведённых расчётов предоставляем отделу маркетинга следующие рекомендации:

• Если клиент тратит больше 7000 рублей, его можно считать высокоценным и стоит направить на него больше маркетинговых усилий.
• Если клиент тратит меньше 3000 рублей, то это указывает на возможность улучшения маркетинговых стратегий для увеличения среднего чека.

Отдел маркетинга теперь оптимизирует рекламные кампании, направляя основную часть бюджета на привлечение высокоценных клиентов. Это позволит эффективно расходовать рекламные средства и минимизировать их нецелевую трату, что в свою очередь повысит общую рентабельность инвестиций в рекламу. Сосредоточение на качественных лидах обеспечит значительное улучшение результатов и укрепит позиции компании на рынке.

Маркетинг — не единственная сфера, где используется распределение Гаусса. Этот статистический инструмент находит применение в различных областях, включая финансы и биологию. Распределение Гаусса помогает анализировать данные и принимать обоснованные решения, основываясь на статистических методах. Благодаря своей универсальности, оно позволяет выявлять закономерности и тенденции в больших объемах информации, что особенно важно для успешного управления и прогнозирования в разных отраслях.

• в физике — для описания случайных ошибок измерений;
• в биологии — для описания распределения размеров, веса и других характеристик популяций;
• в психологии — для описания распределения IQ и других психологических показателей;
• в экономике — для моделирования распределения доходов, цен и других экономических показателей;
• в демографии — для анализа роста численности населения;
• в инженерном деле — для контроля качества продукции;
• в статистическом контроле процессов — для мониторинга производственных параметров;
• в исследованиях — для обработки результатов экспериментов и опросов;
• в методах оценки и аппроксимации — для предсказания значений на основе известных данных и упрощения сложных функций или распределений.

Что запомнить

• Нормальное распределение (распределение Гаусса, колоколообразное распределение) — это тип распределения, при котором большинство значений сосредоточено около среднего значения.
• Среднее значение μ (мю) и стандартное отклонение σ (сигма) определяют форму кривой нормального распределения (гауссианы).
• По закону нормального распределения 68,2% значений находятся в пределах одного σ от μ, 95,4% — в пределах двух σ, а 99,7% — в пределах трёх σ.
• Зная среднее значение и стандартное отклонение распределения, можно устанавливать контрольные границы и принимать решения на их основе.
• Нормальное распределение широко применяется в различных областях: естественных науках (физика, биология), социальных науках (экономика, демография), психологии, производственных процессах, исследованиях и анализе данных.

Узнайте больше о кодировании и программировании в нашем телеграм-канале. Подписывайтесь, чтобы не пропустить актуальные новости и полезные материалы!

Ознакомьтесь с дополнительными материалами:

• Как установить библиотеку в Python: руководство для новичка
• Модуль random в Python
• Работаем с Pandas: основные понятия и реальные данные