Числа с плавающей точкой: 5 важных фактов для новичков

Содержание:

• История появления чисел с плавающей точкой: кто стоит за этим стандартом?
• Понимание фиксированной точки в вычислениях
• Понимание чисел с плавающей точкой
• Как осуществляется представление чисел с плавающей точкой
• Понимание особенностей чисел с плавающей точкой
• Ключевые моменты для усвоения

История появления чисел с плавающей точкой: кто стоит за этим стандартом?

В 1970-х годах, в период активного развития компьютерной революции, учёные и программисты tirelessly трудились над созданием новых компьютеров и алгоритмов. Их основная задача заключалась в демонстрации потенциала этих инноваций, способных радикально преобразовать мир вычислений. Эти усилия стали основой для дальнейшего прогресса в области информационных технологий, что в итоге привело к созданию мощных вычислительных систем и сложных программных решений, изменивших подход к обработке данных и взаимодействию с информацией.

В то время каждый компьютер работал по своему, используя уникальные операционные системы и различные методы представления данных. Такая ситуация приводила к значительным трудностям, поскольку перенос программного обеспечения с одного устройства на другое требовал больших усилий, включая полную переработку программ под новую архитектуру. Это создавало проблемы для разработчиков и пользователей, так как совместимость программного обеспечения была ограничена, что затрудняло обмен данными и интеграцию различных систем.

Унификация представления чисел стала одной из самых сложных задач в разработке программного обеспечения. Разнообразие форматов чисел требовало от программистов значительных затрат времени и усилий, что часто приводило к изменению логики работы приложений. Это, в свою очередь, негативно сказывалось на стабильности и производительности программ. Эффективное решение этой проблемы позволяет улучшить качество кода и повысить эффективность разработки.

Признание важности стандартизации представления вещественных чисел стало основой для формирования проектной группы в компании Intel, состоящей из ведущих инженеров. Эта инициатива возникла в условиях растущей конкуренции, когда другие компании, такие как DEC, также начали активно разрабатывать собственные решения в этой области. Стандартизация представления вещественных чисел играет ключевую роль в обеспечении совместимости и эффективности вычислительных процессов, что делает её актуальной для всех участников рынка.

Началась активная гонка за создание оптимального стандарта. Каждая компания стремилась продвигать свои разработки, надеясь, что именно их решение станет общепринятым. В это время крупные игроки, такие как IBM и Cray, внимательно следили за ситуацией, ожидая, когда появится очевидный лидер, чтобы интегрировать его стандарт в свои системы. Ситуация подчеркивает важность стандартизации в индустрии, так как единственный стандарт может существенно упростить взаимодействие и совместимость технологий.

В результате всех проведенных разработок остались два ключевых стандарта: спецификация K-C-S от компании Intel и архитектура VAX от DEC. У каждого из этих стандартов есть свои достоинства и недостатки, которые влияют на их использование в различных вычислительных системах. Спецификация K-C-S предлагает определенные преимущества в производительности, в то время как VAX отличается своей универсальностью и совместимостью с различными программными решениями. Эти аспекты делают оба стандарта значительными в истории компьютерной архитектуры.

• Десятичный формат, удобный для восприятия человеком, но менее эффективный для вычислений.
• Высокая точность благодаря десятичному представлению, что уменьшает ошибки округления, особенно при работе с большими числами.
• Включение специальных значений, что облегчало работу с ошибками и предотвращало переполнения.

• Двоичный формат, обеспечивающий высокую эффективность вычислений на соответствующих системах.
• Широкое распространение, что позволяло легко адаптировать спецификацию VAX под различные устройства.
• Оптимизированная производительность, требующая меньше вычислительных ресурсов.

Компания DEC стремилась сделать VAX общепринятым стандартом, активно убеждая ведущих ученых в том, что архитектура K-C-S не сможет достичь сопоставимой производительности. Однако Intel обладала своими преимуществами, включая уникальные секреты оптимизации и передовые технологии, которые позволили ей опередить конкурентов. Конкуренция между DEC и Intel в области вычислительных архитектур подчеркивает важность инновационных решений и стратегического подхода в высоких технологиях.

Intel одержала победу, и её спецификация легла в основу стандарта IEEE 754, который был официально утверждён Институтом инженеров электротехники и электроники (IEEE) в 1985 году. Этот стандарт продолжает использоваться в современных вычислениях и программировании, гарантируя высокую степень совместимости и точности. Стандарт IEEE 754 стал ключевым элементом в разработке числовых вычислений, обеспечивая надежное представление чисел с плавающей запятой и стандартизированные операции, что значительно упростило работу разработчиков и повысило качество программного обеспечения.

Понимание фиксированной точки в вычислениях

Фиксированная точка — это метод представления чисел в двоичной системе, широко используемый в вычислительной технике. Для понимания работы стандарта IEEE 754 необходимо сначала изучить основы представления чисел. Компьютеры обрабатывают десятичные числа в двух основных форматах: с фиксированной точкой и с плавающей точкой. Формат с фиксированной точкой позволяет точно представлять числа, что делает его особенно полезным в приложениях, требующих высокой точности, таких как финансовые расчеты. Стандарт IEEE 754, в свою очередь, определяет правила для работы с числами с плавающей точкой, что обеспечивает большую гибкость при обработке значений с различной степенью точности. Оба формата имеют свои преимущества и недостатки, и выбор между ними зависит от конкретных задач и требований.

Хотя в данной статье мы используем термин «точка», стоит подчеркнуть, что в англоязычной литературе часто употребляется слово «запятая». Оба термина обозначают одно и то же, но в русскоязычных источниках более распространён первый вариант.

Числа с фиксированной точкой — это двоичные числа, в которых длина целой и дробной частей строго ограничена. В 16-битном представлении, например, можно выделить 10 бит для целой части и 6 бит для дробной. Это позволяет эффективно хранить и обрабатывать числовые данные в системах, где важна точность и контроль за занимаемой памятью. Числа с фиксированной точкой широко используются в цифровой обработке сигналов и встраиваемых системах, где ресурсы ограничены, а производительность критична.

Разделение чисел на целую и дробную части осуществляется с помощью точки. При интерпретации числа компьютером используется 16-битная система, где 10 бит отводится для представления целой части, а 6 бит — для дробной. Пример ниже наглядно демонстрирует этот принцип.

На изображении отображено двоичное число, которое соответствует десятичному значению 689.6875. Для лучшего понимания системы счисления рассмотрим еще один пример, где закодировано число 13.0. Данная иллюстрация помогает визуализировать преобразование десятичных чисел в двоичную систему, что может быть полезно для изучения основ компьютерной арифметики.

В данном случае наблюдаем, что дробная часть числа состоит исключительно из нулей, что свидетельствует об отсутствии значимой дробной части в десятичном представлении. Это означает, что число является целым.

Для понимания работы фиксированной точки важно проанализировать целую часть числа. Она представляется в двоичной системе, где каждый бит соответствует степени двойки. Например, число 13 можно разложить на степени двойки следующим образом: 13 в двоичной системе записывается как 1101. Это означает, что 13 равно 1 умножить на 2 в кубе (8) плюс 1 умножить на 2 во второй степени (4) плюс 0 умножить на 2 в первой степени (2) плюс 1 умножить на 2 в нулевой степени (1). Таким образом, 13 = 8 + 4 + 0 + 1. Понимание этого процесса имеет ключевое значение для работы с фиксированной точкой, так как позволяет эффективно представлять и обрабатывать целые числа в цифровых системах.

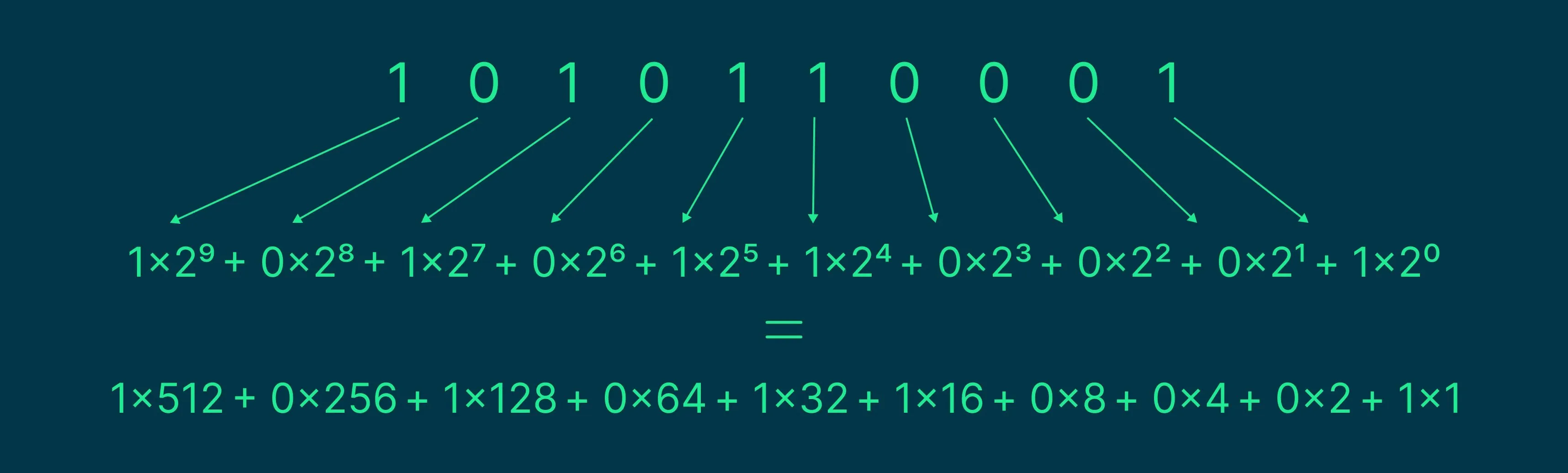
Для преобразования двоичного числа в десятичное нужно суммировать все степени двойки, соответствующие единичным битам. Каждая позиция в двоичном числе представляет степень двойки, начиная с нуля справа. Например, если в двоичном числе есть единицы на позициях 0, 2 и 4, то необходимо сложить 2 в степени 0, 2 в степени 2 и 2 в степени 4. Полученный результат будет десятичным эквивалентом исходного двоичного числа.

Теперь рассмотрим дробную часть числа. Принцип преобразования дробной части аналогичен преобразованию целой, но здесь используются отрицательные степени двойки. Для примера возьмем число 689.6875.

Сначала выделим целую и дробную части. Целая часть 689 будет преобразована в двоичный код, а дробная часть 0.6875 — с помощью отрицательных степеней двойки.

Для дробной части мы умножаем ее на 2 и фиксируем целую часть результата. Повторяем процесс с оставшейся дробной частью, пока не достигнем требуемой точности или пока дробная часть не станет равной нулю.

Таким образом, преобразование дробной части позволяет нам получить двоичный код, который точно представляет исходное число в двоичной системе счисления.

Степени в данной системе начинаются с -1 и продолжают уменьшаться: -2, -3 и так далее. Для преобразования отрицательных степеней в положительные достаточно взять дробь. Чтобы получить итоговое значение, необходимо сложить все степени, где бит равен 1.

Теперь объединим целую и дробную части числа. Этот процесс позволяет получить одно целое значение, которое включает в себя как целую, так и дробную часть, что упрощает дальнейшие математические операции. Объединение целой и дробной частей особенно важно в различных областях, таких как бухгалтерия, инженерия и программирование, где точные вычисления играют значительную роль. Правильное понимание данной темы поможет вам избежать ошибок при работе с числами и повысит вашу математическую грамотность.

Преимущества фиксированной точки заключаются в том, что такие представления всегда имеют конечную длину. Например, число Пи может быть округлено до определённого знака после запятой, а лишние цифры будут отброшены. Это позволяет эффективно управлять памятью и повышает скорость вычислений, особенно в системах, где важна точность и стабильность результатов. Фиксированная точка также упрощает работу с числовыми данными, так как исключает проблемы, связанные с бесконечными десятичными дробями, характерными для представления чисел с плавающей запятой.

Число Пи представляется как приближённое значение, которое не отражает его точное значение. Пи, обозначаемое символом π, является математической константой, используемой для вычисления соотношения длины окружности к её диаметру. Значение числа Пи примерно равно 3.14, но это лишь его округлённая форма. В действительности Пи — это бесконечная непериодическая десятичная дробь, что делает его уникальным в математике и науке. Понимание Пи имеет важное значение для различных областей, включая геометрию, физику и инженерное дело.

Фиксированная точка обладает определёнными недостатками. Рассмотрим 16-битные числа, где 10 бит отведены для целой части, а 6 бит — для дробной. В данной конфигурации диапазон значений будет ограничен. Это может создать сложности при работе с числами, требующими более широкого диапазона, что влияет на точность вычислений и может привести к переполнению. Понимание этих ограничений важно для оптимизации программ и алгоритмов, особенно в контексте числовых вычислений и графики.

Фиксированная точка имеет значительный недостаток, который стоит учитывать. Рассмотрим максимальное число, которое может быть представлено в данной системе, и число, на единицу меньшее. Разница между этими значениями составит не 0.000001, как в десятичной системе, а 0.015625. Эта величина определяет минимальный шаг в системе фиксированной точки и указывает на предел точности, с которой можно производить вычисления. Понимание этих характеристик является ключевым для эффективного использования фиксированной точки в программировании и численных методах.

При добавлении следующего числа разница останется неизменной. Это означает, что при увеличении последовательности чисел разница между ними не изменится, что может быть полезно для анализа числовых рядов и математических последовательностей. Понимание этого принципа важно для различных областей, включая статистику и экономику, где постоянство разницы может влиять на прогнозирование и моделирование данных.

Высокая точность преобразования десятичных чисел в двоичные форматы значительно оптимизирует вычислительные процессы и уменьшает нагрузку на компьютер. Благодаря этому, система четко различает, какие биты представляют собой целую часть, а какие — дробную. Это позволяет повышать эффективность обработки данных и улучшает производительность программного обеспечения.

Теперь, когда мы обсудили фиксированные числа, можно перейти к числам с плавающей точкой и подробно рассмотреть стандарт IEEE 754. Этот стандарт описывает представление чисел с плавающей точкой в компьютерных системах, обеспечивая единообразие и совместимость между различными вычислительными платформами. Понимание IEEE 754 важно для разработчиков программного обеспечения и инженеров, так как он влияет на точность и производительность вычислений. Рассмотрим основные аспекты стандарта, включая формат представления, операции над числами и вопросы, связанные с округлением.

Понимание чисел с плавающей точкой

В программировании число с плавающей точкой, также известное как число с плавающей запятой, представляет собой числовое значение, используемое для обозначения вещественных чисел. Это представление обеспечивает возможность работы с числами различной величины и точности, что является важным аспектом при выполнении вычислений в различных областях, таких как научные расчеты, графика и финансовые приложения. Использование чисел с плавающей точкой позволяет эффективно управлять диапазоном значений и минимизировать ошибки округления, что делает их незаменимыми в современном программировании.

Двоичное представление чисел с плавающей точкой включает три основных компонента: знаковый бит, экспоненту и мантиссу. Знаковый бит определяет, является ли число положительным или отрицательным. Экспонента отвечает за масштабирование числа, позволяя представлять как очень большие, так и очень маленькие значения. Мантисса, в свою очередь, содержит значимые цифры числа. Эти три элемента совместно обеспечивают точное представление чисел с плавающей точкой в вычислительных системах, что критически важно для выполнения сложных математических операций и обработки данных.

• Знаковый бит определяет, является ли число положительным или отрицательным.
• Экспонента указывает, на сколько раз нужно умножить мантиссу.
• Мантисса представляет собой фиксированное количество битов, отражающее точность числа.

Научная нотация является важным инструментом для представления чисел, особенно когда речь идет о больших или очень малых значениях. Она позволяет записывать числа в компактной форме, используя множитель и степень десяти. Например, число 123.456 можно выразить как 1.23456 × 10^2. Такой формат не только упрощает чтение и запись чисел, но и облегчает выполнение математических операций, таких как сложение, вычитание, умножение и деление. Научная нотация широко используется в научных расчетах, инженерии и других областях, где необходимо работать с разнообразными диапазонами чисел.

Рассмотрим умножение 0.0006 на 0.0002. В научной нотации это выражение можно упростить, складывая степени и выполняя простое умножение. В отличие от обычной формы, где легко запутаться из-за большого количества нулей, научная нотация позволяет четко и быстро производить вычисления. Это делает работу с малыми числами более понятной и удобной.

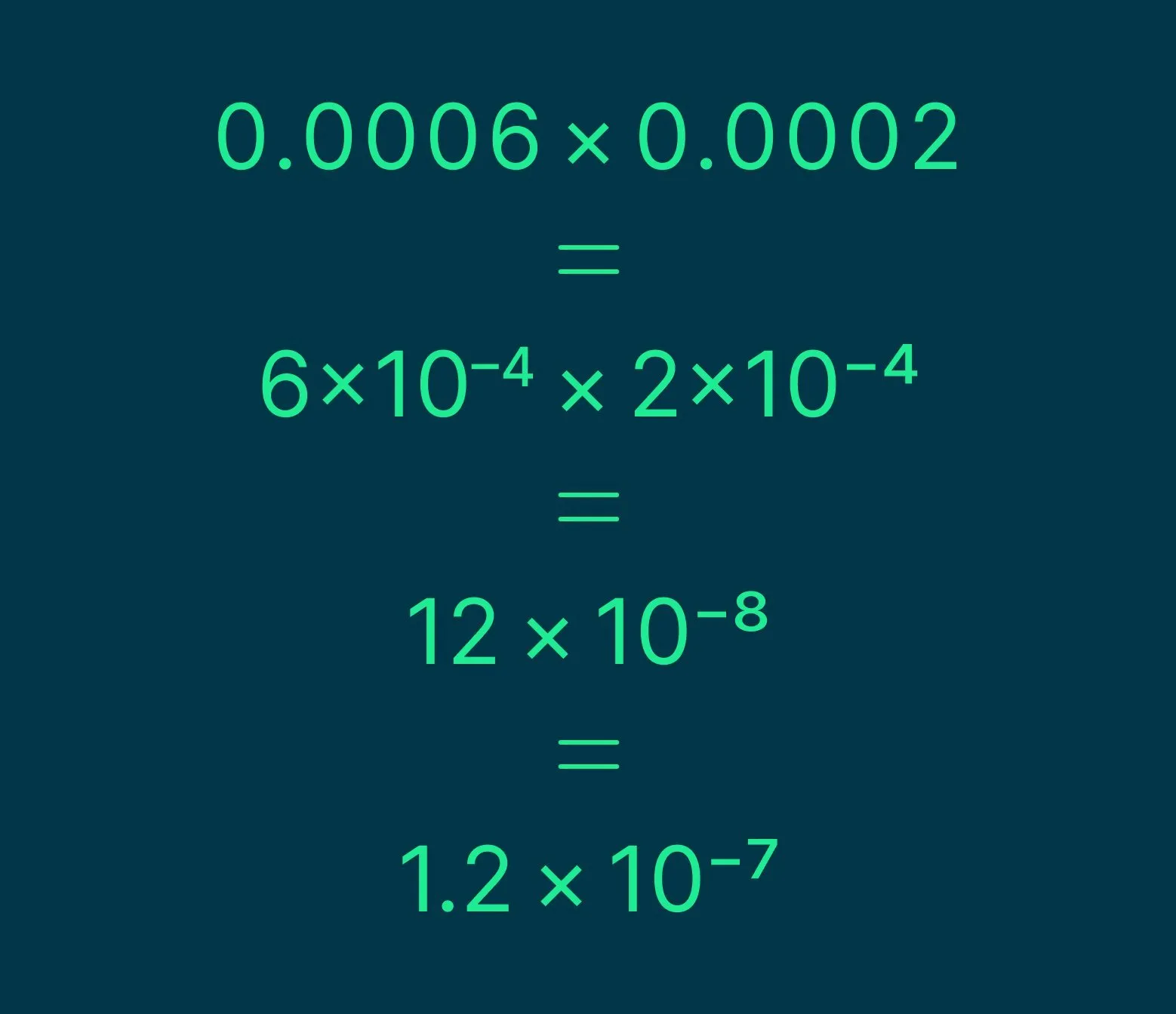
Научная нотация представляет собой удобный способ представления чисел, что значительно упрощает выполнение математических операций. Этот формат позволяет эффективно работать как с очень большими, так и с очень маленькими числами, делая их более доступными для анализа и вычислений. Использование научной нотации делает математику более понятной и способствует быстрому решению сложных задач.

В научной нотации число представлено тремя основными компонентами: знаком, коэффициентом (или мантиссой) и экспонентой. Эта форма записи позволяет удобно выражать как очень большие, так и очень маленькие числа, упрощая их использование в математических и научных расчетах. Знак указывает на положительное или отрицательное значение, коэффициент определяет числовую часть, а экспонента указывает на степень, к которой следует возвести число 10. Использование научной нотации значительно облегчает работу с большими данными и улучшает точность вычислений.

• Знак числа (положительный или отрицательный) позволяет работать с положительными величинами, которые затем можно преобразовать в отрицательные при необходимости.
• Коэффициент — это основная часть числа, находящаяся обычно в диапазоне от 1 до 9, но для чисел с плавающей точкой он варьируется от 0 до 1.
• Мантисса представляет собой дробную часть коэффициента.
• Экспонента указывает, на сколько мы умножаем коэффициент.

Число 1.2 × 10^−7 можно выразить в стандартной форме. Это значение представляет собой научное обозначение, где 1.2 является коэффициентом, а 10^−7 указывает на степень, что означает деление на 10 в седьмой степени. Таким образом, 1.2 × 10^−7 равно 0.00000012. Данная форма записи удобна для работы с очень большими и очень маленькими числами, что делает её популярной в научных и инженерных расчетах.

Компоненты числа включают положительный знак +1, мантиссу 0.12 и экспоненту −8.

Число 10 является основанием десятичной системы счисления, но его можно заменить на другое значение. Например, рассмотрим преобразование числа 0.12 × 10^−8 в систему счисления с основанием 5. Это позволяет исследовать, как различные основания влияют на представление чисел и их значения в математике и программировании. Понимание преобразования чисел между системами счисления является важным аспектом в различных областях, таких как информатика и инженерия.

Несмотря на изменение мантиссы, экспонента осталась неизменной, поскольку мы следовали основным правилам умножения.

Экспонента остается неизменной, потому что мы разбиваем число 10 на множители 5 и 2. Если исходная степень равна −8, то мы можем представить число 10 как произведение 5^−8 и 2^−8. Это объясняет, почему экспонента не претерпевает изменений при таком разложении.

Теперь обратим внимание на двоичное представление чисел, где основанием является число 2, подобно тому, как в десятичной системе основанием служит число 10. В этой системе мантисса будет находиться в диапазоне от 0 до 1, исключая 1. Двоичное представление используется в вычислительных системах и цифровой электронике, так как позволяет эффективно обрабатывать информацию. Понимание принципов двоичной системы является ключевым для изучения компьютерных наук и программирования.

Десятичное число 0.12 × 10^−8 в двоичной системе счисления преобразуется в следующее значение. Для перевода десятичного числа в двоичное необходимо учитывать как целую, так и дробную часть. Данное число, представлено в научной нотации, сначала преобразуется в десятичный формат. После этого выполняется конвертация в двоичную систему. Результирующее двоичное представление позволяет более эффективно обрабатывать данные в компьютерных системах.

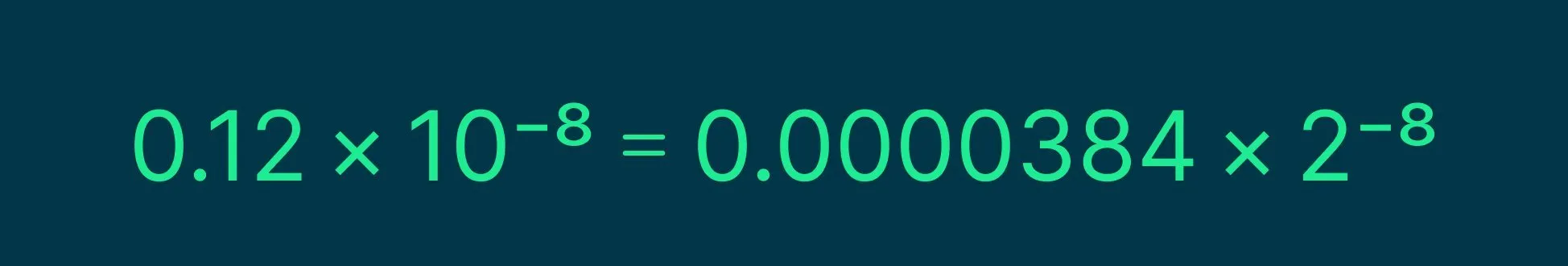
Научная нотация представляет собой ключевой принцип, который лежит в основе двоичного представления десятичных чисел в компьютерных системах. В этом контексте особое внимание стоит уделить стандарту IEEE 754, который определяет формат представления вещественных чисел и их арифметические операции. Стандарт IEEE 754 широко применяется в современных вычислениях, обеспечивая высокую точность и эффективность обработки чисел с плавающей точкой. Рассмотрим его основные аспекты и влияние на расчетные процессы в компьютерной технике.

Как осуществляется представление чисел с плавающей точкой

Стандарт IEEE 754 является ключевым набором правил, который определяет кодирование вещественных чисел в компьютерных системах. Он стал де-факто стандартом в программировании, особенно в области арифметики чисел с плавающей точкой. Этот стандарт обеспечивает универсальный способ представления и работы с вещественными числами, что критически важно для высокоточных вычислений в различных приложениях, включая научные расчеты, финансовый анализ и графику. Правила IEEE 754 включают спецификации для различных форматов представления чисел, таких как одинарная и двойная точность, а также определяют правила округления и обработки исключительных значений. Применение стандартов IEEE 754 помогает избежать ошибок при вычислениях и обеспечивает согласованность результатов на различных платформах.

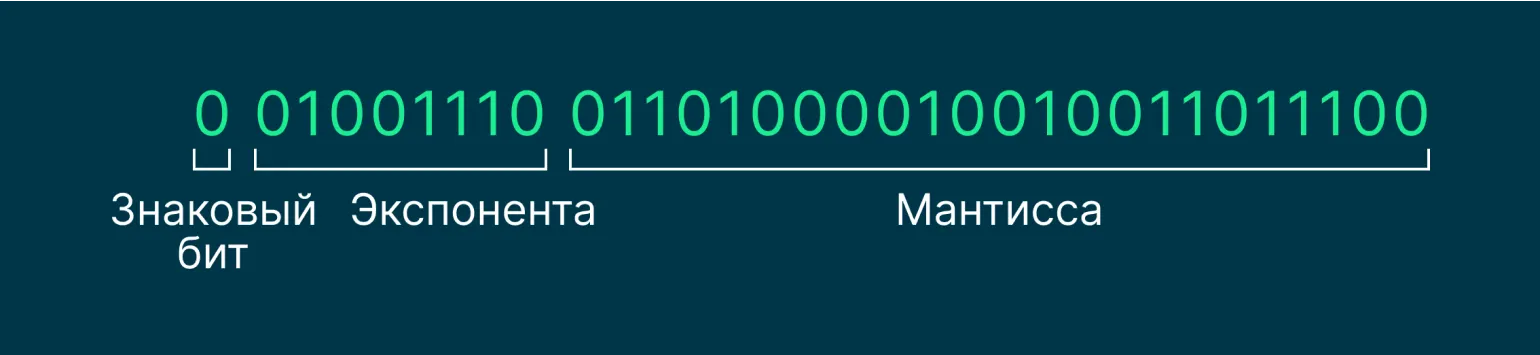
В соответствии с стандартом IEEE 754 числа представляются фиксированным количеством битов, каждый из которых выполняет свою уникальную функцию. В стандартной реализации используется 32 бита, которые делятся на три основных компонента: один бит предназначен для обозначения знака числа, 8 бит отводится для экспоненты, а 23 бита используются для мантиссы. Этот формат позволяет эффективно представлять как целые, так и дробные числа, обеспечивая точность и диапазон значений в вычислениях. Стандарт IEEE 754 играет ключевую роль в компьютерной арифметике и широко применяется в современных процессорах и программном обеспечении.

Знаки, экспоненты и мантиссы являются ключевыми элементами в представлении чисел с плавающей запятой. Знаковый бит указывает, является ли число положительным или отрицательным. Экспонента отвечает за масштабирование величины, позволяя представлять как очень большие, так и очень маленькие числа. Мантисса, в свою очередь, определяет точность представления значения, обеспечивая необходимый уровень детализации. Правильное понимание этих компонентов важно для работы с числовыми данными в вычислениях и программировании.

Для преобразования двоичного числа в десятичное используется определенная формула. Каждая цифра двоичного числа умножается на 2 в степени ее позиции, начиная с нуля справа. Затем все полученные значения суммируются. Это позволяет получить эквивалентное десятичное число. Например, чтобы преобразовать двоичное число 1011 в десятичное, нужно вычислить: 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0, что в итоге дает 11 в десятичной системе. Применение этой формулы позволяет легко и быстро выполнять конвертацию между двоичной и десятичной системами счисления.

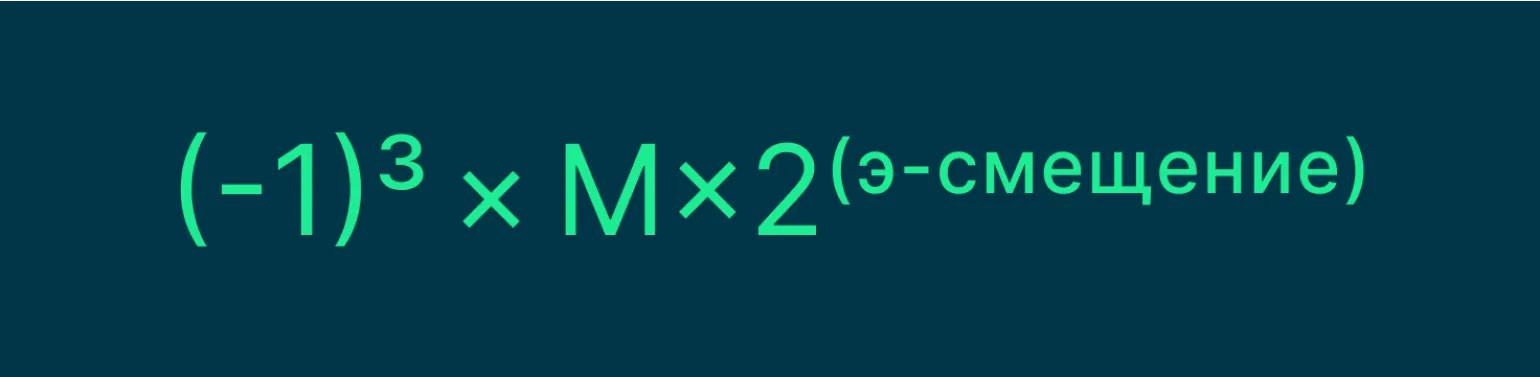
В данной формуле З обозначает знаковый бит, М представляет мантиссу, а Э — экспоненту. Для корректного отображения как положительных, так и отрицательных значений экспоненты применяется смещение, равное 127. Это смещение позволяет упростить работу с числами, обеспечивая более удобное представление в двоичной системе. Таким образом, использование знакового бита и смещения делает возможным эффективное представление чисел с плавающей точкой.

В пределах без учета смещения значение экспоненты колеблется от 0 до 255, в то время как с учетом смещения диапазон изменяется от −127 до 128. Это смещение способствует более эффективному представлению малых чисел, что особенно важно в компьютерной графике и цифровой обработке сигналов. Правильное использование форматов представления чисел позволяет оптимизировать память и улучшить производительность вычислений.

Для вычисления мантиссы к числу добавляется единица, после чего размещается десятичная точка, как в числе с фиксированной точкой. После этого производится расчет.

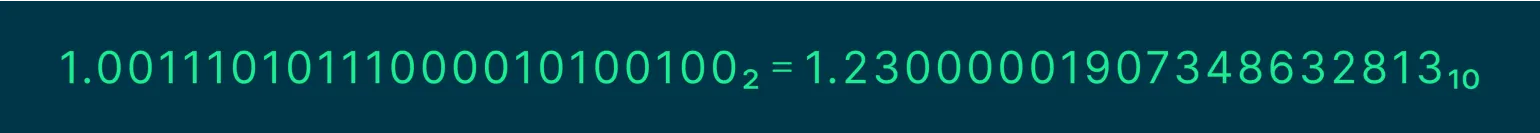
В результате вычислений мы получаем значение 1.23, однако это число является лишь приближением. В идеальных условиях, при наличии бесконечного количества бит, точное значение могло бы быть представлено как 1.2300000000000000000000000000000001, обеспечивая более точное отображение. Тем не менее, из-за ограниченной битовой длины в цифровых вычислениях происходит округление, что влияет на точность представления чисел. Это явление важно учитывать при работе с высокоточными вычислениями и в задачах, требующих высокой степени точности.

Теперь подставим все значения в формулу. Это позволит нам получить точный результат и проанализировать все параметры. Важно учитывать каждую переменную, чтобы обеспечить правильность расчетов и избежать ошибок. Подробное внимание к каждому элементу формулы поможет нам достичь наилучших результатов и глубже понять процесс.

Все вычисления подтверждаются. Теперь давайте преобразуем другое двоичное число в десятичную систему. Рассмотрим следующее двоичное представление:

Оптимизация текста для SEO заключается в использовании ключевых слов и фраз, которые помогут улучшить видимость контента в поисковых системах. Важно также сделать текст более информативным и привлекательным для читателей.

Текущий текст «0 10000000 11100000000000000000000» не содержит информативного содержания и не подходит для SEO. Рекомендуется добавить контекст и объяснить, что обозначают эти цифры. Например, если это относится к числовым данным, их можно представить как статистику, графики или другие аналитические показатели.

Следующий вариант текста может звучать так:

«В современных аналитических системах часто используются числовые данные для визуализации информации. К примеру, значения 0, 10,000,000 и 111,000,000,000,000,000,000 могут представлять собой различные категории статистики или финансовые показатели. Эти данные имеют большое значение для анализа трендов и принятия обоснованных решений. Понимание числовых показателей позволяет лучше ориентироваться в объемах, тенденциях и возможностях на рынке.»

Такой подход не только улучшает SEO, но и делает текст более полезным для аудитории.

Мы будем следовать всем необходимым этапам.

• знаковый бит — 0;
• экспонента — 128;
• мантисса — 1.875.

Теперь необходимо подставить полученные значения в формулу. Это позволит нам провести анализ и получить нужный результат. Применение формулы с актуальными данными поможет точно определить искомые параметры и упростить дальнейшие вычисления. Важно следить за правильностью всех значений, чтобы избежать ошибок и получить достоверный итог.

В результате вычислений мы получаем десятичное значение 3.75. Это значение может быть использовано в различных математических задачах и приложениях, требующих точности.

Понимание особенностей чисел с плавающей точкой

Числа с плавающей точкой играют ключевую роль в вычислительных системах. Мы уже обсудили, как они хранятся в памяти и преобразуются в десятичные значения согласно стандарту IEEE 754. Теперь углубимся в их характеристики и особенности использования. Числа с плавающей точкой позволяют выполнять точные математические операции, которые необходимы в науке, инженерии и финансовых приложениях. Однако, несмотря на их преимущества, важно учитывать возможные ошибки округления и ограничения точности при работе с такими числами. Понимание этих аспектов поможет избежать проблем и обеспечить корректные вычисления в различных программных приложениях.

В области чисел с плавающей точкой встречаются уникальные значения, такие как положительный и отрицательный ноль, положительная и отрицательная бесконечности, а также неопределённость. Эти концепции играют ключевую роль в обеспечении точности вычислений и в правильной интерпретации результатов. Понимание этих значений помогает разработчикам и исследователям избегать ошибок и повышает эффективность работы с данными в различных приложениях, включая научные вычисления и финансовый анализ.

Положительный и отрицательный нули играют важную роль в вычислениях на компьютерах, позволяя различать значения, близкие к нулю, но имеющие разные знаки. Это особенно актуально в финансовых приложениях, где работа с малыми процентными ставками требует четкого понимания, является ли ставка положительной или отрицательной. Учет этих различий способствует более точному анализу данных и принятию обоснованных решений в финансовой сфере.

Отсутствие двух нулей в числовых вычислениях может вызвать значительные ошибки при округлении. В соответствии со стандартом IEEE 754, эти нули представлены следующим образом:

Бесконечность в математике делится на два типа: положительную и отрицательную. Деление на ноль приводит к бесконечности, и хотя эта идея может показаться необычной, она играет ключевую роль в различных математических концепциях и теориях. Понимание бесконечности необходимо для исследования пределов, функций и числовых рядов, что делает эту тематику особенно важной для студентов и специалистов в области математики.

Положительная бесконечность возникает, когда положительное число делится на ноль, который имеет положительный знак, в то время как отрицательная бесконечность возникает при делении отрицательного числа на положительный ноль. Это можно объяснить следующим образом: когда мы пытаемся разделить положительное число на все меньшие значения, приближающиеся к нулю, результат стремится к положительной бесконечности. Аналогично, деление отрицательного числа на значения, стремящиеся к положительному нулю, приводит к отрицательной бесконечности. Таким образом, концепции положительной и отрицательной бесконечности связаны с поведением функций и пределов в математике.

В двоичном представлении положительной бесконечности экспонента заполняется только единицами, а мантисса состоит исключительно из нулей. Аналогичная ситуация наблюдается и для отрицательной бесконечности. Это свойство важно учитывать при работе с числами в формате с плавающей запятой и при анализе особенностей представления бесконечности в вычислительных системах.

Неопределённость, известная как Not-a-Number (NaN), проявляется в ситуациях, когда результат математической операции нельзя точно определить. Одним из распространённых примеров является деление нуля на ноль. Неопределённость обладает особыми свойствами, которые важно учитывать при работе с числами в программировании и вычислениях. Например, NaN не равен ни одному числу, включая самого себя, что может привести к неожиданным результатам при сравнении. Понимание и правильная обработка NaN критически важны для предотвращения ошибок в алгоритмах и вычислениях.

Главное отличие NaN (Not a Number) от бесконечности заключается в том, что в NaN присутствует хотя бы один ненулевой бит в мантиссе. Это означает, что NaN используется для обозначения неопределенных или недопустимых числовых значений, в то время как бесконечность представляет собой числовое значение, выходящее за пределы конечных значений. Понимание этих различий важно для работы с числовыми данными и вычислениями в программировании и математике. NaN может возникать в результате деления на ноль, недопустимых операций или ошибок в вычислениях, тогда как бесконечность может возникнуть в результате превышения пределов числовых типов. Знание этих аспектов помогает разработчикам правильно обрабатывать исключительные случаи и избегать ошибок в коде.

Стандарт IEEE 754 определяет две основные категории чисел с плавающей точкой: нормализованные и денормализованные. Нормализованные числа используются для представления больших значений и обеспечивают высокую точность при вычислениях. Денормализованные числа, в свою очередь, служат для представления очень малых значений, которые близки к нулю. Этот стандарт является основополагающим для работы с числами с плавающей запятой в современных вычислительных системах, обеспечивая надежность и согласованность числовых представлений.

Нормализованные числа обеспечивают высокую точность и требуют меньше памяти для хранения по сравнению с другими форматами. В научной нотации число 123 представляется как 1.23 × 10². Такой подход позволяет эффективно использовать память, так как первый бит мантиссы всегда равен единице. Это делает нормализованные числа особенно полезными в вычислительной математике и программировании, где важна не только точность, но и оптимизация использования ресурсов.

Если значение близко к нулю, его можно округлить до нуля, что делает процесс нормализации неэффективным для небольших чисел. Это ограничение следует учитывать при обработке данных, так как малые значения могут потерять свою значимость и не отразить истинную картину. Важно находить баланс при нормализации, чтобы сохранить информативность данных, особенно в случаях, когда малые значения могут иметь значение для анализа.

Денормализованные числа служат эффективным решением для проблемы округления в вычислениях. Однако их использование требует большего количества битов для хранения, что может привести к потерям точности. Важно учитывать эти аспекты при выборе формата чисел для выполнения арифметических операций, особенно в задачах, где критична высокая точность расчетов.

Граница между нормализованными и денормализованными числами устанавливается на уровне 0.75. Этот порог играет ключевую роль в различных областях, включая статистику и анализ данных, так как он определяет, как следует обрабатывать и интерпретировать числовые значения для достижения наилучших результатов. Понимание этого предела позволяет специалистам более эффективно управлять данными и принимать обоснованные решения на основе полученных результатов.

Стандарт одинарной точности для чисел с плавающей точкой использует 32 бита: один бит отводится для знака, восемь бит — для экспоненты, а 23 бита предназначены для мантиссы. Этот формат является наиболее распространенным для представления чисел в вычислениях, обеспечивая баланс между диапазоном значений и точностью. Одинарная точность позволяет эффективно хранить и обрабатывать данные в различных приложениях, включая научные расчеты и графику.

Числа с двойной точностью применяют 64 бита, что обеспечивает значительно более широкий диапазон значений и повышенную точность по сравнению с числами одинарной точности. Это делает их идеальными для использования в приложениях, где необходима высокая степень точности, таких как научные расчеты и инженерные задачи. Использование 64-битных чисел позволяет избежать ошибок округления и обеспечивает более надежные результаты в критически важных вычислениях.

Числа с одинарной точностью могут представлять значения в диапазоне от −3.40282347 × 10³⁸ до +3.40282347 × 10³⁸, обеспечивая точность до семи знаков после запятой. В свою очередь, числа с двойной точностью имеют более широкий диапазон, который варьируется от −1.7976931348623157 × 10³⁸ до +1.7976931348623157 × 10³⁸ и гарантируют точность от 15 до 17 знаков после запятой. Эти характеристики делают числа с одинарной и двойной точностью важными для вычислений в программировании и научных расчетах, где необходима высокая степень точности.

В языках программирования, включая Java, имеются специализированные типы данных, такие как BigInteger и BigDecimal, которые предназначены для работы с числами произвольной точности. Хотя эти типы данных обеспечивают высокую точность вычислений, их использование может негативно влиять на производительность приложений. Это связано с тем, что операции с большими числами требуют больше времени на обработку и потребляют больше ресурсов. Поэтому разработчикам следует тщательно обдумывать, когда и как применять BigInteger и BigDecimal, чтобы сбалансировать между необходимостью точности и эффективностью работы программного обеспечения.

Ключевые моменты для усвоения

В этой статье мы подробно исследовали концепцию чисел с плавающей точкой. Тем не менее, это только поверхностное знакомство с широкой и сложной темой, которая требует глубокого анализа и понимания. Изучение чисел с плавающей точкой может занять много времени, но знание основных принципов и особенностей этой концепции является крайне важным. В заключение мы выделим ключевые моменты, которые стоит запомнить для будущего использования.

• Числа с плавающей точкой представляют собой приближённое отображение вещественных чисел в программировании, и все правила их представления основаны на стандарте IEEE 754.
• Данный стандарт необходим для обеспечения совместимости и эффективности работы с вещественными числами на различных компьютерных архитектурах.
• Существуют два основных формата чисел с плавающей точкой: одинарная и двойная точность. Одинарная точность занимает 32 бита и включает один знак, восемь бит для экспоненты и 23 бита для мантиссы. В то время как двойная точность использует 64 бита: один знак, 11 бит для экспоненты и 52 бита для мантиссы.
• Стандарт IEEE 754 также включает специальные значения, необходимые для представления положительного и отрицательного нуля, бесконечностей и неопределённых значений.

Если вы хотите узнать больше увлекательного контента, присоединяйтесь к нашему телеграм-каналу. Мы регулярно публикуем свежие материалы, которые помогут вам оставаться в курсе самых актуальных тем. Не упустите возможность быть частью нашего сообщества и получать интересные обновления прямо на свой телефон.

В дополнение к основному материалу, мы рекомендуем вам ознакомиться с следующими ресурсами. Это поможет вам углубить свои знания и получить более полное представление по теме. Наши рекомендации включают статьи, исследования и практические руководства, которые позволят вам расширить горизонты и повысить свою экспертизу в данной области. Не упустите возможность обогатить свои знания и улучшить навыки, изучая предложенные материалы.

• Как подготовиться к собеседованию: случайные числа в Python
• Тест на знание эзотерических языков программирования
• Двоичная арифметика: основные операции с бинарными числами