Код #Статьи

30 мая, 2025

Теория игр: 5 основных понятий для новичков

Изучите ключевые аспекты теории игр и применяйте их каждый день.

Содержание:

Понимание теории игр: ключ к анализу стратегий
Что такое игра: Понимание и основы
Что такое стратегия в теории игр?
Дилемма заключённого: Основы теории игр
Разнообразие игровых жанров: основные типы игр
Применение теории игр в различных сферах
Рекомендации для изучения теории игр

Заработок в IT: 5 способов быстро начать в 2025 году

Узнать больше

Понимание теории игр: ключ к анализу стратегий

Теория игр представляет собой математическую дисциплину, исследующую взаимодействие участников в условиях конкуренции. Под «игрой» понимается ситуация, в которой интересы как минимум двух сторон находятся в конфликте. Это может быть как классическая шахматная партия, так и более сложные сценарии, например, выборы президентов или виртуальные сражения в игре Fortnite. Теория игр находит применение в различных областях, включая экономику, политологию и социологию, позволяя анализировать стратегии и прогнозировать поведение участников. Это делает её важным инструментом для понимания сложных систем и принятия решений в конкурентной среде.

Теория игр фокусируется на изучении взаимодействий между игроками и их стратегиями, а также на том, как решения одного участника могут повлиять на действия других. Ярким примером этого может служить утренний час пик, когда выбор маршрута и времени выезда одного водителя оказывает значительное влияние на движение и комфорт других участников дорожного движения. В таких ситуациях каждый водитель должен учитывать не только свои интересы, но и возможные действия других, что делает теорию игр важным инструментом для анализа коллективного поведения в различных ситуациях.

Представьте, что вы просыпаетесь и понимаете, что опаздываете на работу. Вам необходимо как можно быстрее добраться до офиса, но в такой же ситуации находятся ещё 200 тысяч жителей вашего района. Каждый из них выбирает один из привычных способов передвижения: метро, автобус, такси или личный автомобиль. В результате улицы и общественный транспорт переполнены, а время в пути значительно увеличивается. Чтобы избежать подобных ситуаций, стоит заранее планировать свой маршрут и рассмотреть альтернативные способы передвижения. Оптимизация времени поездки поможет не только избежать стресса, но и повысить продуктивность на работе.

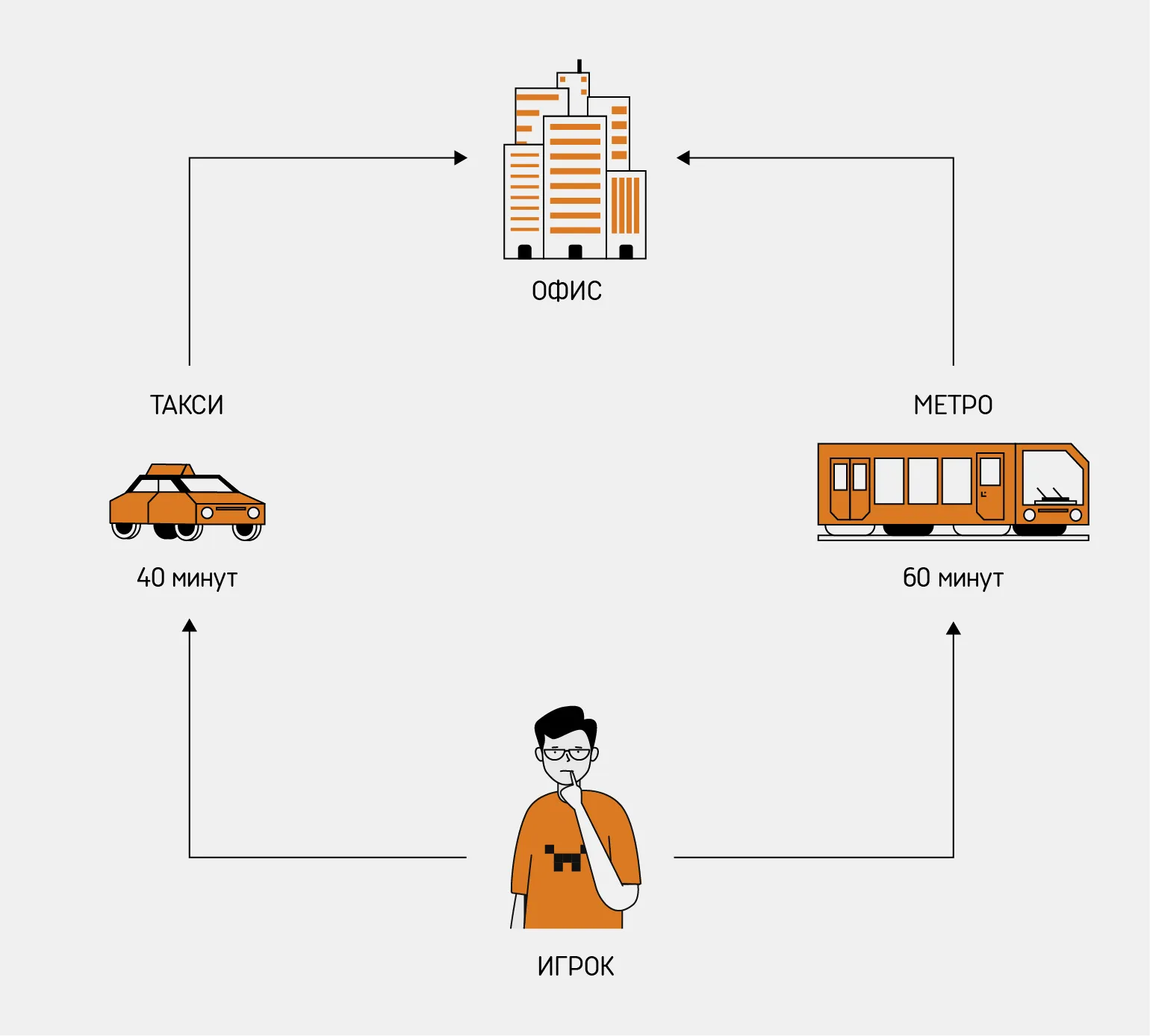
Игрок имеет возможность выбрать разные стратегии, каждая из которых приведёт к различным результатам. Иллюстрация: Оля Ежак для Skillbox Media

С точки зрения теории игр, вы и ваши соседи являетесь игроками, объединёнными общей целью — быстро достичь нужной точки. Ваш успех зависит не только от собственных решений, но и от действий других участников. Каждый выбор, который вы делаете, влияет на общий результат, что делает взаимодействие между игроками ключевым аспектом в этой ситуации. Важно учитывать не только свои интересы, но и стратегию соседей, чтобы оптимизировать собственный маршрут и минимизировать время в пути.

Когда вы планируете поездку на такси, вы можете рассчитывать на 40 минут в пути. Однако, если многие другие пассажиры выберут тот же маршрут, вы рискуете столкнуться с пробками, что значительно увеличит время в пути. Кроме того, рост спроса на такси может привести к повышению тарифов, что также стоит учитывать при планировании поездки. Чтобы избежать неприятных сюрпризов, рекомендуется заранее проверять текущую ситуацию на дорогах и возможные альтернативные маршруты.

Представьте, что вы планируете воспользоваться метро. Вы понимаете, что это займет примерно 35 минут, к которым добавится еще 25 минут на дорогу до станции и спуск по эскалатору. Однако, если большинство горожан также выберут этот способ передвижения, вас ожидают следующие сложности: увеличенное время ожидания, переполненные вагоны и возможные задержки в движении. Это может существенно повлиять на вашу общую поездку и время в пути. Чтобы избежать неудобств, стоит рассмотреть альтернативные варианты транспортировки, такие как автобусы, такси или даже велосипед.

пробки на пути к метро;
очереди на кассах и эскалаторах;
переполненные платформы, из-за которых вы можете пропустить несколько поездов.

Чтобы победить в данной игре, необходимо предугадать действия других участников и выбрать оптимальное решение, которое учитывает все возможные сценарии. Это и есть суть теории игр, которая изучает стратегии взаимодействия между индивидуумами или группами в условиях неопределенности. Теория игр помогает анализировать различные ситуации, позволяя игрокам принимать обоснованные решения и повышать свои шансы на успех.

Аренда самоката представляет собой один из самых эффективных способов передвижения в городе. Несмотря на возможные ветер и пыль, вы сможете добраться до места назначения всего за 50 минут, избегая пробок и очередей. Летний сезон и новые велодорожки делают аренду самоката особенно актуальной и удобной. Этот экологически чистый и экономичный способ передвижения позволяет наслаждаться городским пейзажем, а также способствует активному образу жизни.

Что такое игра: Понимание и основы

Игра представляет собой не просто форму досуга, а сложную систему взаимодействия, в которой интересы участников могут пересекаться и конфликтовать. У каждого игрока есть своя цель, и выбор его действий напрямую влияет на результаты других участников. Важным аспектом игрового процесса являются четко установленные правила, которые должны быть известны всем игрокам. Это создает справедливую и предсказуемую среду, в которой каждый участник может проявить свои стратегии и навыки. Игровой процесс становится более захватывающим благодаря взаимодействию и динамике, возникающим из конфликтов интересов, что делает игры уникальным и увлекательным опытом.

Рассмотрим на примере популярной королевской битвы Fortnite, где в одном матче участвует до 100 игроков, каждый из которых стремится стать последним выжившим. Конфликт интересов в таком формате очевиден — невозможно, чтобы все стали победителями. Игрокам необходимо разрабатывать стратегии, чтобы эффективно нейтрализовать противников и увеличить свои шансы на успех. Важнейшими аспектами являются выбор места высадки, сбор ресурсов и умение адаптироваться к меняющимся условиям игры. Успех в Fortnite зависит не только от мастерства стрельбы, но и от умения планировать тактические действия в условиях высокой конкуренции.

Неудачные действия могут привести к фиаско. Анимация: Fortnite / GIPHY

В этой статье мы рассмотрим ключевые компоненты игры на примере Fortnite и выделим шесть основных элементов, формирующих игровую динамику. Fortnite, как одна из самых популярных игр в жанре королевской битвы, демонстрирует, как различные элементы влияют на игровой процесс и взаимодействие пользователей. Мы проанализируем механики, которые обеспечивают уникальный опыт и привлекают игроков по всему миру. Эти элементы включают в себя построение, стрельбу, исследование, взаимодействие с окружающей средой, командную работу и прогрессию персонажа. Понимание этих компонентов поможет глубже оценить, что делает Fortnite такой увлекательной и динамичной игрой.

Игроки: максимальное количество участников в каждом матче Fortnite достигает 100 человек.
Цель: основная задача — остаться последним выжившим.
Правила: игроки начинают без оружия и должны находить ресурсы, в то время как карта сужается, принуждая к конфликту.
Действия: помимо стрельбы, игроки могут строить структуры, собирать ресурсы и перемещаться по карте.
Информация: игроки могут наблюдать за действиями других, что влияет на их собственные решения.
Взаимозависимость решений: постройка башни может стать сигналом для других игроков — она может привлечь противников или, наоборот, отпугнуть их.

Теория игр значительно шире, чем просто сфера компьютерных игр. Она охватывает разнообразные аспекты жизни, где возникают конфликты интересов. Это может включать в себя выбор фильма для совместного просмотра с друзьями или ведение переговоров о скидке на платформе «Авито». Понимание механик теории игр позволяет глубже осознавать процессы принятия решений в повседневной жизни и улучшать навыки взаимодействия с другими. Используя принципы теории игр, можно научиться более эффективно анализировать ситуации, что способствует достижению лучших результатов как в личных, так и в профессиональных отношениях.

Что такое стратегия в теории игр?

Стратегия представляет собой не просто набор действий, а тщательно продуманный план, который учитывает все возможные обстоятельства в игре. В теории игр каждое действие может привести к различным результатам, и не всегда к тем, которые мы хотим получить. В связи с этим оптимизация своих действий становится ключевым аспектом достижения максимального успеха. Правильный подход к разработке стратегии позволяет минимизировать риски и повысить вероятность положительных исходов, что является важным фактором в любом игровом процессе.

Исследования в области теории игр показывают, что успешные стратегии формируются на основе анализа ресурсов игрока и предсказания возможных действий соперников. Главная цель большинства стратегий заключается в максимизации выигрыша. Без этого мотивации для начала игры не существует. Разработка эффективной стратегии требует глубокого понимания как собственных возможностей, так и вероятных шагов противника.

Выигрыш в игре напрямую зависит от качества принятых решений. Игроки, которые принимают обдуманные и стратегически выверенные решения, могут рассчитывать на значительный успех. В то же время неудачные выборы могут привести к минимальным результатам или даже полной неудаче. Поэтому развитие навыков принятия решений является ключевым аспектом для достижения высоких результатов в любой игре.

Рассмотрим практический пример из шахмат: если вы пожертвуете своего ферзя без четкой необходимости, это не будет оптимальной стратегией. Гораздо разумнее сосредоточиться на атаке фигур противника с целью поставить мат королю. Даже в случае потери ферзя у вас остается возможность продвинуть пешку до конца доски, что позволит вернуть фигуру. Такой подход демонстрирует более эффективное использование ресурсов и стратегическое мышление в игре.

Стратегии в теории игр делятся на четыре основных типа, исходя из целей и ресурсов игроков, а также учитывая действия соперников. Эти классификации помогают глубже понять динамику взаимодействия между участниками и оптимизировать их подходы в различных игровых ситуациях. Правильный выбор стратегии может существенно повлиять на исход игры и повысить шансы на успех.

Чистая стратегия — игрок точно знает, как будет действовать дальше.
Смешанная стратегия — выбор одной из чистых стратегий основывается на вероятности различных исходов.
Доминирующая стратегия — всегда приводит игрока к наилучшему результату, независимо от действий противников.
Компромиссная стратегия — используется в случаях, когда нет ясного выигрыша или проигрыша, позволяя игрокам находить взаимовыгодные решения.

Для более глубокого понимания влияния выбора стратегии на конечные результаты рассмотрим классический пример из теории игр — дилемму заключённого. Этот пример наглядно демонстрирует, как индивидуальные решения участников могут существенно повлиять на общий итог. В дилемме заключённого каждый из двух заключённых должен решить, сотрудничать с партнёром или предать его, что в конечном итоге определяет, насколько хорошими будут результаты для обоих. Это иллюстрирует, как стратегические выборы влияют на общую выгоду и подчеркивает важность анализа взаимодействий в различных ситуациях.

Дилемма заключённого: Основы теории игр

Дилемма заключённого представляет собой классическую ситуацию в теории игр, которая иллюстрирует, как рациональные игроки могут поступать вопреки собственным интересам. В этом сценарии два преступника, находясь в изоляции, сталкиваются с важным выбором, от которого зависит их судьба. Каждый из них может либо сотрудничать с другим, либо предать его. Оптимальный выбор для каждого в отдельности — предательство, однако, если оба выберут этот путь, они окажутся в худшем положении, чем если бы решили сотрудничать. Эта модель подчеркивает сложности принятия решений в условиях неопределенности и конкуренции, что делает её важной для понимания конфликтов и сотрудничества в различных сферах, включая экономику и социальные науки.

Два подозреваемых задержаны и помещены в разные камеры. У следствия имеется достаточное количество улик для предъявления обвинений по менее серьезным правонарушениям, однако доказательства для более тяжкого преступления отсутствуют. Эта ситуация создает напряжение, так как каждый из подозреваемых может попытаться использовать информацию о другом, чтобы улучшить свою позицию. На данном этапе важно, как следствие будет вести допросы и анализировать поведение задержанных, чтобы выявить возможные противоречия в их показаниях и собрать дополнительные доказательства.

Следствие предлагает преступникам определенные условия для заключения сделки. Эти условия направлены на упрощение процесса расследования и могут включать в себя сотрудничество с правоохранительными органами, предоставление информации о других преступниках или преступлениях, а также смягчение наказания в обмен на это сотрудничество. Такие сделки могут быть выгодны как для следствия, так и для обвиняемых, так как позволяют раскрыть более сложные дела и снизить сроки наказания для тех, кто готов сотрудничать. Важно отметить, что подобные условия оговариваются индивидуально и зависят от серьезности преступления и уровня сотрудничества.

Если оба преступника сохранят молчание, они получат по 2 года за незначительное преступление.
Если один из них выдаст другого, а второй останется молчаливым, первый выйдет на свободу, а второй получит 10 лет.
Если оба преступника сдадут друг друга, они получат по 5 лет — больше, чем в случае молчания, но меньше, чем максимальный срок.

Оптимальной стратегией может показаться молчание. Тем не менее, отсутствие общения между игроками приводит к неопределенности: один из участников может получить 10 лет тюрьмы, если другой решит сотрудничать с властями. Таким образом, молчание может обернуться серьезными последствиями для обоих. Важно учитывать риски и последствия каждого выбора, чтобы избежать катастрофических результатов.

Рациональным подходом в данной ситуации является сотрудничество с следствием, что в теории игр обозначается как доминирующая стратегия. В этом случае преступник имеет возможность либо выйти на свободу, либо получить срок в 5 лет, что является значительным преимуществом по сравнению с 10 годами заключения. Сотрудничество может помочь снизить наказание и улучшить исход ситуации.

Игру можно представить как платежную матрицу, отражающую результаты для каждого участника в зависимости от их действий. Этот подход позволяет не только визуализировать, но и математически анализировать игровую ситуацию. Платежная матрица служит эффективным инструментом для понимания стратегий игроков и предсказания исходов в различных сценариях.

Равновесие Нэша — это ситуация в теории игр, когда игроки выбирают стратегии, которые уравновешивают интересы друг друга. Это понятие было разработано Джоном Нэшем и стало основой для современной теории игр. Ключевым моментом равновесия Нэша является то, что игроки могут выбирать стратегии, которые оптимальны для всех участников, хотя при этом выигрыши могут быть не максимальными. Это явление иллюстрирует, как индивидуальные решения игроков влияют на общий результат и подчеркивает важность взаимодействия в конкурентных ситуациях. Понимание равновесия Нэша помогает анализировать различные сценарии в экономике, политике и других областях, где принимаются решения в условиях неопределенности.

Равновесие Нэша акцентирует внимание на значении выбора стратегии, которая обеспечивает выгоду, даже в условиях неопределенности поведения оппонента. Этот концепт демонстрирует, что в некоторых случаях эгоистичные действия могут привести к более выгодным результатам для всех участников. Понимание равновесия Нэша является ключевым для анализа стратегий в различных областях, таких как экономика, политика и игры. Это подчеркивает необходимость тщательного планирования и предвидения возможных ходов соперников для достижения оптимального результата.

Разнообразие игровых жанров: основные типы игр

Изучение теории игр позволяет глубже понять разнообразие игровых форматов. В этой статье мы подробно рассмотрим десять основных типов игр, которые влияют на нашу игровую реальность. Каждый из этих типов имеет свои уникальные особенности и стратегии, которые определяют, как игроки взаимодействуют друг с другом и с игровым миром. Понимание этих категорий поможет не только улучшить навыки игры, но и расширить горизонты в области разработки и анализа игр.

Кооперативные и некооперативные игры представляют собой две основные категории игрового процесса. В кооперативных играх участники работают вместе для достижения общих целей. Ярким примером такой игры является популярная Minecraft, в которой игроки исследуют мир, строят совместные сооружения и помогают друг другу в выполнении задач. В отличие от кооперативных, некооперативные игры, такие как автогонки или шахматы, сосредотачиваются на конкуренции, где каждый игрок стремится одержать победу самостоятельно. Эти два типа игр привлекают разные аудитории и предлагают уникальный опыт взаимодействия.

Игры с нулевой и ненулевой суммой представляют собой две основные категории в теории игр. Игры с нулевой суммой характеризуются тем, что выигрыш одного игрока непосредственно соответствует проигрышу другого. Примеры таких игр включают покер и спортивные соревнования на выбытие, где один участник получает всё, а другие остаются ни с чем. В отличие от них, игры с ненулевой суммой позволяют игрокам делить выигрыши. В стратегических играх, таких как Civilization или Mount & Blade 2, участники могут достигать различных результатов, что позволяет некоторым игрокам получать больше, чем другие. Эти различия в типах игр важны для понимания стратегий и динамики взаимодействия между игроками.

Параллельные и последовательные игры представляют собой две основные категории в теории игр. В параллельных играх, таких как «Мафия» или дилемма заключённого, участники принимают решения одновременно или не осведомлены о действиях соперников до завершения своего хода. Это создает уникальную динамику, где важна способность предугадывать действия других игроков. В отличие от них, последовательные игры, например, шахматы, требуют от участников поочередного выполнения ходов. В таких играх необходимо разрабатывать стратегию и предвидеть возможные действия соперника, что делает каждое решение критически важным для достижения победы. Понимание различий между параллельными и последовательными играми помогает игрокам адаптировать свои стратегии и повышать эффективность в различных игровых ситуациях.

Игры с полной и неполной информацией имеют свои уникальные особенности и стратегии. В играх с полной информацией, таких как шахматы, каждый игрок обладает полным знанием о возможных ходах и состоянии игры. Это создает условия для глубокого анализа и предсказания действий соперника. В противоположность этому, игры с неполной информацией, например, популярные онлайн-шутеры CS:GO и Call of Duty: Warzone, предлагают ограниченное понимание действий противника. Это добавляет элемент неожиданности и требует от игроков быстрой адаптации и стратегического мышления. Знание различий между этими типами игр может помочь игрокам лучше развивать свои навыки и подходы к стратегиям.

Симметричные и несимметричные игры являются важными концепциями в теории игр. Симметричные игры, например дилемма заключённого, имеют одинаковые стратегии для всех игроков, и их замена местами не изменяет исход игры. В отличие от этого, несимметричные игры предполагают различия в стратегиях, что создает уникальные условия для каждого участника. Понимание этих типов игр помогает глубже осознать взаимодействие между игроками и предсказать возможные результаты.

Применение теории игр в различных сферах

Теория игр является важным инструментом для анализа и моделирования различных ситуаций, от повседневных до сложных стратегических взаимодействий. Принципы теории игр активно применяются в современных областях, таких как экономика, политика, экология и бизнес. В экономике теории игр помогают понять конкурентное поведение компаний, а в политике — стратегии принятия решений и коалиционного поведения. Экология использует теорию игр для анализа взаимодействий между видами, а в бизнесе — для оптимизации ценовых стратегий и маркетинга. Эти области демонстрируют, как теория игр может помочь в принятии более обоснованных решений и в разработке эффективных стратегий.

Бизнес — здесь теория игр используется для оценки конкурентных действий и формирования эффективных маркетинговых стратегий. Интересно, что конкурентом может выступать даже природа: например, производителю кроссовок необходимо находить пути для поддержания уровня продаж, независимо от погодных условий.
Биология — теория игр помогает исследовать поведение животных, включая аспекты конкуренции и кооперации, которые способствуют выживанию видов. Это позволяет глубже понять, каким образом эволюция формирует оптимальные стратегии для адаптации.
Международные отношения — в этой области теория игр является важнейшим инструментом. Она позволяет прогнозировать последствия политических изменений, таких как смена режима в одной стране и её влияние на соседние государства.
Data Science — в этой сфере теория игр применяется для обучения нейронных сетей, которые взаимодействуют как с людьми, так и с другими искусственными интеллектами. Примером может служить нейросеть от DeepMind, которая научилась играть в «Захват флага» в процессе совместной игры с людьми и другими алгоритмами.
Повседневная жизнь — мы ежедневно сталкиваемся с проявлениями теории игр, часто не осознавая этого. Такие ситуации, как пробки, выбор фильма для просмотра, свидания, совместное воспитание детей и переговоры о повышении зарплаты, могут быть проанализированы с помощью математического моделирования.