Системы счисления: для чего нужны, какие бывают, чем различаются / Skillbox Media

Содержание:

• Основные системы счисления
• Непозиционные системы счисления
• Единичная система счисления
• Древнеегипетская десятичная система
• Римская система счисления
• Греческая и славянская системы счисления
• Позиционные системы счисления
• Смешанные системы счисления
• Перевод из одной системы в другую

Основные системы счисления

Система счисления представляет собой математический язык, позволяющий использовать символы для записи чисел в соответствии с определёнными правилами. Она обеспечивает основу для числовых вычислений и позволяет эффективно представлять и обрабатывать числовую информацию. Существуют различные системы счисления, такие как десятичная, двоичная, восьмеричная и шестнадцатеричная, каждая из которых имеет свои уникальные особенности и области применения. Понимание систем счисления является важным аспектом математики и информатики, что позволяет лучше осваивать алгоритмы и компьютерные технологии.

На протяжении всей истории человечества было разработано множество методов записи чисел, однако в современном мире выделяются два основных типа: натуральные и целые числа. Эти категории чисел играют ключевую роль в математике и повседневной жизни, обеспечивая основу для различных вычислений и финансовых операций. Понимание этих типов чисел важно для решения математических задач и анализа данных, что делает их незаменимыми в учебных заведениях и профессиональной деятельности.

• Непозиционные системы — древнейшие системы счисления, в которых значение символа остаётся неизменным вне зависимости от его места в числе. Например, в римской системе символ X всегда обозначает 10, независимо от того, стоит ли он в начале (XVI = 16) или в конце (LX = 60).
• Позиционные системы — системы счисления, где значение цифры определяется её положением в числе. Например, в числе 333 у каждой тройки разное значение: первая означает 300, вторая — 30, а третья — 3.

Системы счисления имеют различные области применения, что влияет на их использование в повседневной жизни. Позиционные системы, такие как десятичная, удобны для арифметических вычислений, так как позволяют легко выполнять операции сложения и вычитания. Например, сложить числа 23 и 45 гораздо проще, чем XXIII и XLV в римской системе. Непозиционные системы, хотя и менее распространены, находят свое применение в специфических случаях, таких как нумерация глав в книгах (I, II, III) или обозначение веков (например, XX век). Понимание различных систем счисления помогает лучше ориентироваться в математике и истории, что делает их важными для обучения и использования в разных сферах.

В следующих разделах мы подробно рассмотрим непозиционные и позиционные системы счисления. Начнем с анализа непозиционных систем, чтобы понять причины их замены позиционными системами. Затем перейдем к изучению позиционных систем, ознакомимся с их разновидностями и освоим методы конвертации чисел между различными форматами. Это поможет вам лучше понять основы чисел и их представление в различных системах счисления.

Непозиционные системы счисления

Непозиционные системы счисления возникли естественным образом в процессе эволюции человеческого общества. Основными предпосылками их появления стали необходимость учета и обмена, а также ограниченность инструментов для вычислений. Эти системы, не имея фиксированного значения для каждого символа в зависимости от его положения, стали важным этапом в развитии математических понятий. Они сыграли ключевую роль в формировании базовых навыков счета и в дальнейшем способствовали переходу к более сложным позиционным системам.

• Древним цивилизациям требовался надёжный способ учёта товаров, землемерия, строительства и астрономических наблюдений.
• Развитие письменности позволило записывать числовые значения.
• Использование отдельных символов для записи чисел оказалось интуитивно понятным способом счёта.

К числу самых известных непозиционных систем счисления относятся единичная, древнеегипетская, римская, греческая и славянская. В этом тексте мы подробно рассмотрим уникальные характеристики и историческую значимость каждой из этих систем. Непозиционные системы счисления играли важную роль в развитии математики и культурных традиций различных народов, отражая особенности их мышления и восприятия чисел.

Единичная система счисления

Единичная система счисления представляет собой базовый метод записи чисел, при котором количество обозначается многократным повторением одного и того же символа. Эта система счисления возникла естественным образом в процессе подсчета предметов, когда более сложные математические концепции ещё не были разработаны. Единичная система служит основой для понимания чисел и математики, позволяя визуализировать количество объектов. Она иллюстрирует, как люди в древности считали и организовывали информацию, что является важным шагом в развитии числовых систем.

Люди издавна использовали различные символы для обозначения чисел: палочки, камешки, узелки — всё, что было доступно. Эта система применялась в различных областях, начиная от древних методов подсчёта дней с помощью зарубок на дереве или камне и заканчивая современными играми, где она помогает вести счёт. Записать число в этой системе очень легко: например, число 5 обозначается пятью палочками (|||||), а число 3 — тремя палочками (|||). Такие примитивные способы счёта стали основой для более сложных математических систем и демонстрируют эволюцию числового представления в человеческой культуре.

Единичная система была удобна для выполнения простых арифметических операций, таких как сложение и вычитание. Однако при работе с большими числами возрастал риск ошибок как в записи, так и в вычислениях. Например, чтобы записать число 100, потребовалось бы изобразить сто отдельных палочек, что было крайне неудобно. В результате, с развитием цивилизации, люди начали группировать символы, что способствовало созданию более эффективных систем счисления. Эти новые системы позволили значительно упростить вычисления и минимизировать вероятность ошибок, что стало важным шагом в развитии математики и науки.

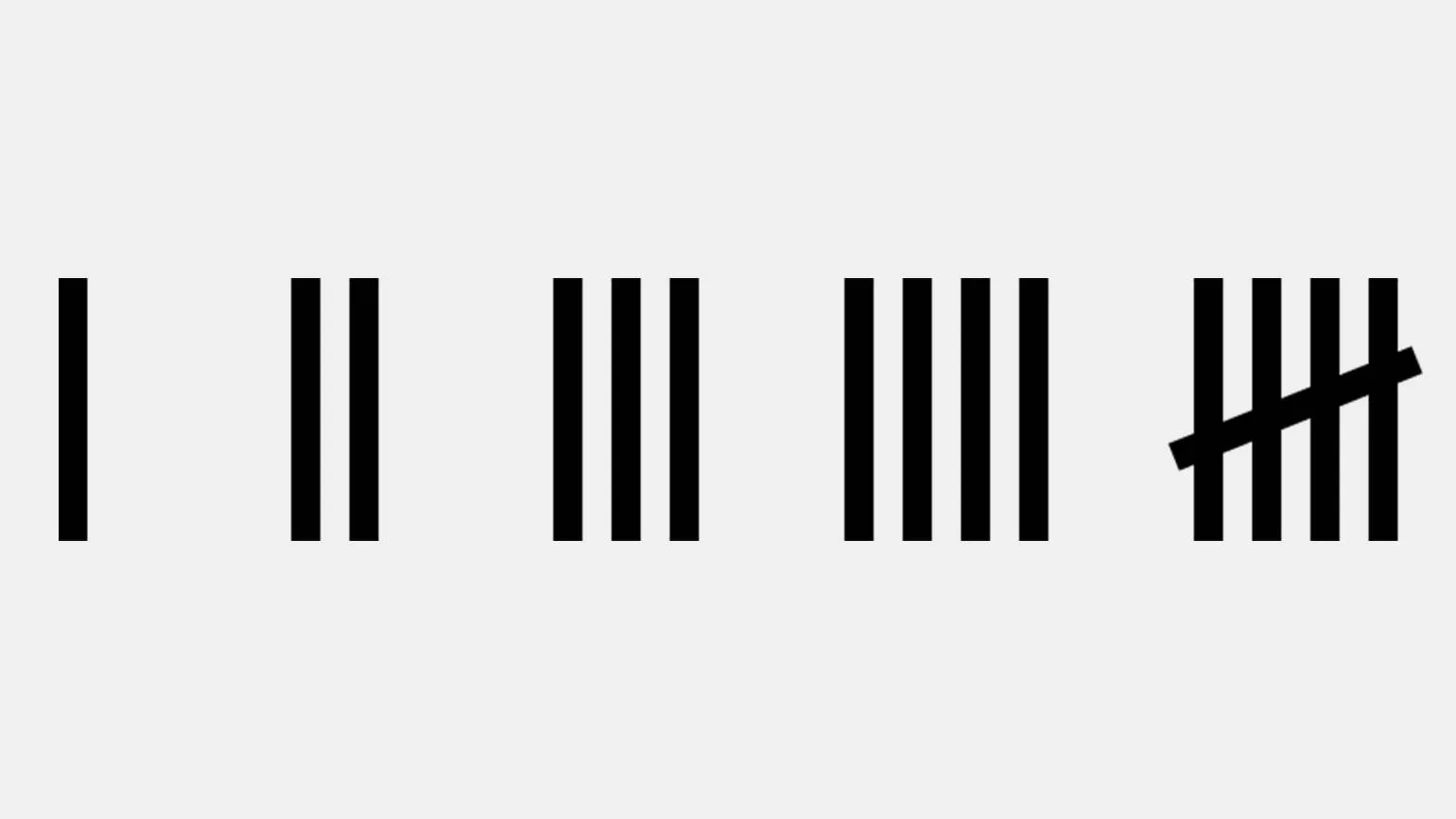
Древнеегипетская десятичная система

Древнеегипетская десятичная система счисления, основанная на числе 10, была важной частью культуры и повседневной жизни древних египтян. Эта система использовалась в различных сферах, включая торговлю, строительство, земледелие и астрономию. Для обозначения чисел применялись уникальные иероглифы: палочка представляла единицу (1), арка соответствовала десятке (10), моток верёвки обозначал сотню (100), водяная лилия — тысячу (1000), согнутый палец символизировал десять тысяч (10 000), лягушка или головастик указывали на сто тысяч (100 000), а человек с поднятыми руками представлял миллион (1 000 000). Эта система позволила древним египтянам эффективно управлять ресурсами и вести учёт, что способствовало их процветанию.

Древние египтяне не уделяли большого внимания направлению записи чисел и могли записывать их слева направо, справа налево или сверху вниз. Учёные выявили, что у них существовал специальный знак, выполнявший функции нуля, который изображался как сердце с трахеей. Этот знак использовался в бухгалтерских папирусах для обозначения полного расхода средств, а также в чертежах для указания уровня земли. Элементы их числовой системы и способы записи чисел отражают уникальный подход к математике и учёту в древнеегипетской культуре.

Египтяне активно применяли дроби в своих расчетах. Они использовали уникальный способ записи, при котором над числом размещали специальный иероглиф, напоминающий рот, который обозначал часть целого. Эта система позволяла эффективно выражать и обрабатывать дробные значения в математике Древнего Египта. Использование дробей было важным аспектом их вычислений, что свидетельствует о высоком уровне математических знаний египетских мудрецов.

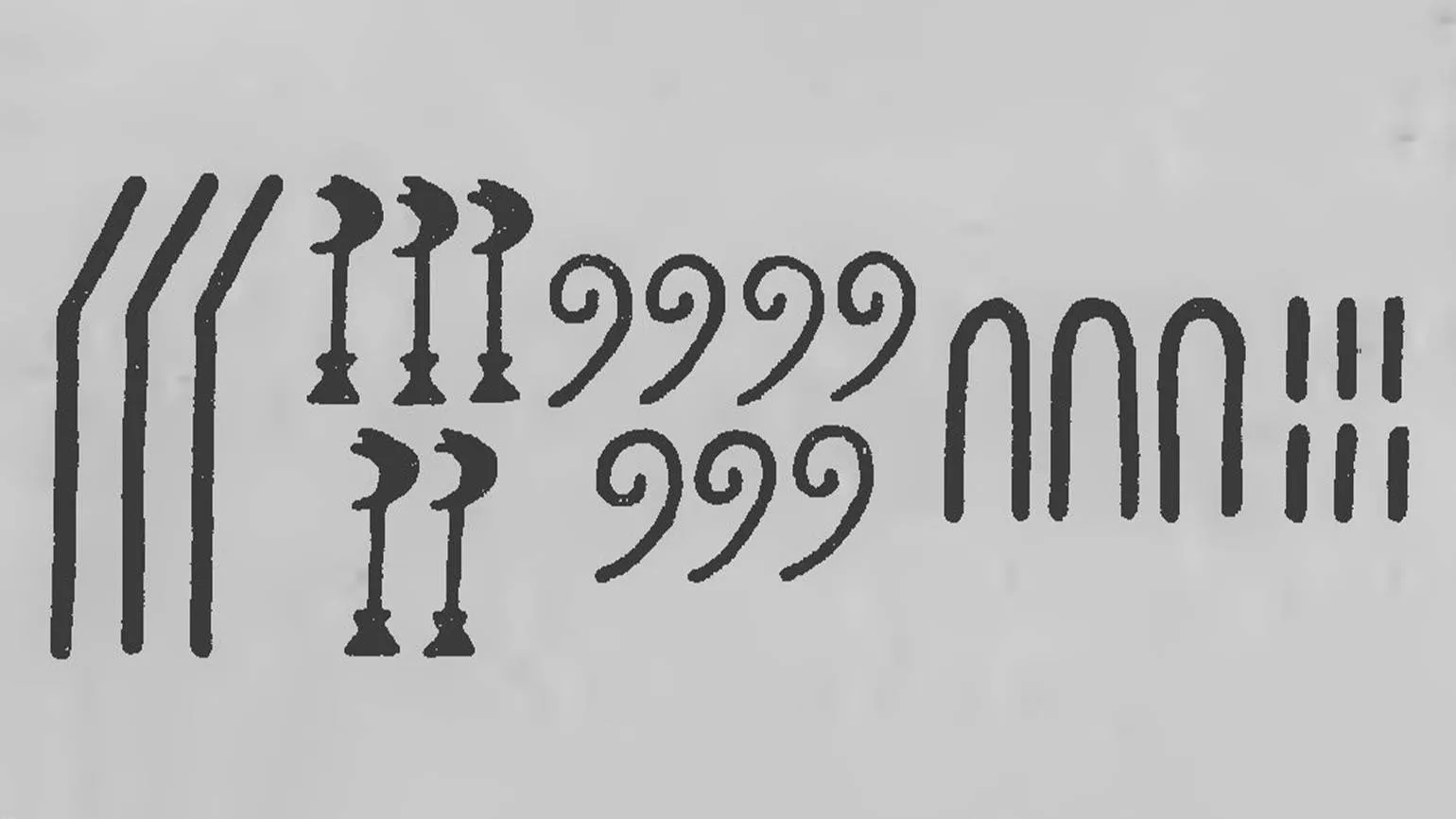
Римская система счисления

Римская система счисления представляет собой метод записи чисел с использованием букв латинского алфавита. Основу этой системы составляют принципы сложения и вычитания значений символов, где каждой букве соответствует определенное число. К числовым символам относятся: I (1), V (5), X (10), L (50), C (100), D (500) и M (1000). Римские цифры применялись в древнем Риме и до сих пор используются в различных сферах, например, для обозначения веков, глав в книгах и на часах. Понимание римской системы счисления полезно для исторического и культурного контекста, а также для решения математических задач.

Каждое число представляет собой последовательность символов, которая записана в соответствии с определёнными правилами. Значение числа формируется из значений всех его символов. Например, число 32 в римской системе обозначается как XXXII, где 30 (XXX) и 2 (II) складываются, чтобы получить итоговое значение 32. Понимание чисел и их символического представления является важным аспектом математики и истории счёта.

Если меньший символ располагается слева от большего, его значение вычитается из значения большего. Например, число 48 представляется как XLVIII: из 50 (L) вычитается 10 (X), затем добавляется 5 (V) и 3 (III). Следует учитывать, что слева от большего символа может находиться только один меньший символ. Это означает, что запись типа XXL недопустима и не может обозначать число 30. Правильное понимание правил записи римских чисел помогает избежать ошибок и обеспечит точность в их использовании.

В современном обществе римские цифры применяются для различных целей, таких как обозначение веков, глав в литературе, часов на циферблатах, а также порядковых номеров монархов и значимых событий. Например, XXI век, глава IV, Карл V, том III и Пётр I. Использование римских цифр придаёт тексту исторический и официальный оттенок, что делает их актуальными и востребованными в различных контекстах.

Греческая и славянская системы счисления

Греческая и славянская системы счисления представляют собой алфавитные методы записи чисел, в которых числовые значения передаются с помощью букв. Греческая система основывается на греческом алфавите, тогда как славянская использует кириллицу. Эти системы широко применялись в религиозных текстах, летописях и деловых документах, что подчеркивает их важность в культуре и истории соответствующих народов. Каждая из систем имеет свои уникальные особенности и правила, что делает их интересными для изучения и анализа в контексте исторической арифметики и лексикографии.

В греческой системе буквы имели числовые значения: «альфа» соответствовала 1, «бета» — 2, а «йота» — 10. В славянской системе буквы также имели свои числовые обозначения: «аз» означала 1, «веди» — 2, а «и десятеричное» — 10. Для обозначения тысяч использовался специальный знак, а числовое значение буквы выделялось титлом, который представлял собой надстрочный знак. Эти системы чисел были важными элементами культуры и математики, позволяя эффективно записывать и передавать числовую информацию.

Числа записываются слева направо, начиная с наибольшего значения и переходя к меньшему. Особый случай составляют числа от 11 до 19, где единицы указываются перед десятками. Этот принцип сохраняется и в современном языке при произнесении чисел различного порядка. Например, в числе «шестьдесят один» сначала называют десятки («шестьдесят»), а затем единицы («один»). В случае с числом «шестнадцать» порядок меняется: сначала произносятся единицы («шесть»), за которыми следует суффикс «надцать», обозначающий добавление к десяти. Таким образом, наблюдается интересная закономерность в структуре чисел, которая помогает лучше понять их последовательность и логику.

Основными преимуществами этих систем являлись их гармоничное сочетание с письменностью и доступность для образованных людей той эпохи. Это обеспечивало эффективное взаимодействие и способствовало распространению знаний среди интеллектуалов.

Позиционные системы счисления

Непозиционные системы счисления, несмотря на свою историческую важность, обладают значительными недостатками, что стало причиной их вытеснения позиционными системами в большинстве областей. Основные проблемы непозиционных систем заключаются в сложности выполнения арифметических операций, недостаточной эффективности в представлении больших чисел и отсутствия универсальности в использовании. Эти ограничения сделали позиционные системы более предпочтительными для научных, технических и повседневных расчетов. Позиционные системы, такие как десятичная и двоичная, обеспечивают простоту и удобство, что способствовало их широкому распространению и применению в различных сферах жизни.

• Сложность арифметических действий — например, в римской системе умножение и деление требуют сложных поэтапных вычислений.
• Отсутствие универсальности — каждая система требует уникального набора символов, что затрудняет международное взаимодействие.
• Громоздкость — большие числа требуют чрезмерно много символов.

Позиционные системы счисления обладают высокой удобностью. В таких системах исключаются разночтения при записи чисел, так как каждое число представляется однозначно благодаря использованию фиксированного количества разрядов. Более того, в позиционных системах нет ограничений на количество разрядов, что позволяет записывать числа любой величины. Это делает позиционные системы незаменимыми в математике и программировании, где точность и ясность записи чисел имеют первостепенное значение.

Позиционные системы подразделяются на две ключевые категории: однородные и неоднородные (смешанные). Важно рассмотреть уникальные характеристики каждой из этих систем. Однородные системы обладают постоянной базой, что упрощает вычисления и делает их более предсказуемыми. Неоднородные же системы могут включать в себя различную базу, что позволяет использовать большее количество символов и разнообразие в представлении чисел. Понимание этих характеристик поможет лучше ориентироваться в области числовых систем и их применения.

Однородная система счисления представляет собой позиционную систему, в которой одно основание используется для всех разрядов числа. Значение числа в этой системе определяется как цифрами, так и их расположением. Каждая позиция имеет определённый «вес», который соответствует основанию системы, возведённому в степень, соответствующую номеру позиции. Чтобы вычислить значение числа, необходимо умножить каждую цифру на вес её позиции и сложить полученные результаты. Однородные системы счисления являются основой для понимания более сложных математических концепций и широко применяются в различных областях, включая вычисления и компьютерные технологии.

Наиболее популярными позиционными системами счисления являются двоичная, восьмеричная, десятичная и шестнадцатеричная. Эти системы широко используются в информатике и математике для представления чисел. Двоичная система состоит из двух цифр, 0 и 1, и является основой компьютерных технологий. Восьмеричная система оперирует восемью цифрами, от 0 до 7, и применяется в некоторых областях программирования. Десятичная система, состоящая из десяти цифр, является наиболее привычной для человека и используется в повседневной жизни. Шестнадцатеричная система включает шестнадцать символов, от 0 до 9 и от A до F, и часто используется в программировании для упрощения представления двоичных данных. Каждая из этих систем имеет своё применение и важность в различных областях науки и техники.

Двоичная система чисел использует всего два символа: 0 и 1. В этой системе каждая позиция числа соответствует степени двойки, начиная с нулевой степени справа. Например, число 42 в двоичной системе представлено как 101010. В этом представлении каждая позиция соответствует определенной степени двойки: 32 (2^5) + 0 (2^4) + 8 (2^3) + 0 (2^2) + 2 (2^1) + 0 (2^0) = 42. Понимание двоичной системы важно для работы с компьютерами и цифровыми технологиями, так как вся информация в них обрабатывается именно в этом формате.

Данная система нашла широкое применение в области вычислительной техники. Она используется для оптимизации процессов обработки данных, повышения эффективности вычислений и улучшения производительности оборудования. Благодаря своей универсальности, система активно внедряется в различных сферах, включая информационные технологии, научные исследования и промышленность. Эффективность данной системы способствует ее популярности среди разработчиков и инженеров, что делает её ключевым элементом в современных вычислительных решениях.

• Простота реализации — электронные схемы эффективно работают с двумя состояниями: наличием либо отсутствием электрического тока.
• Надёжность — использование всего двух состояний значительно уменьшает вероятность ошибок при передаче и обработке сигналов.
• Экономичность — обработка двоичных данных требует минимума компонентов: транзисторов, резисторов, конденсаторов и микросхем.

Читайте также:

Двоичная система счисления, также известная как бинарная, представляет собой систему, основанную на двух цифрах: 0 и 1. Она является основой работы современных компьютеров и цифровых устройств. В отличие от десятичной системы, где используются десять цифр (от 0 до 9), двоичная система применяет только две.

Понимание двоичной системы важно для специалистов в области информационных технологий, программирования и компьютерных наук. Основные операции, такие как сложение, вычитание и умножение, в двоичной системе выполняются аналогично десятичной, но с учетом только двух возможных значений.

Для преобразования числа из десятичной системы в двоичную необходимо делить число на 2 и записывать остатки от деления. Полученные остатки читаются в обратном порядке. Например, чтобы перевести число 10 в двоичную систему, делим его на 2, получаем 5 с остатком 0. Далее делим 5 на 2, получаем 2 с остатком 1, затем 2 на 2, получаем 1 с остатком 0, и, наконец, 1 на 2, получаем 0 с остатком 1. Читая остатки с конца, получаем 1010 — это двоичное представление числа 10.

Двоичная система также используется в программировании, особенно в низкоуровневых языках, таких как Assembler. Знание двоичной системы позволяет разработчикам оптимизировать код и эффективно работать с памятью.

В заключение, двоичная система счисления является основополагающим понятием в IT-сфере и знание её основ необходимо для успешной работы в этой области.

Восьмеричная система чисел, основанная на восьми цифрах (от 0 до 7), представляет собой способ записи чисел, где каждое значение разряда определяется умножением на соответствующую степень числа 8. Например, число 147₈ в восьмеричной системе можно разложить следующим образом: 1 × 8² + 4 × 8¹ + 7 × 8⁰, что в итоге даёт 64 + 32 + 7, равное 103 в десятичной системе. Восьмеричная система часто используется в программировании и компьютерных науках, так как она упрощает представление двоичных данных.

Восьмеричная система счисления была разработана для упрощения работы с двоичными числами, обеспечивая более компактное представление данных. Это имело особое значение на ранних этапах развития компьютерных технологий, когда объем памяти был ограничен. Например, восьмеричное число 7₈ соответствует двоичному 111₂, а число 6₈ соответствует 110₂. Использование восьмеричной системы позволяет значительно сократить количество разрядов, необходимых для представления двоичных данных, что особенно важно в контексте программирования и работы с компьютерной памятью.

В современных компьютерных системах восьмеричная система счисления все еще используется, но на практике она часто уступает место шестнадцатеричной системе. Шестнадцатеричная система более эффективна для отображения байтов, так как один байт данных можно представить всего двумя шестнадцатеричными знаками. Это свойство делает шестнадцатеричную систему особенно удобной для низкоуровневого программирования и отладки программного обеспечения. Использование шестнадцатеричной системы упрощает восприятие и работу с данными, что особенно важно для разработчиков и системных администраторов.

Изучение актуальных тем и новостей имеет большое значение для расширения кругозора и получения свежей информации. Поддержание осведомленности о текущих событиях помогает не только в личном развитии, но и в профессиональной сфере. Обсуждение новых идей и технологий способствует обмену опытом и знаниями, что в свою очередь улучшает качество жизни и работы. Поэтому важно следить за тенденциями и анализировать их влияние на различные сферы деятельности. Не упустите возможность быть в курсе последних событий и открытий, чтобы оставаться конкурентоспособными и адаптивными в быстро меняющемся мире.

Бит и байт: руководство по единицам измерения информации

В мире цифровых технологий бит и байт являются основными единицами измерения информации. Бит (binary digit) представляет собой наименьшую единицу данных, которая может принимать одно из двух значений: 0 или 1. Это основа всех цифровых систем, от простейших до сложных.

Байт состоит из восьми бит и служит для хранения более сложной информации. Он может представлять различные символы, такие как буквы, цифры и знаки препинания. Благодаря этому байт стал стандартной единицей для измерения объема данных в компьютерной памяти и при передаче информации.

Важным аспектом является то, что в контексте хранения и передачи данных используются и более крупные единицы измерения, такие как килобайт, мегабайт, гигабайт и терабайт. Эти единицы облегчают понимание объема информации, который можно хранить или передавать.

Килобайт (КБ) равен 1024 байтам, мегабайт (МБ) — 1024 килобайтам, гигабайт (ГБ) — 1024 мегабайтам, а терабайт (ТБ) — 1024 гигабайтам. Понимание этих единиц поможет вам лучше ориентироваться в мире технологий, а также в вопросах, связанных с хранением и передачей данных.

Знание бит и байт является основой для понимания многих аспектов работы с информацией, включая программирование, администрирование систем и компьютерные сети. Это знание также важно для выбора подходящих устройств хранения и оценки их производительности.

Система записи чисел с использованием десяти цифр (от 0 до 9) основывается на том, что каждая позиция в числе представляет собой определённую степень числа десять. Например, число 567 можно представить в виде 5 × 10² + 6 × 10¹ + 7 × 10⁰, что эквивалентно упрощённому выражению 500 + 60 + 7. Это десятичная система счисления, которая широко используется в математике и повседневной жизни для представления чисел.

Десятичная система счисления возникла благодаря естественному фактору — десяти пальцам рук человека, которые с древних времен использовались для подсчета. Она получила широкое распространение в Индии в V–VI веках нашей эры. Через арабских математиков десятичная система пришла в Европу, заменив римские цифры. Это замещение существенно упростило выполнение сложных математических расчетов и стало основой для дальнейшего развития современной десятичной системы.

Десятичная система занимает важное место в нашей повседневной жизни и используется во многих сферах, включая торговлю, банковское дело, науку и технику. В денежных расчетах мы применяем рубли и копейки, где 1 рубль равен 100 копейкам. При измерении температуры часто используются градусы Цельсия с десятичными долями, например, 36,6 °C. Для точной записи дробных чисел в десятичной системе используются десятичная точка или запятая, что позволяет выражать числа с необходимой степенью точности. Это делает десятичную систему универсальным инструментом для количественных расчетов и анализа в различных областях.

Шестнадцатеричная система чисел использует 16 символов для записи данных. Она включает цифры от 0 до 9 и буквы A, B, C, D, E, F, которые представляют значения от 10 до 15. Эта система была разработана для эффективной работы с компьютерными данными, так как обеспечивает компактное представление двоичных чисел. Шестнадцатеричная система широко применяется в программировании и компьютерной технике, поскольку облегчает чтение и запись больших объемов данных.

Сегодня шестнадцатеричная система широко используется в различных сферах, включая программирование, веб-разработку и компьютерную графику. Она позволяет эффективно представлять данные и упрощает работу с большими числами. В программировании шестнадцатеричные значения часто применяются для обозначения цветов в веб-дизайне, а также в кодировании данных, что делает их незаменимыми для разработчиков. Кроме того, шестнадцатеричная система используется в системах машинного кода, что облегчает взаимодействие с низкоуровневыми языками программирования. Применение шестнадцатеричной системы способствует повышению производительности и улучшению читаемости кода.

• В веб-разработке — для обозначения цветов в CSS. Например, код #FF5733 обозначает оранжевый цвет.
• В криптографии — для представления хеш-значений. Так, код 8A4B2C1D служит для проверки целостности данных.
• В сетевых технологиях — для записи IP-адресов. Например, адрес 2001:0db8:85a3 используется в протоколе IPv6.
• В игровой индустрии — для отладки программ и тестирования игр, например, код 0xDEADBEEF указывает на сбой программного обеспечения.
• В системном программировании — для обозначения ошибок и состояний системы, где код 0×0000FFFF указывает на тип сбоя.

Читайте также:

Первый компьютер: как он выглядел и кто его создал

Первый компьютер, который можно считать предшественником современных вычислительных машин, появился в середине XX века. Этот исторический аппарат, известный как ENIAC (Electronic Numerical Integrator and Computer), был разработан в США. Создание ENIAC стало результатом работы ученых Джона Мокли и Преспера Эккерта в 1945 году.

ENIAC был огромным устройством, занимавшим целую комнату. Он использовал более 17 000 электронных ламп и потреблял огромное количество энергии. Основной задачей компьютера было выполнение сложных математических расчетов, что значительно ускоряло процесс по сравнению с ручным вычислением.

Другие ранние компьютеры, такие как UNIVAC и Z3, также внесли значительный вклад в развитие вычислительной техники. UNIVAC стал первым коммерческим компьютером, а Z3, созданный Конрадом Цузе, был одним из первых программируемых компьютеров.

Первые компьютеры имели ограниченные возможности и использовали перфокарты для ввода данных. Тем не менее, их создание стало основой для дальнейших инноваций в области информационных технологий. Современные компьютеры, обладающие высокой производительностью и многофункциональностью, развивались на основе тех первых идей и технологий.

Рассматривая историю первого компьютера, мы можем лучше понять, как далеко шагнула вычислительная техника и как она изменила нашу жизнь.

Смешанные системы счисления

Неоднородные, или смешанные, системы счисления представляют собой уникальный тип позиционных систем, в которых каждое основание может отличаться для разных разрядов. В таких системах численные значения записываются с использованием различных баз, зависящих от позиции каждой цифры. Главная особенность этих систем заключается в том, что вес каждой цифры определяется как произведение оснований всех младших разрядов. Это делает смешанные системы счисления интересными и сложными для анализа, так как они требуют учета различных оснований для точного вычисления значений.

Изучим смешанную систему счисления, в которой каждый разряд соответствует своему уникальному основанию: первый разряд использует основание 2, второй — основание 3, а третий — основание 4. Это представление записывается как [2, 3, 4]. В данной системе число 123 разбивается на составляющие, которые определяются в зависимости от оснований каждого разряда.

• Первая цифра (1) умножается на произведение всех младших оснований: 1 × (3 × 4) = 12.
• Вторая цифра (2) умножается на основание младшего разряда: 2 × 4 = 8.
• Третья цифра (3) умножается на 1: 3 × 1 = 3.
• Сумма всех значений (12 + 8 + 3) даёт число 23 в десятичной системе.

Вавилонская шестидесятеричная система чисел является одной из самых древних смешанных систем счисления. В этой системе используются символы, представляющие значения от 0 до 59, а каждый разряд соответствует степени числа 60. Значение каждого символа определяется его позицией в числе, при этом каждый следующий разряд увеличивает значение в 60 раз. Эта уникальная система была широко использована в древнем Вавилоне и оказала значительное влияние на развитие математики и астрономии.

Вавилонская система счисления основывалась на двух ключевых символах: вертикальном клине, обозначающем единицы, и горизонтальном клине, который указывал на десятки. Числа в этой системе записывались справа налево, и новый разряд начинался после определённой комбинации символов. Вертикальный клин выполнял двойную функцию, обозначая как единицу, так и число 60 с его степенями, что привело к возникновению термина «шестидесятеричная система». Позиционный характер этой системы проявлялся в том, что значение символа (1 или 60) зависело от его расположения в числе, что позволяло эффективно выражать более крупные значения. Вавилонская система оказала значительное влияние на развитие математических концепций и систем счисления, что делает её важным объектом изучения в истории математики.

С развитием торговли и астрономии вавилоняне начали записывать не только целые числа, но и дроби. Они усовершенствовали свою числовую систему, добавив дополнительные разряды после целой части. Таким образом, была создана смешанная форма записи: целая часть отображалась в шестидесятеричной системе, а каждый разряд дробной части представлял деление на 60. Это нововведение позволило более точно представлять и обрабатывать числовые значения, что было особенно важно в торговле и научных расчетах. В результате вавилонская система чисел оказала значительное влияние на развитие математики и астрономии в последующие эпохи.

Вавилонская система измерения времени оказала значительное влияние на создание современных измерительных приборов, включая наручные часы и высокоточные навигационные системы GPS. Рассмотрим, как это проявляется на примере современных часов с точным временем, например, 10:45:30. В данном формате каждый компонент времени использует свою уникальную систему счисления: часы могут отображаться в 12- или 24-часовом формате, тогда как минуты и секунды следуют 60-ричной системе, где значения варьируются от 0 до 59. Это разнообразие систем счисления демонстрирует, как древние методы измерения времени продолжают влиять на нашу жизнь и технологии сегодня.

Перевод из одной системы в другую

Разработчики часто сталкиваются с различными системами счисления. Существует множество ситуаций, в которых необходимо выполнять преобразования между ними. Например, при работе с базами данных и программированием важно конвертировать числа из десятичной системы в двоичную, восьмеричную или шестнадцатеричную. Также преобразования могут понадобиться при работе с различными протоколами передачи данных, где используются специфические форматы счисления. Понимание и умение выполнять такие преобразования является ключевым навыком для разработчиков, что позволяет им более эффективно решать задачи и оптимизировать свои проекты.

• При работе с битовыми операциями и масками для оптимизации кода и улучшения производительности программ. Например, число 1111 в двоичной системе (0b1111) соответствует F в шестнадцатеричной (0xF).
• При анализе и отладке программ для эффективного управления памятью и поиска ошибок. Пример: адрес в памяти 4095 в десятичной системе соответствует 0xFFF в шестнадцатеричной.
• При настройке сетевого оборудования для конфигурации и диагностики устройств. Например, IP-адрес 127.0.0.1 в десятичной записи соответствует 7F.00.00.01 в шестнадцатеричной.
• В криптографии и защите информации для обработки и верификации зашифрованных данных. К примеру, ключ шифрования может быть представлен как в двоичном, так и в шестнадцатеричном виде.
• При работе с цветовыми кодами в веб-разработке и графическом дизайне. Так, чистый синий цвет RGB (0, 0, 255) в десятичной системе записывается как #0000FF в шестнадцатеричной.

Существует три основных метода перевода чисел между системами счисления: деление с остатком, умножение с накоплением и применение таблиц соответствия. Каждый из этих методов имеет свои особенности и подходит для различных задач. Деление с остатком позволяет эффективно переводить числа из десятичной системы в другую, в то время как умножение с накоплением чаще используется для перевода в более сложные системы. Таблицы соответствия обеспечивают быстрый доступ к значениям и могут значительно упростить процесс перевода. Выбор метода зависит от конкретной задачи и предпочтений пользователя.

Метод деления с остатком используется для перевода чисел из одной системы счисления в другую. Процесс заключается в делении исходного числа на основание новой системы и записи остатка от деления. Эти действия повторяются с полученным частным до тех пор, пока оно не станет равным нулю. Остатки затем записываются в обратном порядке, что и дает искомый результат. Рассмотрим перевод числа 83₁₀ в двоичную систему счисления.

• 83 ÷ 2 = 41 (остаток 1);
• 41 ÷ 2 = 20 (остаток 1);
• 20 ÷ 2 = 10 (остаток 0);
• 10 ÷ 2 = 5 (остаток 0);
• 5 ÷ 2 = 2 (остаток 1);
• 2 ÷ 2 = 1 (остаток 0);
• 1 ÷ 2 = 0 (остаток 1);
• Результат: 83₁₀ = 1010011₂.

Метод умножения с накоплением представляет собой эффективный способ преобразования чисел из одной системы счисления в другую, например, из двоичной в десятичную. Этот метод включает два основных этапа. Сначала необходимо взять каждую цифру исходного числа и умножить её на основание системы, возведенное в степень, соответствующую позиции этой цифры (позиции считаются справа налево, начиная с нуля). После этого все полученные произведения складываются, чтобы получить итоговое значение в новой системе счисления. Рассмотрим пример перевода числа 101₂ в десятичную систему:

Метод умножения с накоплением представляет собой эффективный способ перевода чисел из одной системы счисления в другую, например, из двоичной в десятичную. Этот метод включает два основных этапа. Вначале каждая цифра исходного числа умножается на основание системы, возведенное в степень, соответствующую позиции цифры. Позиции считаются справа налево, начиная с нуля. После этого результаты умножения суммируются, что позволяет получить итоговое значение в целевой системе счисления. Данный метод является важным инструментом в математике и информатике, позволяя легко осуществлять конвертацию чисел между различными системами счисления.

Для перевода двоичного числа 101₂ в десятичную систему, необходимо учитывать значения каждого бита. В двоичной системе каждый бит представляет степень числа 2, начиная с 0 справа налево.

В данном случае, число 101₂ можно разбить на отдельные биты: 1, 0 и 1. Воспользуемся формулой для перевода:

1 * 2² + 0 * 2¹ + 1 * 2⁰.

Теперь вычислим каждое выражение:

1 * 2² = 4,
0 * 2¹ = 0,
1 * 2⁰ = 1.

Теперь сложим полученные значения:

4 + 0 + 1 = 5.

Таким образом, двоичное число 101₂ в десятичной системе будет равно 5.

• Первая цифра справа (1): 1 × 2⁰ = 1.
• Средняя цифра (0): 0 × 2¹ = 0.
• Последняя цифра (1): 1 × 2² = 4.
• Складываем: 4 + 0 + 1 = 5₁₀.

Таблицы соответствия представляют собой эффективный способ перевода чисел. Они основаны на заранее подготовленных таблицах, которые отображают соответствие между цифрами различных систем счисления. Использование таких таблиц значительно упрощает процесс конвертации чисел. В интернете можно найти множество ресурсов, предлагающих эти таблицы, что делает их доступными для всех.

• RapidTables — универсальный онлайн-конвертер для всех основных систем счисления.
• BaseCalc — сервис для перевода чисел между системами счисления с основаниями от 2 до 36.
• Online Binary-Decimal Converter — инструмент для быстрого перевода между двоичными и шестнадцатеричными числами.
• Calculator.net — калькулятор с поддержкой шестнадцатеричных, двоичных, десятичных и восьмеричных вычислений.
• Math Is Fun — полезный образовательный ресурс с подробными объяснениями процесса конвертации чисел.
• WolframAlpha — продвинутый математический ресурс, который не только конвертирует числа, но и показывает пошаговое решение.

Современные языки программирования предлагают мощные инструменты для конвертации между различными системами счисления. Использование встроенных функций этих языков значительно упрощает процесс преобразования данных, что экономит время и снижает вероятность ошибок. Это делает их отличным дополнением к уже описанным методам, позволяя разработчикам эффективно решать задачи, связанные с преобразованием чисел.

JavaScript предлагает множество методов, которые позволяют разработчикам эффективно управлять функциональностью веб-страниц. К числу популярных методов можно отнести обработку событий, манипуляцию с элементами DOM, а также взаимодействие с сервером через AJAX. Используя методы JavaScript, разработчики могут создавать динамичные и интерактивные пользовательские интерфейсы. К примеру, методы для работы с массивами, такие как `map`, `filter` и `reduce`, позволяют оптимизировать обработку данных, обеспечивая быструю и удобную работу с коллекциями. Кроме того, возможности JavaScript по асинхронному программированию с использованием `async/await` и `Promises` делают его мощным инструментом для создания отзывчивых веб-приложений. Эти методы позволяют не только улучшить производительность, но и повысить удобство в использовании создаваемых приложений.

Для получения информации о работе с системами счисления рекомендуется обратиться к официальной документации. Подробные руководства доступны для популярных языков программирования, таких как Python, JavaScript, Java, C++, Ruby, PHP и Go, что позволяет разработчикам эффективно использовать различные системы счисления в своих проектах.