Теория графов: основные понятия, виды, свойства и способы применения / Skillbox Media

Содержание:

• Что такое граф
• Основные понятия теории графов
• Путь, цепь и цикл в графе
• Виды графов
• Деревья в графах
• Что запомнить

Что такое граф

Граф представляет собой математическую структуру, предназначенную для моделирования связей между различными объектами. Он состоит из вершин и рёбер, которые соединяют эти вершины. Графы широко применяются в различных областях, таких как информатика, социальные науки и биология, для анализа и визуализации отношений и взаимодействий. Использование графов позволяет эффективно решать задачи, связанные с поиском путей, оптимизацией и кластеризацией данных.

Графы легче всего понять через конкретный пример. Рассмотрим три города с простыми названиями A, B и C, которые соединены дорогами: AB, AC и BC. Визуально это можно представить в виде графа, где города — это вершины, а дороги — рёбра, связывающие эти вершины. Такой подход позволяет наглядно увидеть, как графы функционируют и как они могут быть использованы для моделирования различных систем и отношений в реальном мире.

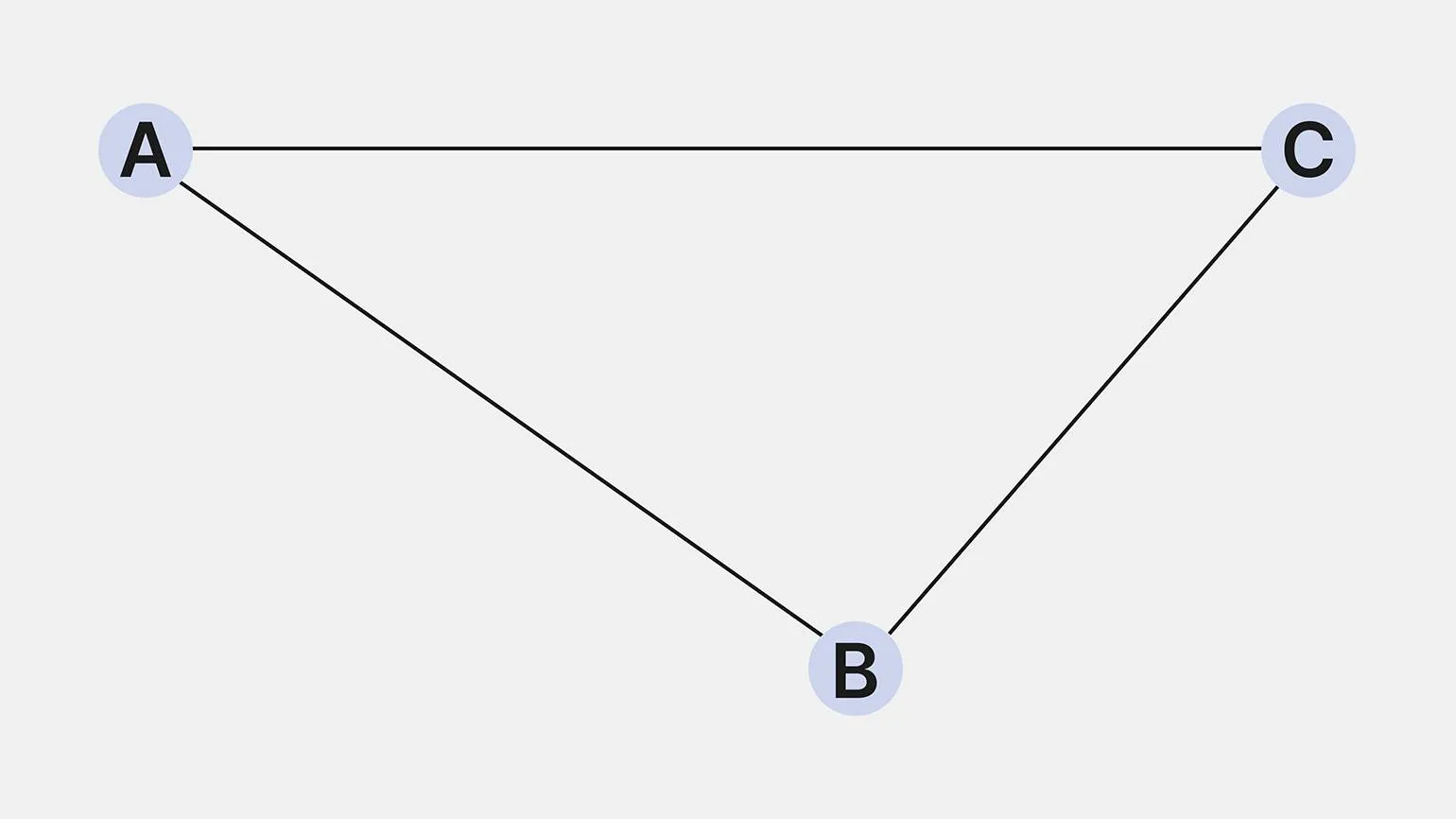
Получившийся рисунок представляет собой граф, который включает в себя несколько ключевых элементов. Граф состоит из узлов и рёбер, где узлы представляют собой объекты или вершины, а рёбра обозначают связи между ними. Эти элементы взаимодействуют друг с другом, образуя структуру, которая позволяет анализировать и визуализировать данные. Графы широко используются в различных областях, включая математику, информатику и социальные науки, для моделирования сложных систем и выявления закономерностей.

• Вершины. Ключевые точки или объекты в графе. Это могут быть, например, города на карте, веб-страницы в интернете или отделы в компании.
• Рёбра. Линии, которые соединяют вершины. Например, дорога между двумя городами, гиперссылка между веб-страницами или взаимодействие между отделами в компании.

Графы эффективно отображают сложные связи, которые не поддаются другим методам визуализации. Например, с помощью графа можно создать карту социальных связей, где вершины представляют людей, а рёбра иллюстрируют их взаимоотношения. Такой подход позволяет наглядно увидеть структуру и динамику социальных взаимодействий, что делает графы незаменимым инструментом в аналитике и исследовании социальных сетей.

Основные понятия теории графов

В графах рёбра и вершины могут устанавливаться различные виды связей, что обеспечивает гибкость в моделировании отношений между объектами. Это позволяет более точно и наглядно отображать полезную информацию на графических представлениях. Разнообразие связей в графах способствует лучшему пониманию структуры данных и их взаимосвязей.

Ребро, которое соединяет две вершины, называется инцидентным этим вершинам. Например, ребро AB связывает вершины A и B, и, следовательно, оно инцидентно как вершине A, так и вершине B. Инцидентность — это отношение, которое существует исключительно между вершиной и ребром; две вершины или два ребра не могут быть инцидентными друг другу. Понимание инцидентности важно для изучения графов и их структуры, так как это определяет взаимосвязи между элементами графа и помогает в анализе его свойств.

Рёбра в графах могут быть направленными и ненаправленными. Ненаправленное ребро существует между вершинами A и B, если из A можно добраться до B и обратно. Примером ненаправленного ребра является дорога между городами A и B, по которой возможно передвигаться как в одном, так и в другом направлении. Таким образом, ненаправленное ребро связывает вершины A и B, обеспечивая взаимосвязь между ними.

Если из точки A можно добраться до точки B, но обратный путь невозможен, то связь между ними будет направленной от A к B. Ненаправленные связи могут иллюстрировать не только транспортные маршруты между городами, но и отношения в социальных сетях. Например, если пользователь подписался на другого пользователя, но тот не подписался в ответ, такая связь считается ненаправленной.

Графы классифицируются по направлению рёбер. Если все рёбра имеют направление, то такой граф называется направленным или ориентированным. В случае, когда рёбра не имеют направления, граф называется ненаправленным или неориентированным. Если в графе присутствуют как направленные, так и ненаправленные рёбра, он классифицируется как смешанный граф. Понимание этих категорий графов важно для анализа структур и алгоритмов в различных областях, таких как информатика, математика и сети.

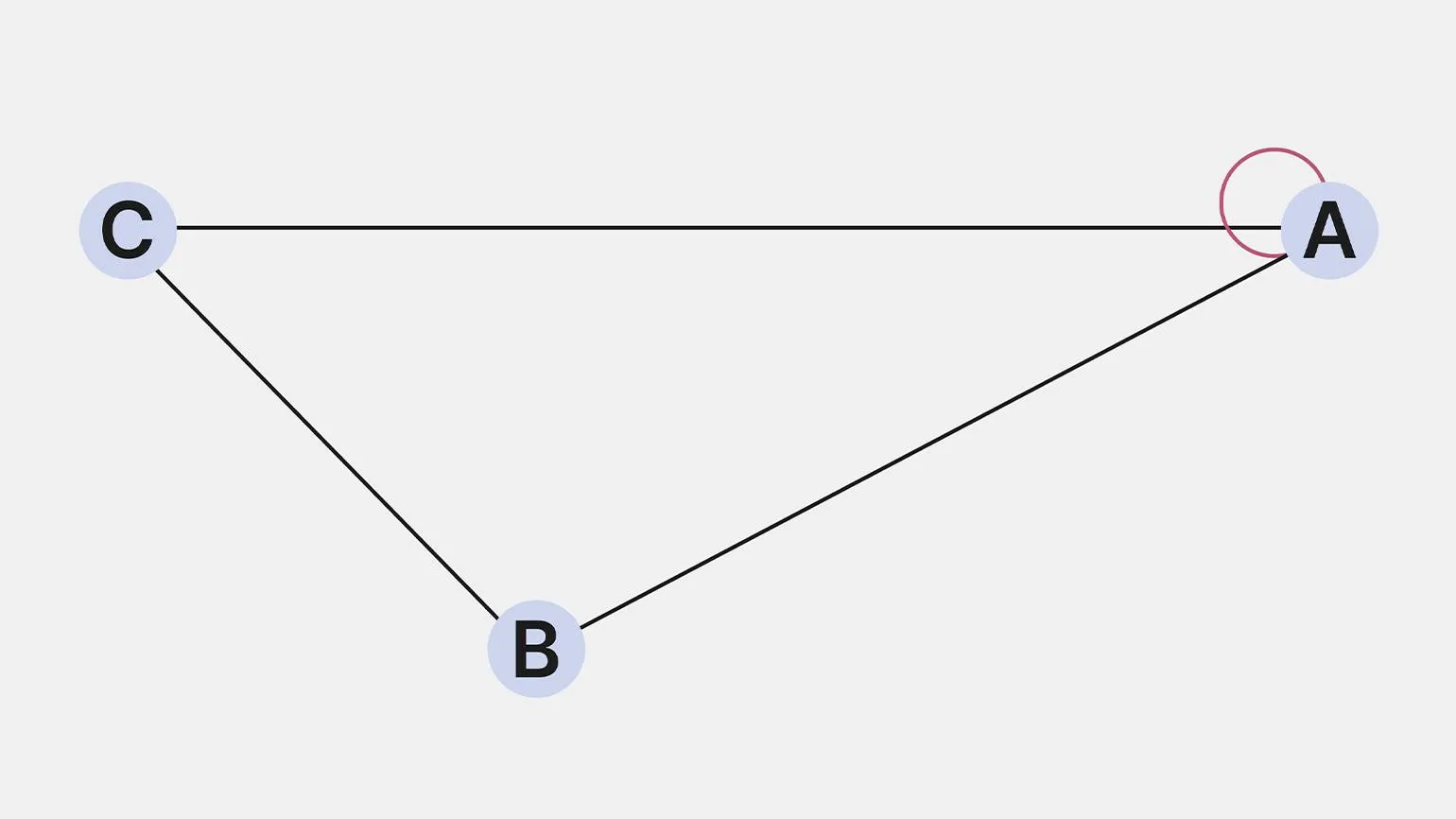
Петля, также известная как цикл, представляет собой уникальный тип ребра, который начинается и завершается в одной и той же вершине. В контексте социальных сетей петля может, например, обозначать ситуацию, когда пользователь отправляет сообщение самому себе. Если в графе отсутствуют петли, такой граф классифицируется как ациклический. Ациклические графы имеют важное значение в различных областях, включая компьютерные науки и теорию графов, так как они обеспечивают более простую структуру для анализа и обработки данных.

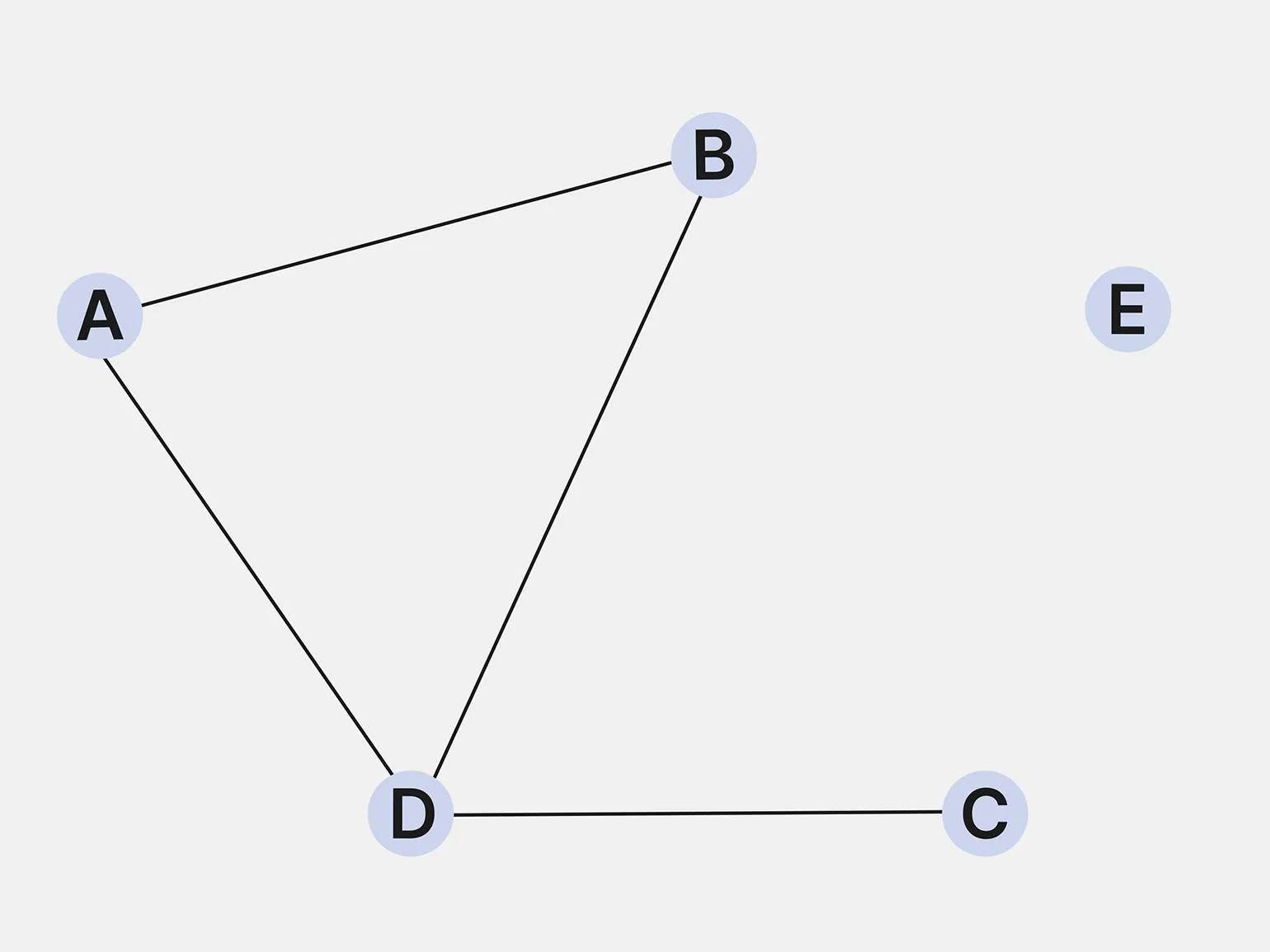
Вершины графа обладают уникальными свойствами, которые играют ключевую роль в теории графов. Каждая вершина может быть связана с другими вершинами через рёбра, что определяет структуру графа. Вершины могут иметь различные атрибуты, такие как степень, которая указывает количество рёбер, соединяющих данную вершину с другими. Также важно учитывать, что вершины могут быть классифицированы по типу — например, в ориентированных графах они могут быть исходными или конечными. Эти характеристики позволяют анализировать графы, выявлять их особенности и применять их в различных областях, таких как информатика, социальные сети и транспортные системы. Понимание свойств вершин графа является основой для более глубокого изучения их взаимодействий и применения в практических задачах.

• Если две вершины соединены ребром, то их называют смежными.
• Вершина без инцидентных рёбер — изолированная вершина.
• Если у вершины есть только одна связь с другими объектами в графе, то её называют висячей.
• Степень вершины — количество рёбер, которые выходят из неё.

Путь, цепь и цикл в графе

В теории графов понятия пути, цепи и цикла представляют собой основные способы перемещения между вершинами графа. Путь — это последовательность вершин, в которой каждая пара соседних вершин соединена ребром. Цепь, в свою очередь, может включать повторяющиеся вершины и ребра, что делает ее более гибкой в использовании. Цикл — это особый вид пути, который возвращается в исходную вершину, формируя замкнутую цепь. Эти концепции играют ключевую роль в решении задач, связанных с поиском оптимальных маршрутов и моделированием сложных систем взаимосвязей. Понимание этих основополагающих элементов теории графов позволяет эффективно анализировать и оптимизировать сети, что находит применение в различных областях, от логистики до компьютерных наук.

Разновидности маршрутов в графах включают несколько ключевых типов, каждый из которых имеет свои особенности и применения. Основные категории маршрутов в графах можно выделить как простые, циклические, кратчайшие и оптимальные.

Простые маршруты представляют собой последовательности ребер, которые не содержат повторяющихся вершин. Циклические маршруты, в свою очередь, начинаются и заканчиваются в одной точке, образуя замкнутый контур. Кратчайшие маршруты фокусируются на минимизации общей длины или веса, что делает их актуальными для задач оптимизации. Оптимальные маршруты могут учитывать различные критерии, такие как время, стоимость или другие параметры.

Понимание различных разновидностей маршрутов в графах имеет важное значение в таких областях, как логистика, транспорт, компьютерные науки и сетевые технологии. Это знание помогает эффективно планировать маршруты, обеспечивая снижение затрат и повышение производительности.

• Путь — конечная или бесконечная последовательность вершин и рёбер, в которой конец одного ребра является началом следующего.
• Цепь — это последовательность рёбер, в которой каждое ребро связано со следующим с помощью общей вершины. В цепи могут повторяться вершины, но не рёбра.
• Цикл — особый случай пути, который начинается и заканчивается в одной и той же вершине. При этом все рёбра и вершины (кроме начальной и конечной) уникальны. Важное условие цикла: вы не должны проходить по одному и тому же ребру дважды.

Виды графов

Существует множество типов графов, каждый из которых эффективно демонстрирует различные связи между объектами. Графы являются мощным инструментом для визуализации данных и анализа взаимосвязей, позволяя лучше понимать структуру и динамику систем. Разные виды графов, такие как направленные, ненаправленные, взвешенные и невзвешенные, применяются в различных областях, от социальных сетей до научных исследований, обеспечивая глубокое понимание межобъектных взаимодействий.

• Ориентированный. Граф, в котором каждое ребро указывает своё направление с помощью стрелок, по которым можно передвигаться. Например, когда есть путь A → B → C, но нет обратных рёбер; вернуться из C в A нельзя.
• Неориентированный. Граф, в котором рёбра не указывают направление. Это значит, что из любой вершины можно попасть в любую точку графа.
• Смешанный. Граф, который содержит как ориентированные, так и неориентированные рёбра.

• Граф с петлями. Рёбра графа, которые начинаются и заканчиваются в одной и той же вершине, называются петлями. Например, если мы строим схему связей в социальной сети, то с помощью петли можно показать, что пользователь ставит лайки своим же публикациям.
• Мультиграф. Если между двумя графами существует несколько рёбер, то такой граф будет называться мультиграфом. Такие графы часто используются в схемах транспортных систем, когда между городами есть несколько разных маршрутов (железная дорога, автомобильная дорога и авиарейсы).

Пустой граф представляет собой тип графа, не имеющего рёбер. Хотя такой граф может содержать вершины, между ними отсутствуют какие-либо соединения. Это позволяет визуализировать системы, в которых объекты не взаимодействуют друг с другом. Например, в контексте социальной сети пустой граф может обозначать человека, который не имеет никаких контактов или коммуникации с другими людьми. Такой подход позволяет наглядно демонстрировать изолированные элементы в различных моделях и системах.

Полный граф — это структура, в которой каждая вершина соединена ребром со всеми остальными вершинами. Такой граф идеально иллюстрирует коллектив, в котором каждый участник знаком с каждым другим. Полные графы являются важным элементом теории графов и находят применение в различных областях, включая социальные сети, коммуникации и сетевую топологию. Понимание полного графа может помочь в анализе взаимодействий в группах и в оптимизации процессов, связанных с обменом информацией.

Связный граф представляет собой структуру, в которой существует путь между каждой парой вершин. Это означает, что из любой вершины можно добраться до любой другой, следуя по рёбрам графа. В таком графе отсутствуют изолированные вершины или группы вершин, которые не имеют связи с остальными элементами структуры. Связные графы являются важным объектом изучения в теории графов и находят применение в различных областях, таких как компьютерные сети, социальные сети и транспортные системы.

Взвешенный граф представляет собой тип графа, в котором каждому ребру назначено числовое значение, называемое весом. Вес может отражать различные характеристики, такие как расстояние, время, стоимость, мощность и другие параметры, связанные с соединением вершин. Взвешенные графы широко используются в различных областях, включая теорию графов, оптимизацию маршрутов, сетевые технологии и многие другие сферы, где необходимо учитывать количественные аспекты взаимодействий между узлами.

Между двумя городами проложены две дороги: асфальтированное шоссе и грунтовая дорога. Очевидно, что поездка на автомобиле по асфальту будет более комфортной и экономичной. В связи с этим вес ребра, представляющего шоссе, будет меньше.

Двудольный граф — это тип графа, в котором все вершины можно разделить на две отдельные группы. Важно, что рёбра соединяют только вершины из разных групп, что означает отсутствие рёбер между вершинами внутри одной и той же группы. Двудольные графы находят широкое применение в различных областях, включая теорию графов, алгоритмы поиска и моделирование сетей.

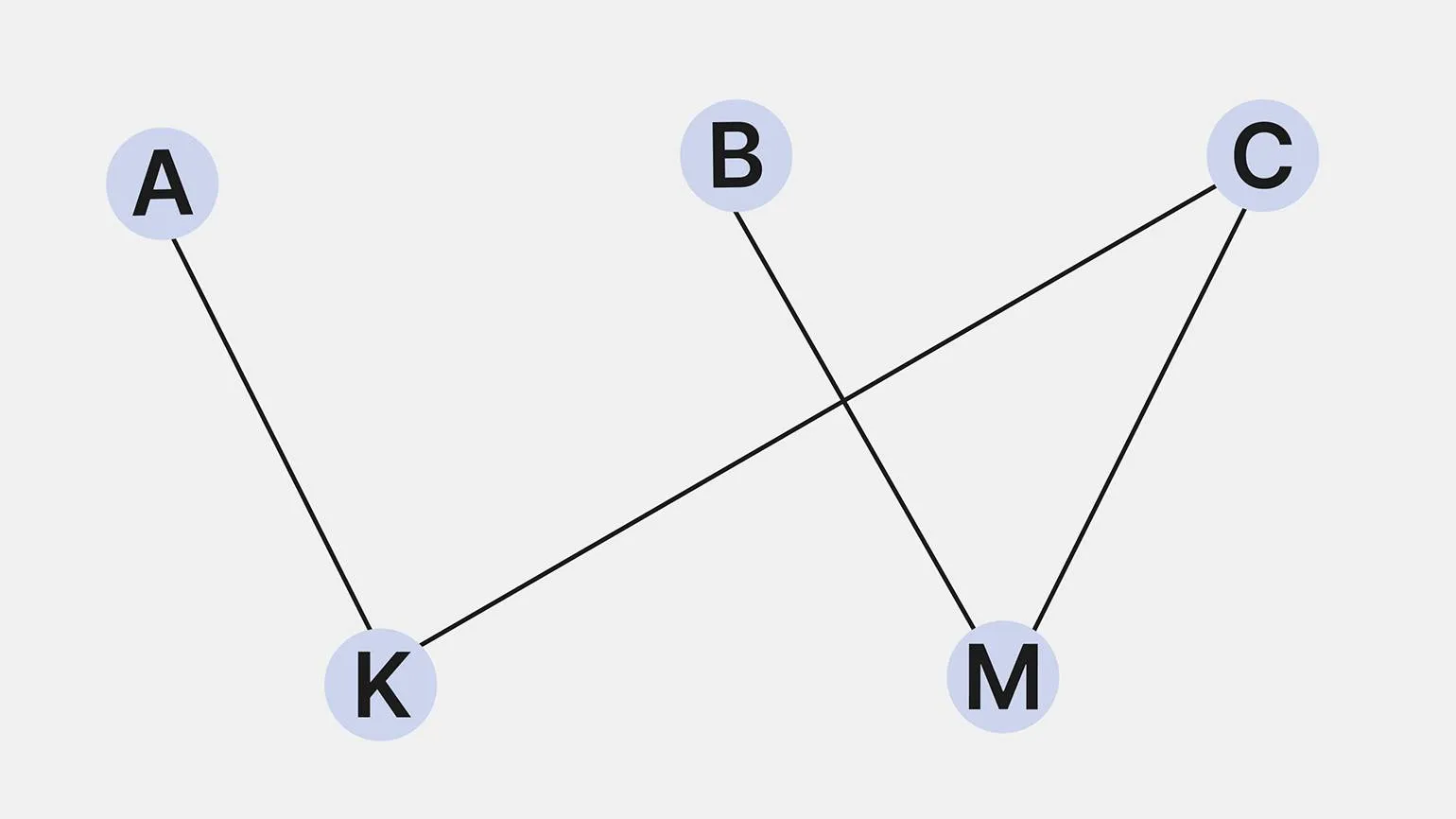
В данной ситуации мы можем рассмотреть взаимодействие между группой студентов и курсами, на которые они записываются, через графовую структуру. Граф будет включать в себя узлы, представляющие студентов и курсы, а также ребра, показывающие, какие студенты записаны на какие курсы. Это визуальное представление позволяет наглядно понять связи и взаимоотношения между участниками образовательного процесса. Графовая модель является эффективным инструментом для анализа учебных предпочтений и организации образовательного процесса, помогая выявить популярные курсы и распределение студентов по ним.

• Вершины из первой группы (A, B, C) — это студенты.
• Вершины из второй группы (K, M) — это курсы.
• Рёбра — запись студентов на курсы.

В приведенном примере студент A записан на курс K, студент B на курс M, а студент C одновременно на оба курса. Это создает ситуацию, в которой студенты, представляющие одно множество, соединены с курсами, принадлежащими другому множеству, но сами студенты не имеют соединений друг с другом. Таким образом, наблюдается четкая структура связей между студентами и курсами, что может быть проиллюстрировано в виде графа, где вершины студентов соединены с вершинами курсов, но внутренние связи между студентами отсутствуют.

Планарный граф представляет собой граф, который можно изобразить на плоскости, при этом его рёбра пересекаются исключительно в вершинах, а не в других местах. В теории графов планарные графы имеют особое значение, так как они позволяют изучать свойства графов в двумерном пространстве. Исследование планарных графов важно для различных приложений, включая компьютерную графику, проектирование сетей и оптимизацию маршрутов. Понимание планарных графов также связано с такими концепциями, как теорема Курамоты и алгоритмы для проверки планарности графов.

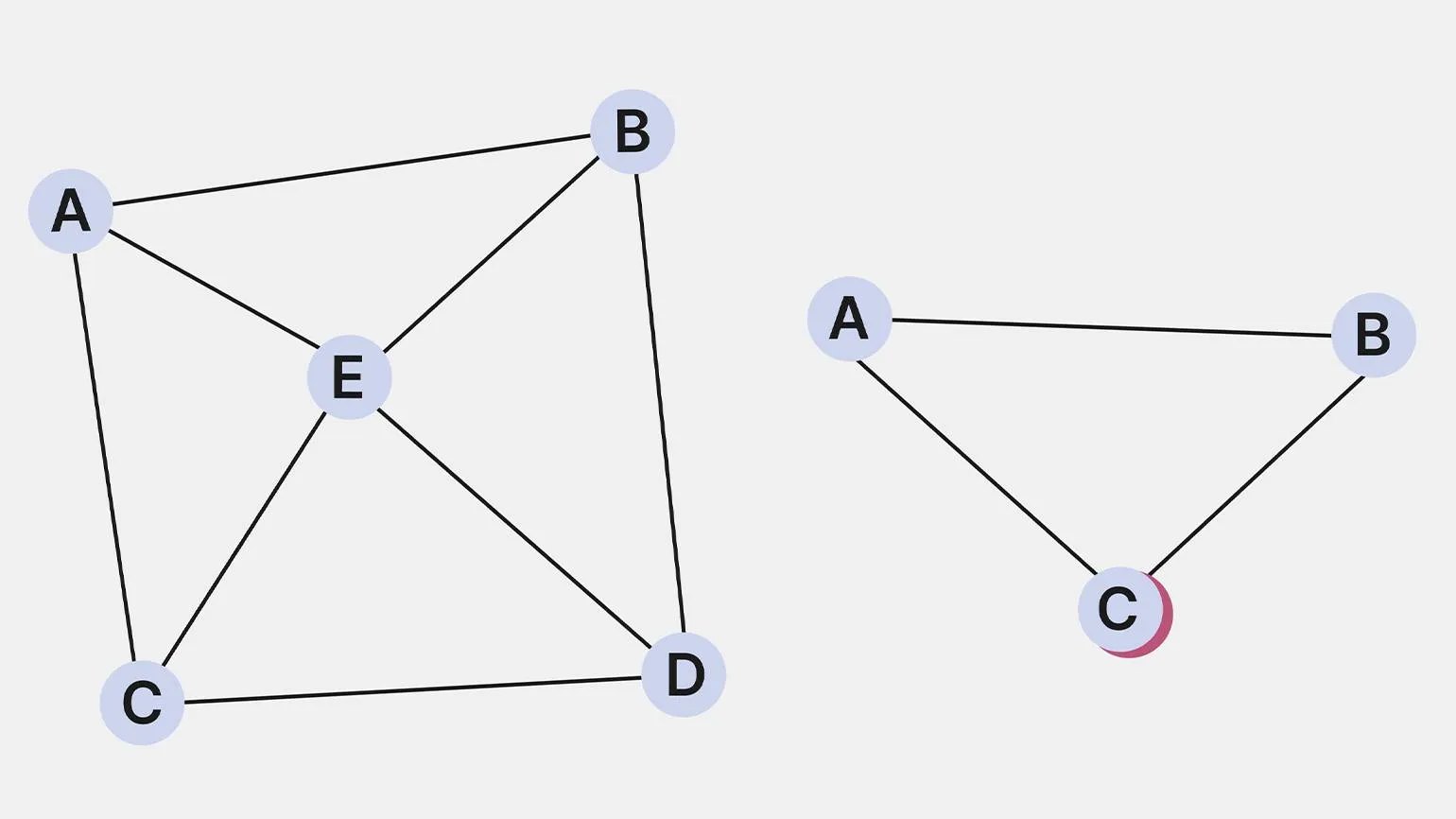
Эйлеров граф представляет собой граф, в котором имеется цикл, проходящий через каждое ребро ровно один раз и возвращающийся в начальную вершину. В дополнение к этому, существует понятие полуэйлерова графа, который также проходит по всем рёбрам ровно один раз, однако не возвращается в исходную вершину. Эйлеровы графы и полуэйлеровы графы играют важную роль в теории графов и имеют множество приложений в различных областях, включая математику, компьютерные науки и логистику. Понимание этих графов помогает в решении задач, связанных с маршрутизацией и оптимизацией.

Эйлеровы графы играют ключевую роль в решении задач оптимизации маршрутов. Их применение особенно эффективно при разработке туристических маршрутов и планировании логистических цепочек. Использование Эйлеровых графов позволяет находить оптимальные пути, минимизируя затраты времени и ресурсов. Это делает их незаменимыми инструментами в сфере туризма и логистики, где важно учитывать множество переменных для достижения максимальной эффективности.

Старинная математическая задача о кёнигсбергских мостах стала известным примером в истории математической теории. В городе Кёнигсберг, современном Калининграде, через реку Прегель, ныне называемую Преголя, было построено семь мостов. Вопрос заключался в том, возможно ли пройти по всем мостам, не пересекаясь с каждым из них более одного раза. В 1736 году этот вопрос решил великий математик Леонард Эйлер, который впервые применил теорию графов для анализа данной задачи. В процессе решения он создал концепцию циклических графов, которые впоследствии стали известны как эйлеровы графы в его честь. Эта задача не только стала основой для развития теории графов, но и продемонстрировала важность математического анализа в решении практических вопросов.

Прогулка по мостам в Калининграде невозможна. Если у вас есть сомнения, приезжайте и убедитесь в этом на собственном опыте.

Деревья в графах

Деревья — это особый тип графов, в которых отсутствуют циклы, но для каждой пары вершин существует уникальный путь. Эти структуры данных имеют важное значение в алгоритмах поиска и сортировки, обеспечивая эффективное представление и обработку информации. Благодаря своей иерархической структуре деревья позволяют оптимизировать доступ к данным, что делает их незаменимыми в различных областях, таких как компьютерные науки, базы данных и сетевые технологии.

Деревья обладают рядом ключевых свойств, которые делают их важными элементами экосистемы. Во-первых, они обеспечивают кислород, благодаря процессу фотосинтеза, что способствует улучшению качества воздуха. Во-вторых, деревья играют важную роль в сохранении водного баланса, предотвращая эрозию почвы и задерживая дождевую воду.

Кроме того, деревья служат естественным укрытием для множества видов животных и растений, поддерживая биологическое разнообразие. Их корневая система укрепляет грунт, снижая риск оползней и разрушений. Также деревья регулируют микроклимат, создавая тень и снижая температуру окружающей среды.

Важно отметить, что деревья являются долгосрочными углеродными поглотителями, что способствует борьбе с изменением климата. Их древесина используется в строительстве и производстве, что подчеркивает экономическую значимость деревьев. В целом, деревья играют незаменимую роль в нашем мире, обеспечивая как экологические, так и экономические преимущества.

• Между любыми двумя вершинами существует связь.
• Между любыми двумя вершинами есть единственный путь. Это означает, что не может быть двух разных путей, соединяющих одну и ту же пару вершин.
• В дереве с n вершин ровно n − 1 рёбер. Это фундаментальное свойство деревьев.

Существует множество видов деревьев, каждое из которых предназначено для выполнения определенных задач. Разнообразие деревьев позволяет использовать их в различных сферах, таких как ландшафтный дизайн, строительство, экология и садоводство. Каждое дерево имеет свои уникальные характеристики, которые делают его подходящим для конкретных условий и целей. Например, некоторые виды деревьев идеально подходят для создания тени или защиты от ветра, тогда как другие могут быть использованы для улучшения качества почвы или привлечения диких животных. Выбор правильного вида дерева зависит от климатических условий, типа почвы и желаемого результата. Правильный выбор и уход за деревьями могут существенно повысить их эффективность и долговечность, что делает их неотъемлемой частью природного и искусственного ландшафта.

• Корневое дерево. Это дерево, в котором одна вершина выделена как корень. В таком дереве определено направление вниз от корня к «листьям» (вершинам, не имеющим потомков). Вершины графа делятся на родительские и дочерние. Например, если вершина A родительская для B и C, то B и C — дочерние для A.

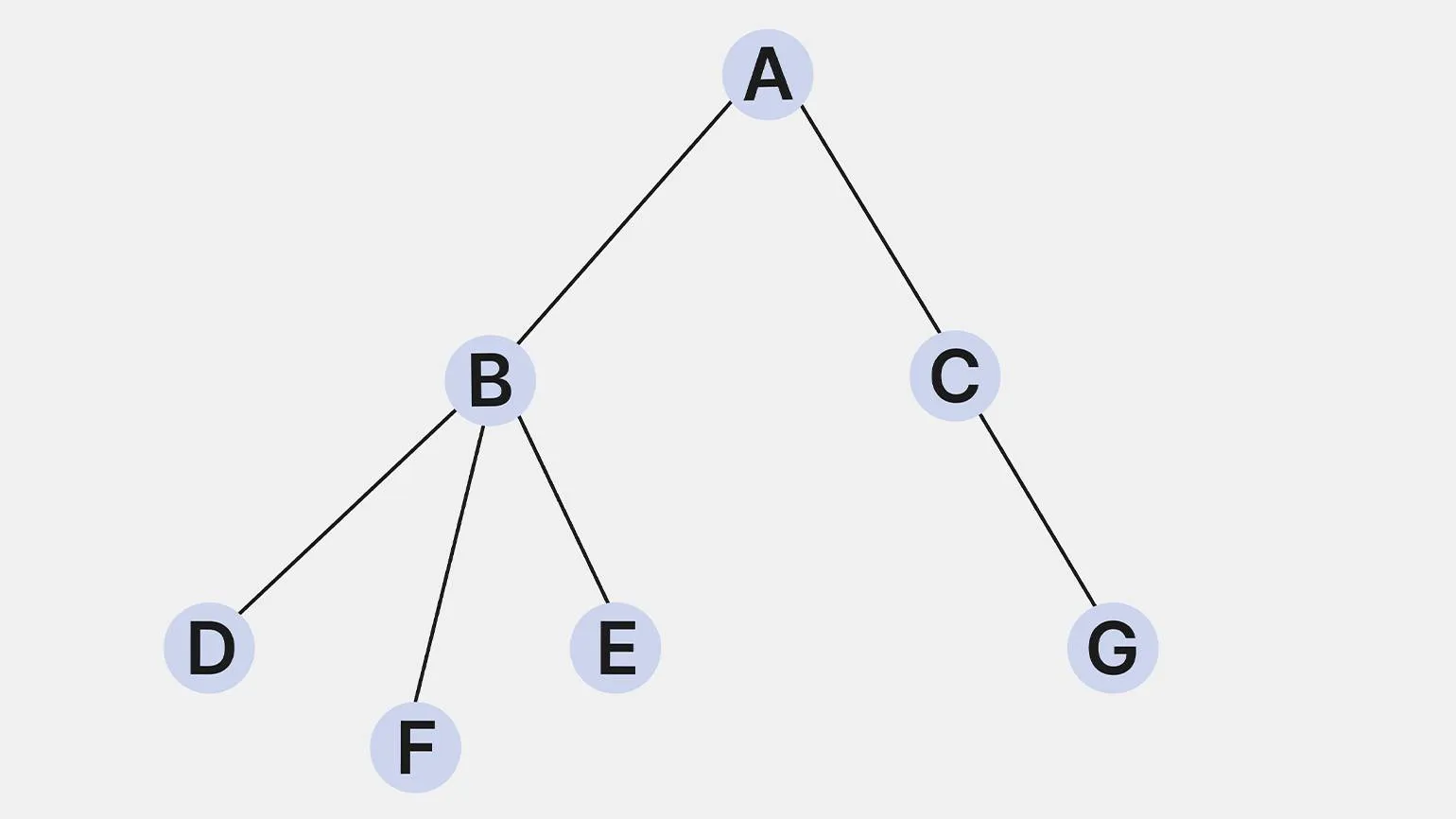
Структура файлов на компьютере представлена в виде иерархического дерева, где существует корневая директория, а также поддиректории и файлы, которые являются ее дочерними элементами. Эта организация позволяет пользователям эффективно управлять данными, обеспечивая удобный доступ к файлам и упрощая навигацию по системе. Корневая директория служит начальной точкой, от которой отталкиваются все остальные элементы файловой системы, что делает структуру логичной и понятной.

• Бинарное дерево. Это дерево, в котором каждая вершина имеет не более двух потомков. Бинарные деревья часто используются для организации поиска информации.

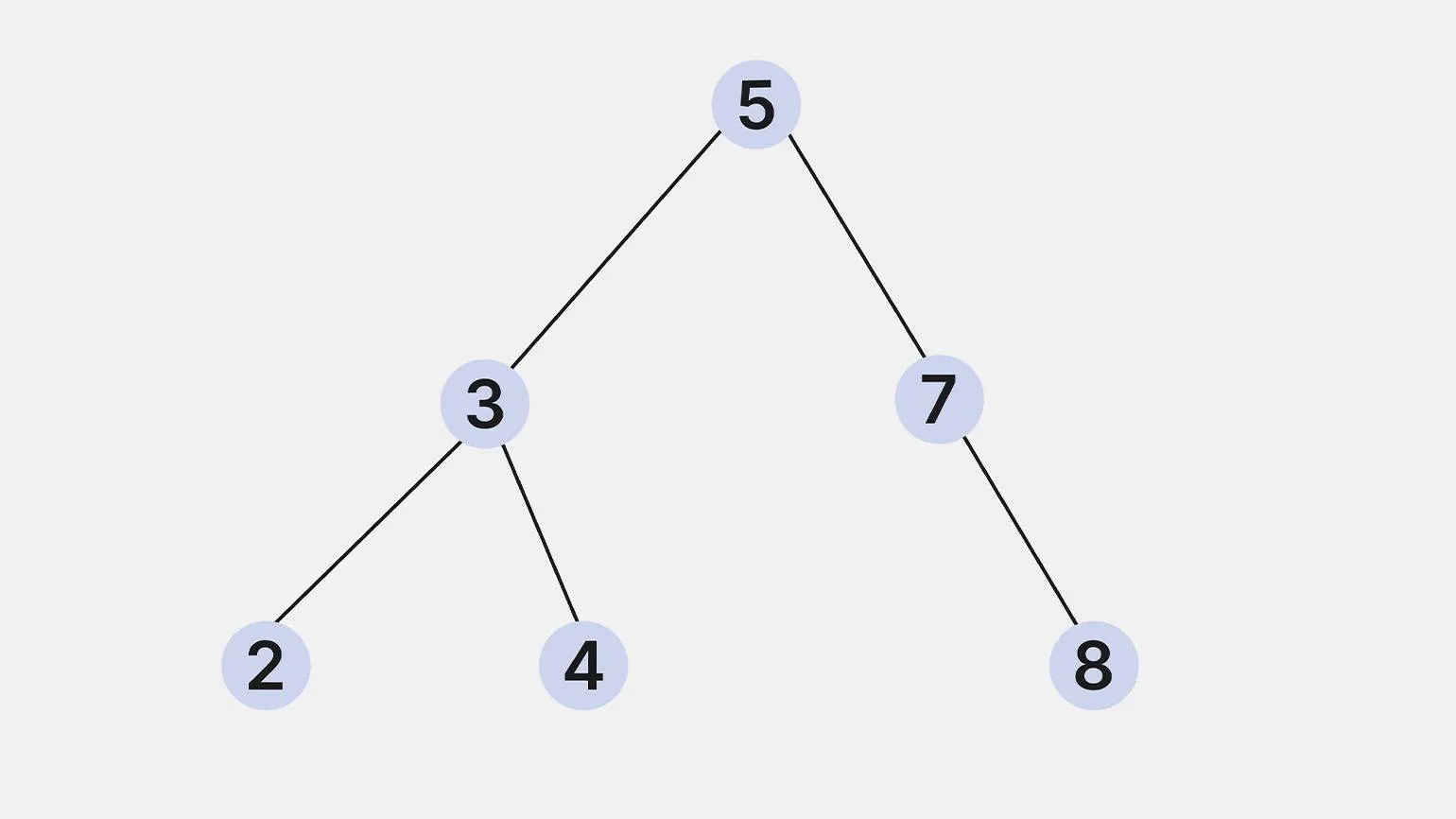
• Бинарное дерево поиска (BST). Бинарное дерево, в котором для каждого узла выполняется условие: значения всех узлов в левом поддереве меньше значения родительского узла, а в правом поддереве — больше или равны ему. BST обеспечивает эффективный поиск, вставку и удаление элементов.

Что запомнить

• Граф — это математическая структура, с помощью которой можно отображать различные объекты и взаимоотношения между ними. Графы состоят из вершин и связывающих их рёбер.
• У некоторых графов, например эйлеровых или деревьев, есть уникальные свойства, подходящие для решения специфичных задач.
• С помощью графов можно искать оптимальные маршруты, составлять карты социальных связей, строить схемы оборудования в локальной сети и организовывать поиск информации.