Машина Тьюринга: что это такое и как она работает / Skillbox Media

Содержание:

• Зачем она нужна
• Что такое машина Тьюринга и как она устроена
• Принцип работы машины Тьюринга
• Роль в истории
• Полнота по Тьюрингу
• Примеры реализации
• При чём тут грибы?

Термин «машина Тьюринга» знаком каждому, кто интересуется информатикой, компьютерами и информационными технологиями. Однако полное понимание этого концепта просто невозможно без глубокого изучения темы. Статья в «Википедии» не всегда дает исчерпывающие ответы, поэтому мы решили объяснить, что такое машина Тьюринга и почему она важна для информатики.

Машина Тьюринга — это абстрактная вычислительная модель, предложенная математиком Аланом Тьюрингом в 1936 году. Она служит основой для теории вычислений и помогает понять, что такое алгоритмы и какие задачи можно решить с помощью вычислительных систем. Машина состоит из бесконечной ленты, на которой записаны символы, и головки, способной читать и записывать эти символы, а также перемещаться по ленте.

С помощью машины Тьюринга можно формализовать понятия вычислимости и алгоритмической сложности, что является ключевым для разработки современных компьютерных программ и систем. Понимание работы этой модели позволяет лучше осознать границы возможного в вычислениях и важность алгоритмов в программировании.

Таким образом, изучение машины Тьюринга — это важный шаг на пути к глубокому пониманию информатики и IT.

Машина Тьюринга: ключевые аспекты и значение

Машина Тьюринга — это абстрактная модель вычислений, предложенная британским mathematician Аланом Тьюрингом в 1936 году. Она служит основой для теории вычислимости и играет важную роль в информатике и математике. Основная идея машины Тьюринга заключается в использовании бесконечной ленты, разделенной на ячейки, которые могут содержать символы, и механизма чтения и записи, управляемого набором правил.

Модель машины Тьюринга включает в себя следующие элементы: лента, головка чтения-записи, состояние машины и набор правил перехода. Лента представляет собой неограниченное хранилище данных, а головка перемещается по ленте, считывая и записывая символы. Состояние машины определяет текущую конфигурацию, а правила перехода описывают, как машина должна реагировать на прочитанные символы.

Машина Тьюринга является важным инструментом для понимания границ вычислений. Она позволяет определить, какие задачи могут быть решены алгоритмическим способом, а какие остаются нерешаемыми. Это делает её не только теоретическим, но и практическим инструментом в области разработки компьютеров и программного обеспечения.

Существуют различные варианты машин Тьюринга, включая недетерминированные и двунаправленные модели. Они помогают исследовать более сложные вычислительные процессы и оптимизировать алгоритмы. Понимание машины Тьюринга также способствует разработке новых языков программирования и улучшению архитектуры компьютерных систем.

В заключение, машина Тьюринга является фундаментальной концепцией в теории вычислений, которая продолжает оказывать влияние на развитие технологий и научные исследования.

• Зачем она нужна
• Как устроена
• Принцип работы
• Роль в истории
• Полнота по Тьюрингу
• Примеры реализации
• При чём тут грибы?

Зачем она нужна

В XVII веке выдающийся математик Готфрид Лейбниц высказывал амбициозную идею о разработке машины, способной определять истинность математических утверждений. Эта концепция стала основой для дальнейших исследований в области логики и вычислительной техники. Лейбниц стремился создать универсальный инструмент, который бы автоматически решал математические задачи и анализировал научные теории, предвосхищая идеи, которые позже легли в основу современного программирования и искусственного интеллекта. Его видение о машинном анализе знаний остаётся актуальным и в наши дни, стимулируя развитие новых технологий в вычислительной математике и автоматизированной логике.

Три века спустя выдающийся математик Давид Гильберт поставил задачу, стремясь найти алгоритм, способный принимать описание любой разрешимой проблемы в качестве входных данных. Этот алгоритм должен был по завершении конечного числа шагов предоставлять один из двух ответов: «истина» или «ложь».

В 1930-е годы к вопросу математики обратился известный ученый Макс Ньюман. Преподавая в Кембридже, он также занимался криптоанализом и сыграл ключевую роль в создании Colossus, который стал крупнейшим компьютером своего времени. Его работы оказали значительное влияние на развитие вычислительной техники и криптографии.

Существует ли универсальный метод или механический процесс, который можно использовать для проверки математических утверждений на их доказуемость? Вопрос о существовании такого метода остается актуальным в математике и философии науки. Исследования в этой области поднимают важные вопросы о границах формальной логики и алгоритмической проверки. Математики и логики продолжают изучать, возможно ли создать алгоритм, который сможет универсально определять, является ли данное математическое утверждение доказуемым.

Макс Ньютон в своих лекциях подчеркивает важность идей Алана Тьюринга, которые были подробно рассмотрены в книге Чарльза Петцольда «Читаем Тьюринга». Тьюринг внес значительный вклад в развитие вычислительной техники и теории вычислений, его работы остаются актуальными и сегодня. Книга Петцольда предлагает глубокий анализ тьюринговских концепций, что позволяет читателям лучше понять не только исторический контекст, но и современные приложения этих идей. Изучение трудов Тьюринга и их интерпретация Петцольдом помогает углубить знания о принципах работы алгоритмов и основах информатики.

Среди студентов университета Ньюмана находился ещё никому не известный математик Алан Тьюринг. Проведя время на лугах Гранчестера, популярном среди хипстеров того времени, он обдумывал идеи Ньюмана. Эти размышления привели к написанию статьи «On Computable Numbers, with an Application to the Entscheidungsproblem», в которой Тьюринг заложил основы для дальнейшего развития теории вычислимости и искусственного интеллекта.

Тьюринг, вероятно, с самого начала своей деятельности стремился продемонстрировать неразрешимость проблемы принятия решений (Entscheidungsproblem). Он поделился со мной, что «главная идея» его статьи пришла к нему во время отдыха на лугах Гранчестера летом 1935 года. Эта идея могла заключаться либо в его анализе вычислений, либо в понимании существования универсальной машины, что, в свою очередь, привело к диагональному аргументу для доказательства неразрешимости.

В воспоминаниях о Тьюринге, изложенных его учеником и другом Робином Ганди, содержится много интересных деталей о жизни и работе этого выдающегося ученого. В книге «The Universal Turing Machine. A Half-Century Survey» Рольфа Херкена освещаются основные достижения Тьюринга, его вклад в развитие вычислительной техники и теории алгоритмов. Эти воспоминания подчеркивают уникальность его мышления, а также влияние, которое он оказал на последующее поколение ученых. Тьюринг остается ключевой фигурой в истории информатики, и его идеи продолжают вдохновлять современных исследователей.

В данной статье, опубликованной в 1936 году, впервые была представлена концепция машины Тьюринга. Автор статьи использовал термин «вычислительная машина» (computing machine), который стал основой для дальнейшего названия модели. Эта работа сыграла ключевую роль в развитии теории вычислений и формировании основ современного компьютерного программирования.

Алан Тьюринг выбрал нетрадиционный подход, начиная с описания машины, выполняющей ряд простых операций. В то время компьютеры, как мы их знаем сегодня, еще не существовали, за исключением ранних вычислительных устройств, разработанных Чарльзом Бэббиджем и Вэниваром Бушем. Тьюринг сосредоточился на концептуальных основах вычислений, что стало основой для дальнейших исследований в области теории вычислений и информатики. Его работа положила начало формальному пониманию алгоритмов и вычислительных процессов, что стало важным этапом в истории компьютерной науки.

Что такое машина Тьюринга и как она устроена

Машина Тьюринга представляет собой абстрактную вычислительную модель, которая используется в теории вычислений и математической логике. Этот мысленный эксперимент был предложен Алланом Тьюрингом для решения основных вопросов о вычислимости. Основными компонентами машины Тьюринга являются бесконечная лента, считывающее- записывающее устройство и набор правил, определяющих действия машины. Лента служит местом для хранения данных и может быть использована для записи информации, считывающее- записывающее устройство перемещается по ленте, считывая и записывая символы в соответствии с заданными правилами. Благодаря своей универсальности, машина Тьюринга стала основой для разработки современных компьютеров и языков программирования, а также важным инструментом для понимания пределов вычислений.

• бесконечной ленты с ячейками;
• автомата или головки для чтения и записи;
• программы.

Машина оснащена «лентой» (аналогом бумаги), которая проходит через её механизм и разделена на участки, известные как квадраты. Каждый квадрат может содержать определённый символ.

Алан Тьюринг в своей работе «О вычислительных числах, с приложением к проблеме принятия решений» рассматривает фундаментальные аспекты вычислений и алгоритмов. Он вводит концепцию вычислимых чисел и формулирует задачу о принятии решений, что стало основой для дальнейших исследований в области теории вычислений. Тьюринг анализирует, как машины могут выполнять вычисления и решать математические проблемы, что открывает новые горизонты для развития информатики и искусственного интеллекта. Его идеи о Тьюринговых машинах и вычислимости продолжают оставаться актуальными и влиятельными в современных исследованиях. Работа Тьюринга стала ключевым вкладом в понимание границ вычислений и заложила основы для дальнейшего изучения теории алгоритмов и сложности.

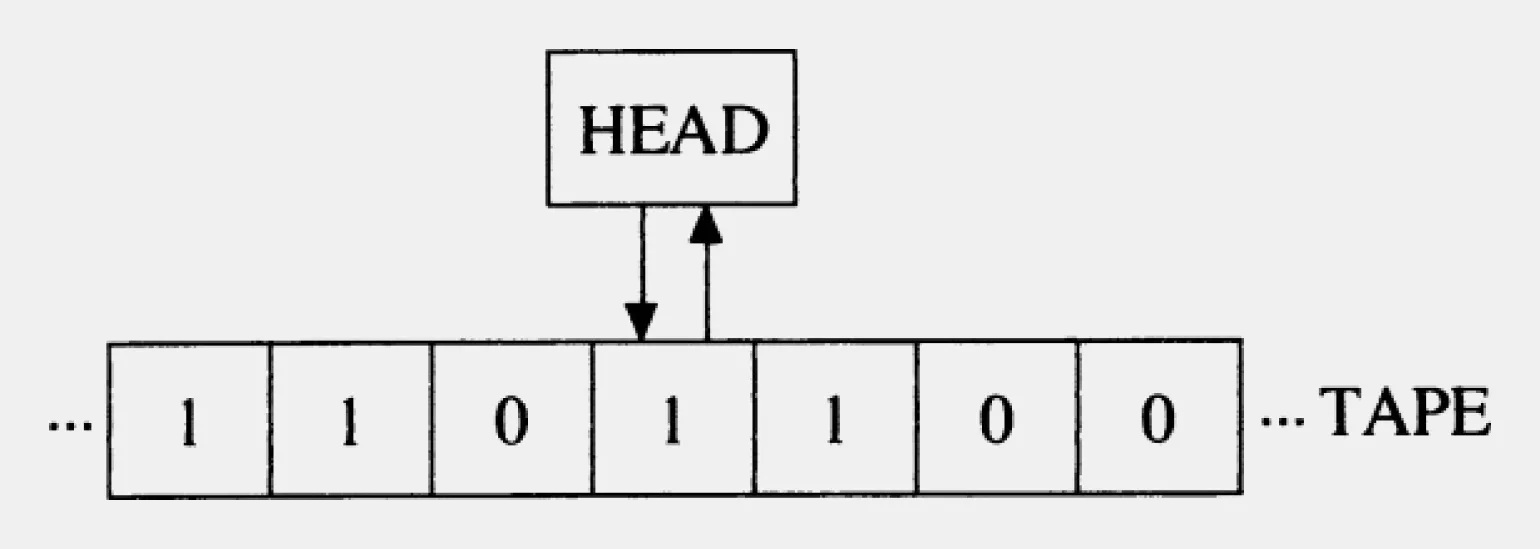
Принцип работы машины Тьюринга

Машина функционирует таким образом: головка способна считывать данные из определенной ячейки памяти, а также стирать, перезаписывать информацию и перемещаться влево или вправо к соседним ячейкам. После перемещения она вновь выполняет операции считывания или записи.

В определенных конфигурациях, когда ячейка пуста и не содержит символов, машина записывает новый символ в эту ячейку. В других случаях она может стереть существующий символ. Кроме того, машина способна изменять ячейку, смещая её содержимое на одно место вправо или влево. Эти операции являются основными действиями, которые выполняет машина в процессе обработки данных.

Алан Тьюринг в своей работе «О вычислительных числах, с приложением к проблеме принятия решений» рассматривает основы вычислительной теории и её связь с алгоритмами. Тьюринг вводит понятие вычислимых чисел и обсуждает, как они могут быть использованы для решения сложных математических задач. Важным аспектом его исследования является формулировка проблемы принятия решений, которая стала краеугольным камнем для дальнейших исследований в области информатики и теории вычислений. Работа Тьюринга оказала значительное влияние на развитие компьютерных наук и заложила основы для понимания границ вычислимости.

Действия головки управляются программой, представленная в виде таблицы, включающей внешний и внутренний алфавиты, а также таблицу переходов между ними. Внешний алфавит представляет собой конечное множество, элементы которого называются буквами или символами. Внутренний алфавит состоит из конечного множества состояний головки. Таблица переходов описывает поведение головки, определяя, как она должна реагировать на определенные символы. Конкретная команда для выполнения головкой определяется пересечением внешнего и внутреннего алфавитов в данной таблице. Это взаимодействие обеспечивает эффективное управление процессами и позволяет головке выполнять заданные операции в соответствии с программой.

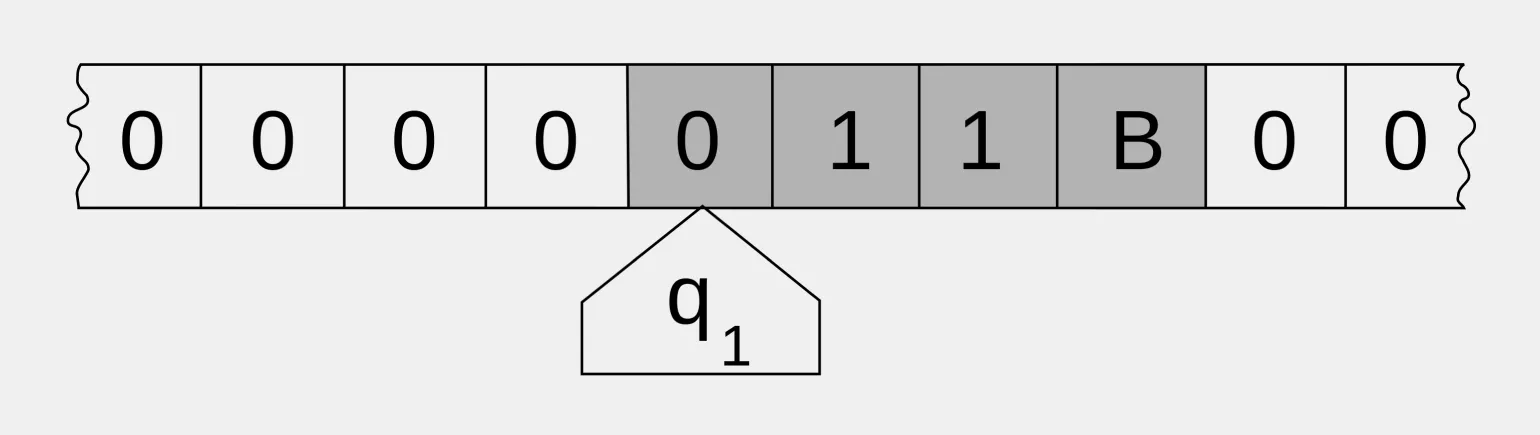
На представленном изображении показана лента, на которой входная информация (11В) размещена таким образом, что в каждой ячейке содержится по одному символу. С обеих сторон этой информации находятся нулевые ячейки. Начальное состояние головки обозначается как q1, что инициирует работу машины. Головка имеет возможность перемещаться влево, записывая вместо нуля цифру или букву, или смещаться вправо и перезаписывать единицу другой цифрой или буквой. Также она может перемещаться на одну ячейку влево или вправо без выполнения операции перезаписи.

Головка может оставаться на месте и не выполнять никаких действий. Операции прекращаются, когда головка считывает пассивное состояние — q0. Это состояние указывает на завершение процесса и отсутствие необходимости в дальнейших манипуляциях.

В чем заключается значимость этой, на первый взгляд, простой конструкции? Эта конструкция играет ключевую роль в различных процессах и системах, обеспечивая необходимую функциональность и эффективность. Понимание ее важности может значительно повлиять на результаты, которые мы хотим достичь. Она служит основой для более сложных решений и упрощает взаимодействие различных элементов. В итоге, даже самая простая конструкция может оказаться критически важной для достижения целей.

Роль в истории

Машина Тьюринга имеет историческое значение как первая математическая модель универсальных вычислений. Она представляет собой основу для понимания того, что можно вычислить, и формализует процесс вычислений. Хотя существуют и другие модели вычислений, машина Тьюринга является наиболее известной и широко признанной. Кроме того, Тьюринг описал принципы работы этой модели до появления первых компьютеров, что подчеркивает её значимость для развития информатики и теории вычислений.

Конечно, я готов помочь с редактированием текста. Пожалуйста, предоставьте исходный текст, который вы хотите переделать.

Его автомобили служили мостом, соединяющим абстрактные символы с физической реальностью.

Эндрю Ходжес в своей книге «Алан Тьюринг: Энигма» подробно описывает жизнь и достижения выдающегося математика и логика Алана Тьюринга. Тьюринг, считающийся одним из основоположников современных компьютерных наук, сделал значительный вклад в разработку теорий, которые легли в основу искусственного интеллекта и алгоритмов. В биографии Ходжеса освещены как научные достижения Тьюринга, так и его личная жизнь, включая трудности, с которыми он столкнулся в обществе. Книга является важным ресурсом для тех, кто интересуется историей вычислительных технологий и жизнью выдающихся личностей, оказавших влияние на развитие науки. Чтение этого произведения позволяет глубже понять не только научные идеи Тьюринга, но и контекст его времени, что делает его незаменимым источником для студентов, исследователей и всех, кто интересуется наследием этого гениального ученого.

Новаторство Алан Тьюринга заключалось в использовании двоичной системы счисления в своей машине в то время, когда в основном применялась десятичная система. Для большинства людей в 1936 году двоичные числа были малознакомы. Например, компьютер ENIAC, созданный в 1943-1945 годах, использовал десятичную систему. Термин «бит», который является сокращением от binary digit («двоичная цифра»), появился в научной литературе только в 1948 году. Таким образом, вклад Тьюринга стал основой для будущих вычислительных технологий, формируя представление о том, как должна функционировать современная компьютерная техника.

Автоматическая машина, которая печатает два типа символов, из которых первый тип, состоящий исключительно из 0 и 1, называется цифрами, а второй тип включает другие символы, классифицируется как вычислительная машина. Важность таких машин заключается в их способности обрабатывать и хранить информацию, что делает их основой современных вычислительных устройств и технологий. Вычислительные машины играют ключевую роль в обработке данных и автоматизации процессов, что значительно упрощает выполнение сложных задач.

Алан Тьюринг в своей работе «О вычислительных числах, с приложением к проблеме принятия решений» рассматривает фундаментальные аспекты теории вычислений. Он анализирует концепцию вычисляемых чисел и вводит понятие алгоритма, что стало основой для дальнейшего развития информатики и теории вычислений. Тьюринг также обсуждает проблему принятия решений, показывая, как можно формализовать вычислительные процессы и их ограничения. Его исследования положили начало современным представлениям о машинах Тьюринга, которые играют ключевую роль в понимании вычислимости и алгоритмической сложности. Работа Тьюринга является важным вкладом в математику и компьютерные науки, оказывая влияние на последующие исследования в области искусственного интеллекта и теории информации.

Работа Алана Тьюринга имеет огромное значение, поскольку он предложил концепцию универсального компьютера общего назначения. Эта идея стала революционной, так как в то время компьютеры создавались для выполнения конкретных задач. Например, в 1920-х годах Вэнивар Буш и его студенты разработали аналоговый компьютер, известный как дифференциальный анализатор, который мог решать лишь обыкновенные дифференциальные уравнения и выполнял только эту узкую функцию. Тьюринг же открыл путь к созданию многофункциональных компьютеров, способных решать широкий спектр задач, что стало основой для дальнейшего развития вычислительной техники.

Разработка множества специализированных машин для выполнения различных вычислительных задач не является необходимостью. Все эти операции можно эффективно реализовать с помощью одного цифрового компьютера, который будет правильно запрограммирован для каждого конкретного случая. Такой подход обеспечивает универсальность и гибкость в решении вычислительных задач, снижая затраты и упрощая процесс разработки. Использование программируемого цифрового компьютера позволяет адаптировать его функциональность под различные требования, что делает его идеальным инструментом для современных вычислительных процессов.

Алан Тьюринг в своей работе «Вычислительная техника и интеллект» исследует взаимосвязь между вычислительными системами и человеческим разумом. Он анализирует, как машины могут имитировать интеллектуальное поведение человека и ставит под сомнение традиционные представления о разуме и интеллекте. Тьюринг вводит концепцию, известную как «Тест Тьюринга», который служит критерием для оценки способности машин к мышлению. В своей статье он также обсуждает возможности и ограничения вычислительных машин, подчеркивая, что хотя они могут выполнять множество задач, человеческое сознание остается уникальным и сложным явлением. Работа Тьюринга оказала значительное влияние на развитие искусственного интеллекта и продолжает оставаться актуальной в современных дискуссиях о границах вычислительных технологий и их способности к интеллектуальному функционированию.

На сегодняшний день не существует более эффективной модели вычислений, чем машина Тьюринга. Она позволяет определить минимальные условия, необходимые для выполнения любых вычислений, и тем самым выявляет ограничения современных компьютеров. Если определённое вычисление возможно на машине Тьюринга, то его можно выполнить и на любом другом вычислительном устройстве. Это свойство называется «полнота по Тьюрингу». Понимание этой концепции является ключевым для изучения теории вычислений и разработки новых алгоритмов.

Полнота по Тьюрингу

Полнота по Тьюрингу является ключевым понятием в информатике. Язык программирования или компьютер, который обладает свойством полноты по Тьюрингу, способен эмулировать машину Тьюринга. Это означает, что такой язык может выразить все вычислимые задачи, которые могут быть решены с помощью компьютеров. В большинстве случаев языки программирования считаются Тьюринг-полными, если не учитывать ограничения, связанные с объемом доступной памяти. Полнота по Тьюрингу важна для понимания теоретических основ вычислений и разработки программного обеспечения.

Java и C++ позволяют создавать программы, которые функционируют как машины Тьюринга, демонстрируя их полную вычислительную мощь. Полноту также характеризуют HTML5 и CSS3, которые обеспечивают обширные возможности для веб-разработки. В отличие от них, SQL не является полным языком программирования, так как предназначен в основном для написания запросов к базам данных, а не для создания полноценных программных решений.

Примеры реализации

Хотя данная разработка является мысленным экспериментом, нашлись энтузиасты, которые предприняли попытку создать её физический прототип. Эти усилия подчеркивают интерес и стремление к реализации инновационных идей, что может способствовать дальнейшему развитию технологии. Реализация таких проектов может открыть новые горизонты в области научных исследований и практических применений.

Ричард Ридел создал одну из самых впечатляющих моделей, на что у него ушло шесть месяцев. Этот трудоемкий процесс продемонстрировал его мастерство и внимание к деталям.

Некоторые разработчики создали модель машины Тьюринга, используя возможности Excel. Эта реализация позволяет продемонстрировать основные принципы вычислений и алгоритмов, которые лежат в основе теории вычислений. Использование Excel для моделирования машины Тьюринга не только делает концепцию более доступной, но и помогает лучше понять, как работают алгоритмы и логика вычислений. Такой подход может быть полезен как для студентов, изучающих информатику, так и для профессионалов, интересующихся вычислительными процессами. Модель в Excel позволяет экспериментировать с различными состояниями и правилами, что открывает новые горизонты для изучения теории автоматов и вычислительных систем.

При чём тут грибы?

Машина Тьюринга, разработанная почти столетие назад, по-прежнему актуальна и востребована в современных исследованиях. Робототехник Джошуа Бонгард и биолог Майкл Левин в своих работах предлагают расширить наше восприятие вычислительных систем, включая в этот контекст не только традиционные компьютеры, но и живые организмы. Их подход открывает новые горизонты в изучении вычислительных процессов, что может привести к значительным прорывам в области биоинформатики и робототехники.

Данное определение охватывает разнообразные сущности, которые не являются традиционными компьютерами. В этот список входят такие живые организмы, как стаи крабов и грибы, а также неорганические вещества, например жидкости, и даже алгоритмы, функционирующие внутри других компьютеров.

Джошуа Бонгард и Майкл Левин в своей работе «Здесь много места: биологические системы как эволюционировавшие, перегруженные, многомасштабные машины» исследуют сложные биологические системы, рассматривая их как результат эволюционного процесса. Авторы подчеркивают, что биология представляет собой многослойную структуру, в которой взаимодействуют различные уровни организации. Они акцентируют внимание на том, как эти системы способны адаптироваться и эволюционировать под воздействием различных факторов окружающей среды. Исследование Бонгарда и Левина открывает новые горизонты в понимании биологических механизмов и их потенциального применения в таких областях, как биоинженерия и экология. Эта работа способствует более глубокому осмыслению того, как природа создает сложные системы, которые могут служить образцом для разработки новых технологий и подходов в науке.

Для определения, могут ли крабы быть классифицированы как компьютеры, учёные рассматривают их в контексте машины Тьюринга. Однако в этом процессе возникают определённые трудности. Например, в случае с грибами или жидкостями сложно установить, что именно соответствует ленте, считывающей головке и программе. Это затрудняет анализ и понимание их функциональности в сравнении с традиционными вычислительными системами.

Система, представляющая собой машину Тьюринга, может показаться сложной для анализа, особенно когда речь идет о выделении её отдельных компонентов, таких как лента и считывающая/записывающая головка. Это затрудняет понимание её работы и функциональности, так как все элементы взаимосвязаны и функционируют совместно. Понимание этих компонентов и их взаимодействия необходимо для глубокого анализа вычислительных процессов и теоретических основ информатики.

Джошуа Бонгард и Майкл Левин в своей работе «Здесь много места: биологические системы как эволюционировавшие, перегруженные, многомасштабные машины» исследуют сложность биологических систем и их эволюцию. Авторы рассматривают, как различные уровни организации живых организмов взаимодействуют и адаптируются в изменяющихся условиях окружающей среды. Они акцентируют внимание на многомасштабности биологических машин, подчеркивая значимость этих систем для понимания эволюционных процессов и биологической устойчивости. Эта работа открывает новые горизонты для научных исследований и углубленного анализа механизмов, лежащих в основе жизни.

Биологические системы подвержены эволюции и со временем претерпевают изменения, что делает сложным использование строгих математических определений для их описания. Эти динамичные процессы требуют гибкого подхода, поскольку биология представляет собой непрерывно развивающуюся область, где изменения происходят на различных уровнях, от молекулярного до экосистемного. Эволюция биологических систем демонстрирует их адаптивную природу, что усложняет создание универсальных математических моделей. Важно учитывать, что для точного анализа биологических процессов необходимо применять более комплексные и адаптивные методы, которые смогут отражать их многообразие и изменчивость.

Конечно, я готов помочь с редактированием текста. Пожалуйста, предоставьте сам текст, который вы хотите переделать.

Такое поведение усложняет не только формулировку вопроса: «Является ли это компьютером?», но и затрудняет любые попытки определить, в какой момент система начинает функционировать как компьютер.

Джошуа Бонгард и Майкл Левин в своей работе «Здесь много места: биологические системы как эволюционировавшие, перегруженные, многомасштабные машины» исследуют биологические системы с точки зрения их эволюции и сложности. Авторы подчеркивают, что организмы представляют собой многоуровневые машины, которые развивались на протяжении миллионов лет, адаптируясь к разнообразным условиям окружающей среды. В книге рассматриваются механизмы, благодаря которым такие системы могут справляться с различными нагрузками и изменениями, а также влияние многомасштабности на их функциональность. Работа Бонгарда и Левина открывает новые горизонты для понимания биологии и эволюции, предлагая свежий взгляд на то, как организмы взаимодействуют с окружающим миром и как они могут быть рассмотрены как сложные системы, которые продолжают эволюционировать.

На сегодняшний день машина Тьюринга остается одним из самых эффективных концептов в области вычислений. Поэтому Бонгарду и Левину предстоит разобраться, где у крабов расположена лента, а также определить, где находится считывающая головка. Исследование этих элементов может помочь в дальнейшем понимании принципов работы вычислительных систем и их аналогов в природе.

Изучите также:

• PARC компьютерного периода: кто, где и как создавал технологии современности
• Революция транзисторов: от механических машин к суперкомпьютерам будущего
• Что такое алгоритмы и какими они бывают