Что такое математическое мышление / Skillbox Media

Содержание:

• Что такое математическое мышление
• Как развивать математическое мышление
• Что делать, если отношения с математикой не сложились
• Зачем вообще нужно учиться математике

Профессор-ассистент в Университете Утрехта, Нидерланды, и кандидат психологических наук. В своей диссертации, защищенной в МГУ имени М. В. Ломоносова, исследовала влияние чувственных представлений на усвоение математических понятий. Является автором курса по математике для начальной школы на платформе «Учи.ру» и консультировала разработку заданий для «Яндекс Учебника».

Что такое математическое мышление

Термин «математическое мышление» относится к способности анализировать, обобщать и решать проблемы с использованием математических концепций и методов. Это включает в себя умение формулировать и структурировать задачи, применять логические рассуждения и использовать математический язык для описания и решения различных явлений. Математическое мышление развивает критическое мышление и способствует более глубокому пониманию окружающего мира, позволяя людям делать обоснованные выводы и принимать решения на основе анализа данных. Важно отметить, что математическое мышление не ограничивается лишь выполнением вычислений, но охватывает целый ряд навыков, включая абстрактное и пространственное мышление. Развитие этих навыков может значительно повысить успех в учебе и в профессиональной деятельности, так как они применимы в самых разных областях, от науки до экономики и инженерии.

Существует множество определений математического мышления, так как эта тема изучается в рамках двух основных научных направлений. Первое направление — когнитивная наука, которая фокусируется на процессах познания и понимания. Второе направление — наука о математическом образовании, исследующая методы и подходы к обучению математике. Эти два научных сообщества имеют разные подходы и идеи, что приводит к разнообразию в понимании того, как человек мыслит в области математики.

Термин можно определить как мышление в контексте культурной практики математики. В различных сферах деятельности сформировались уникальные культурные практики, которые отличаются своими стратегиями мышления. Каждая область имеет свои особенности, влияющие на подходы к решению задач и развитию математических концепций.

Мышление, включая такие процессы, как планирование, рассуждение и обоснование, варьируется в зависимости от дисциплины. В физике, географии и математике оно строится на специфических методах и подходах, которые характерны для каждой из этих областей. В то же время в искусстве, например, в танце или живописи, мышление проявляется через другие культурные практики и творческие процессы. Каждая из этих сфер требует уникальных навыков и способов интерпретации, что делает их изучение и практику разнообразными и интересными.

Существует альтернативный подход к пониманию математического мышления. Этот подход акцентирует внимание на процессе решения задач и разработке логических стратегий, а не только на использовании формул и теорем. Математическое мышление включает в себя способности к анализу, синтезу и критическому мышлению, что позволяет находить нестандартные решения и применять математические идеи в различных контекстах. Такой подход способствует развитию креативности и гибкости ума, что является важным аспектом в обучении математике и в дальнейшем использовании математических знаний в жизни.

Математика является обширной культурной практикой и занимает значительное место в иерархии человеческой деятельности и наук. Эту важность можно наблюдать, например, в различии зарплат между профессиями, где требуется математическая подготовка, и теми, где она не является необходимой. Поэтому математика занимает важную роль в школьной программе, и образовательное сообщество активно стремится развивать это направление.

Математическое мышление считается основополагающим навыком, который тесно связано с логикой и способностью к рассуждению. Это умение позволяет анализировать, обобщать и решать сложные задачи, что делает его важным для развития критического мышления. Математическое мышление не только способствует успешному изучению математики, но и помогает в других областях, таких как физика, экономика и информатика. Развитие этого навыка открывает новые горизонты для понимания окружающего мира и принятия обоснованных решений в повседневной жизни.

Существует мнение, что математическое мышление является отдельной сущностью, которую можно развивать независимо от изучения математики как предмета. Это создает ожидание, что развитие математического мышления окажет положительное влияние на другие сферы жизни. На самом деле математическое мышление включает в себя логическое и аналитическое мышление, что делает его важным не только для математики, но и для решения задач в различных областях, таких как физика, экономика и информатика. Развитие этих навыков может способствовать улучшению общей способности к решению проблем и принятию обоснованных решений в повседневной жизни.

В настоящее время в науке широко распространено понимание, что многообразие подходов и интерпретаций играет ключевую роль в развитии знаний. Научные исследования становятся все более междисциплинарными, что позволяет интегрировать различные теории и методы. Это способствует более глубокому пониманию сложных явлений и процессов. Исследователи стремятся к более открытым и гибким моделям, которые учитывают разнообразие мнений и данных. Такой подход укрепляет научное сообщество и помогает находить новые пути для решения актуальных проблем.

В отечественной психологии на протяжении длительного времени наблюдался тренд на обширное понимание математического мышления. Оно рассматривалось как способность к обобщению и логическому рассуждению, что подчеркивало важность этих навыков в процессе анализа и решения задач. В этом контексте математическое мышление стало ассоциироваться не только с конкретными вычислительными навыками, но и с общей способностью к логическому анализу и критическому мышлению, что является основополагающим в образовательном процессе и научной деятельности.

Современная западная наука акцентирует внимание на интеграции математического обучения с другими дисциплинами, особенно в рамках STEM — направления, охватывающего естественные науки, технологии, инжиниринг и математику. Психологи образования подчеркивают важность понимания математического мышления как инструмента для решения реальных жизненных задач. Это подход способствует более глубокому усвоению математических концепций и их практическому применению, что делает обучение более значимым и эффективным.

На протяжении XX века взгляд на математику претерпел значительные изменения. Математика стала отделяться от практических аспектов жизни, что отразилось на подготовке специалистов в этой области. В частности, в олимпиадном движении акцент делался на развитие узкоспециализированных навыков, которые часто не находят применения в реальных жизненных ситуациях. Это отделение математики от её практического использования поднимает вопрос о необходимости интеграции математических знаний в повседневную жизнь и решение актуальных задач.

Математика долгое время воспринималась как предмет для избранных, доступный лишь немногим. В настоящее время наблюдается активная попытка пересмотра подходов к обучению математике. Этот тренд находит отражение в крупных международных исследованиях, таких как PISA и TIMSS, которые анализируют уровень образования школьников в разных странах. Современные методы обучения направлены на то, чтобы сделать математику более доступной и интересной для всех учащихся, что способствует улучшению общего уровня знаний и навыков в этой важной области.

Как развивать математическое мышление

Изучение математики в школах сосредоточено на освоении чётких правил, понятий и методов решения задач. Однако этого может быть недостаточно для полноценного развития математического мышления. Важно не только запоминать алгоритмы и формулы, но и понимать их логику, а также развивать аналитические способности. Для достижения глубокого понимания математики необходимо интегрировать теорию с практическими задачами, что поможет учащимся осознать, как математика применяется в реальной жизни. Такой подход способствует формированию критического мышления и творческого подхода к решению проблем, что является ключевым аспектом в обучении математике.

Математические задачи можно классифицировать на рутинные и творческие. Рутинные задачи имеют четко определенный набор действий, которые необходимо выполнить для их решения. Чтобы успешно справиться с такими задачами, важно сначала определить их тип, а затем следовать заданному алгоритму. Творческие задачи, в отличие от рутинных, требуют нестандартного подхода и оригинального мышления.

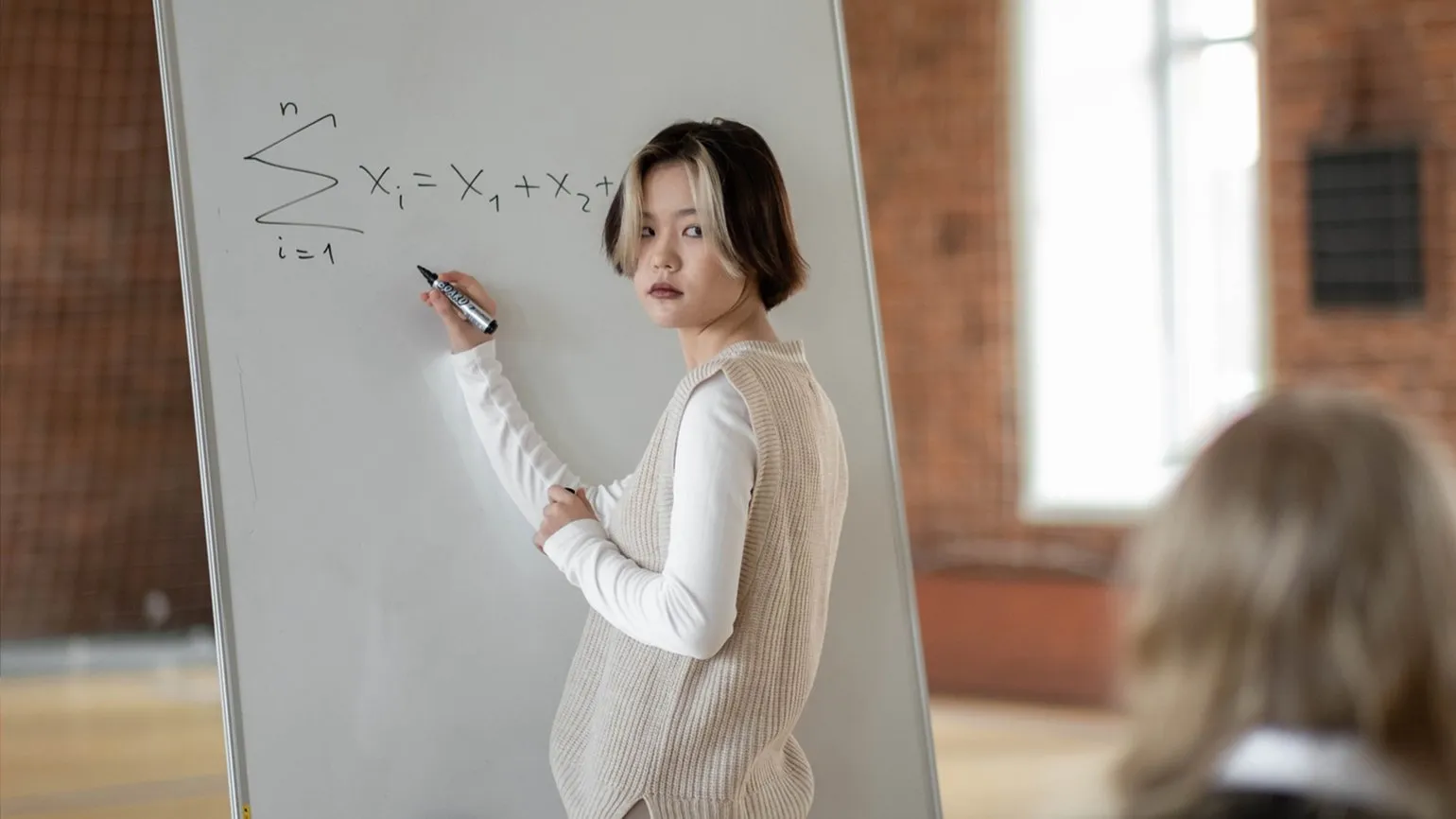
Школьные программы по всему миру в значительной степени сосредоточены на обучении рутинным задачам. Однако такие навыки не могут считаться истинным мышлением. Мышление — это процесс поиска решений без заранее заданного алгоритма. Выученные действия, основанные на правилах, не следует относить к математическому мышлению. Важно развивать у учащихся способности к критическому анализу и творческому подходу к решению задач. Это позволит формировать более глубокое понимание математики и развивать навыки, необходимые для решения нестандартных проблем.

Математическое мышление начинается с раннего возраста и активно развивается в процессе обучения. Оно включает в себя способность анализировать, обобщать и решать задачи, что является основой для успешного освоения математики. Важно стимулировать интерес к математике у детей через игры, задачи и практические примеры. Это помогает формировать логическое мышление и навыки решения проблем, которые пригодятся не только в учебе, но и в повседневной жизни. Развитие математического мышления может начаться уже в детском саду и продолжаться на протяжении всей школьной программы, а также за её пределами.

Когда мы говорим о применении математических понятий, возникает важный вопрос: что именно мы подразумеваем под математическим понятием? Математические понятия являются основой для решения задач и понимания математических теорий. Они формируют базу для изучения более сложных тем и являются инструментами, которые помогают анализировать и интерпретировать различные явления. Определение и понимание математических понятий играют ключевую роль в обучении математике и развитии аналитического мышления.

Тригонометрическая функция — это не просто определение, а целый комплекс различных моделей. К ним относятся алгебраические выражения, представления через треугольники и единичные окружности, а также графические изображения. Для глубокого понимания тригонометрических функций и их применения в математике необходимо освоить сложные действия с разнообразными объектами. Это позволит не только осознать их природу, но и эффективно использовать в решении математических задач.

Формальные операции можно записать в виде алгоритмов и легко изучить, однако овладение визуальными моделями требует другого подхода. Это не просто искусство, а сложная практика, которую невозможно полностью формализовать. Научиться ей можно только через опыт, пробуя и совершая ошибки. Примером может служить то, как дети осваивают использование вилки и ножа или учатся кататься на велосипеде. Невозможно овладеть этой практикой лишь через чтение теоретических материалов.

Выученные определения и алгоритмы сами по себе не приводят к полноценному пониманию предмета. Просто «выучить» не означает «овладеть» или «уметь применить» на практике. Существует явление, известное как вербализм, при котором ученик может произнести определение, но не в состоянии распознать соответствующий объект. Например, учащийся может точно формулировать, что прямоугольный треугольник — это треугольник с прямым углом. Однако, если он увидит прямой угол в необычном контексте, он не сможет идентифицировать этот треугольник. Таким образом, знание определений, свойств и правил не гарантирует развитие критического мышления и способности к практическому применению знаний. Важно не только запоминать информацию, но и уметь её использовать в различных ситуациях для достижения глубокого понимания.

Умение решать творческие задачи и мыслить в области математики невозможно без освоения алгоритмов и правил. Эти основы служат фундаментом для дальнейшего развития навыков. Важно, чтобы в школьной программе было оптимальное соотношение рутинных и нерутинных задач. Рутинные задачи помогают закрепить базовые навыки, тогда как нерутинные развивают креативное мышление и способность к решению нестандартных проблем. Эффективная программа должна сочетать оба типа задач, чтобы обеспечить всестороннее развитие учащихся.

Для успешного освоения математики у детей должна быть sólida база знаний. Важно, чтобы они уверенно считали в пределах ста и свободно пользовались таблицей умножения. Эти навыки являются необходимыми пререквизитами для дальнейшего изучения более сложных математических концепций. Углубленное понимание математики невозможно без основательного освоения базовых арифметических операций, что поможет детям уверенно справляться с более сложными задачами в будущем.

Традиционные методы обучения не обеспечивают необходимую гибкость для решения более сложных задач. Например, при изучении таблицы умножения ребёнок может запомнить, что «шесть на восемь — сорок восемь». Однако для успешного решения задач, связанных с этими числами, важно понимать, что 48 можно представить не только как 6 умножить на 8, но и как 12 умножить на 4 или другими способами. Это понимание помогает развивать математическое мышление и улучшает навыки решения задач.

Необходима определённая «напитанность» и насыщенность числовым материалом, а не просто механическое запоминание. Здесь можно упомянуть понятие ловкости. Ловкость в движении аналогична ловкости в счёте. Это подразумевает, что счёт может осуществляться различными способами, и важно уметь выбирать наиболее удобный подход в каждой конкретной ситуации. Базовые навыки следует развивать не как набор фиксированных алгоритмов, а как гибкий и адаптивный навык.

Тренировка и повторение простых действий действительно необходимы, но не обязательно в традиционном формате. Важно найти эффективные методы, которые помогут усвоить навыки без излишней рутины. Использование разнообразных подходов может значительно повысить эффективность процесса обучения. Это позволит не только лучше запомнить информацию, но и сделать занятия более интересными и продуктивными.

Тренировка действительно важна, но она должна основываться на гибкости и решении задач, а не на простом заучивании. Эффективный подход к обучению включает в себя развитие критического мышления и способность адаптироваться к новым условиям. Использование задач и практических заданий позволяет не только укрепить знания, но и повысить уровень понимания материала.

Второй важный аспект, который я хотел бы обсудить, связан с привычкой воспринимать мир через призму математики. Я способен оценить объем воды, который использую за день, рассчитать продолжительность поездки или определить оптимальный маршрут для похода за покупками, учитывая как стоимость, так и временные затраты. Все эти повседневные задачи являются принципиально нестандартными и не имеют четкого алгоритма выполнения.

Когда мы начинаем обучать детей пошаговым алгоритмам, важно отметить, что их способность замечать моменты, когда математическая практика может быть полезной, часто ослабевает или вовсе не формируется. В результате возникает различие между школьной математикой и уличной математикой. Школьная математика фокусируется на формальных методах и алгоритмах, в то время как уличная математика относится к практическому применению математических знаний в повседневной жизни. Это различие подчеркивает необходимость интеграции практических задач в образовательный процесс, чтобы развить у детей не только теоретические знания, но и навыки их применения в реальных жизненных ситуациях.

Человек, обладающий навыками уличной математики, может не иметь знаний, полученных в школьной системе. Уличная математика включает в себя практические навыки и умения, которые развиваются в повседневной жизни и реалиях, а не через традиционное образование. Эти навыки могут быть полезны в различных ситуациях, таких как расчет бюджета, оценка расстояний и решение задач на основе жизненного опыта. Таким образом, уличная математика и школьная математика могут существенно отличаться по своему содержанию и применению.

В Индии проведено множество исследований, касающихся навыков счёта у детей. На улицах они активно торгуют и демонстрируют отличные способности в работе с числами и примерами. Однако, когда эти же дети оказываются в школе, они сталкиваются с трудностями. У них отсутствует связь между реальными жизненными ситуациями и теми заданиями, которые им предлагают в учебном процессе, такими как «сделай А, сделай B, сделай C». Это подчеркивает важность адаптации образовательных методов к реальным потребностям детей, чтобы они могли успешно применять свои знания в повседневной жизни.

В 1990-е годы возникли обсуждения о том, что перенос знаний и навыков на самом деле не существует, а является лишь концепцией, вымышленной психологами. Для того чтобы ребенок смог перенести свои рассуждения из знакомых условий на новые ситуации, ему необходимо сначала увидеть их как похожие. Однако распознавание школьной ситуации, представленной в тетрадке, и реальной жизненной ситуации за пределами учебного заведения как похожих представляется практически невозможным, поскольку на первый взгляд они существенно различаются.

Узнайте больше о процессе переноса знаний и навыков из одной области в другую. Этот метод позволяет эффективно применять уже имеющиеся компетенции в новых контекстах, что способствует развитию профессиональной гибкости и повышению конкурентоспособности на рынке труда. Перенос знаний также открывает новые возможности для обучения и самосовершенствования. Читайте далее, чтобы глубже понять преимущества этого подхода и его практическое применение в различных сферах.

Когнитивная психология — это область психологии, которая фокусируется на изучении умственных процессов, таких как восприятие, мышление, память и обучение. Она играет ключевую роль в образовательной сфере, так как помогает понять, как студенты воспринимают информацию, как они её обрабатывают и как формируют знания.

Понимание когнитивных процессов позволяет разработать эффективные методы обучения, которые соответствуют особенностям восприятия и обработки информации у различных учеников. Например, когнитивная психология помогает определить, какие стратегии обучения наиболее эффективны для запоминания материала и решения задач.

Кроме того, знания в области когнитивной психологии способствуют созданию адаптивных образовательных программ, которые учитывают индивидуальные особенности учащихся. Это особенно важно в контексте инклюзивного образования, где необходимо учитывать разнообразие подходов к обучению.

Таким образом, когнитивная психология не только углубляет наше понимание механизмов обучения, но и способствует улучшению образовательных практик, что в итоге ведет к повышению качества образования.

Некоторые дети способны решать задачи, с которыми они ранее не сталкивались. Это может быть связано не только с их врождёнными способностями, но и с развитием логического мышления, креативности и умением анализировать информацию. Такие навыки могут формироваться в процессе обучения и взаимодействия с окружающей средой. Важно создать условия, способствующие развитию этих качеств, чтобы дети могли успешно справляться с новыми вызовами.

Психогенетические исследования показывают наличие определённых факторов наследуемости, однако они часто не учитывают взаимодействие генетических и экологических факторов. Если существуют так называемые «математические гены», то ребёнок, унаследовавший их, растёт в среде, где родители вовлекают его в обсуждения, связанные с математикой. Например, они могут спрашивать: «Справедливо ли нам посчитали сдачу в магазине?» или «Хватит ли 100 рублей на мороженое и черешню?» Это подчеркивает, что генетика и окружающая среда находятся в тесной взаимосвязи. Поэтому определить, что является врождённым, а что формируется под влиянием семейных практик, крайне трудно. Понимание этой взаимосвязи имеет важное значение для дальнейших исследований в области психогенетики и воспитания.

Как профессионал в области образования, я не считаю, что следует акцентировать внимание на вопросе врождённости способностей. Утверждение, что способности определяются исключительно генетически, снимает с образовательного сообщества ответственность за развитие каждого ученика, что является ошибочным подходом. Каждый ребёнок способен многому, если ему предоставлены необходимые условия и поддержка для обучения. Создание подходящей образовательной среды играет ключевую роль в раскрытии потенциала учащихся и формировании их навыков.

Если способности ребенка развиваются в подходящей среде в дошкольном возрасте, это может положительно сказаться на его успехах в школе, особенно в математике. Дошкольное обучение, основанное на игре и взаимодействии, способствует формированию фундаментальных навыков, таких как логическое мышление, пространственное восприятие и базовые математические понятия. Эти навыки облегчают понимание более сложных математических тем в школьной программе. Поэтому раннее развитие в поддерживающей среде может значительно повысить шансы ребенка на успех в учебе.

Фундаментальным фактором в обучении детей математике является мотивация. Когда маленький ребёнок начинает осваивать счёт, например, помогая накрыть стол, он считает, сколько вилок и ложек нужно для гостей. Этот процесс приносит ему радость и удовлетворение. Положительные эмоции, которые он вызывает у родственников, усиливают его желание учиться и осваивать математические навыки. Таким образом, мотивация играет ключевую роль в формировании у ребёнка интереса к математике и в его дальнейшем обучении.

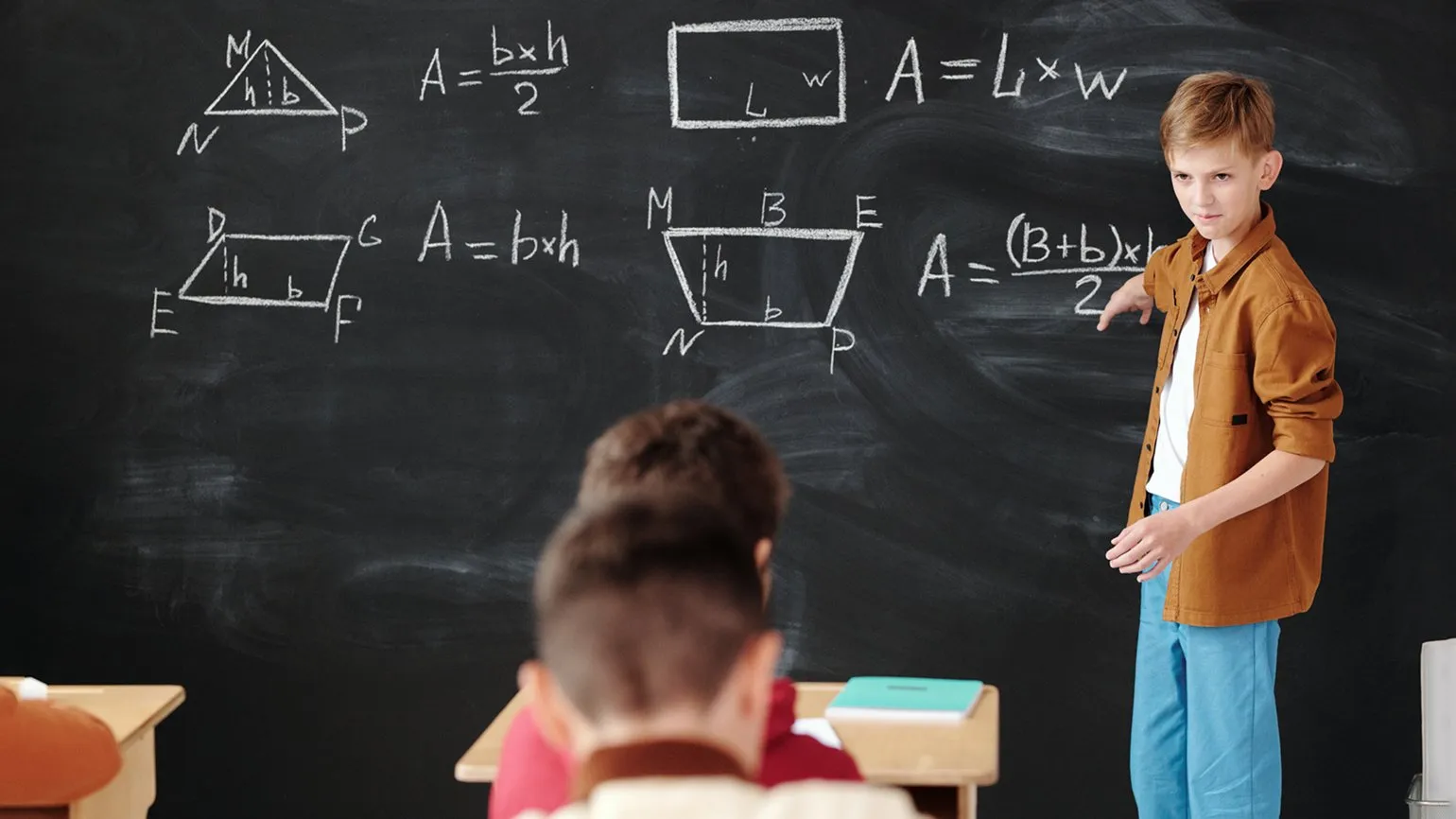
Что происходит в школе? Мы в «Учи.ру» провели глубокий анализ программ начальной школы и сделали важные выводы. Например, когда в первый класс приходит ребёнок, который уже умеет считать до десяти или даже до двадцати, его вновь учат считать до десяти. Это создает ситуацию, когда ученикам приходится повторять знакомый материал, что может негативно сказаться на их мотивации и интересе к учебе. Более эффективный подход в обучении начал бы с учета уже имеющихся у детей знаний, что позволило бы развивать их навыки дальше и углублять понимание чисел и арифметики.

Многие дети проводят полгода или даже год на уроках математики, не испытывая интереса и скучая. Во втором классе начинается появление более интересных задач, однако они всё еще достаточно просты и воспринимаются без особых усилий. Но далее, в третьем и четвёртом классах, программа резко усложняется. Задачи становятся значительно сложнее, и именно в этот момент мы теряем огромное количество детей, которые не справляются с новыми требованиями. Это создает серьезную проблему для дальнейшего обучения математике и формирования положительного отношения к этому предмету.

Многим школьникам оказывается трудно совершить переход к более сложным математическим концепциям. У них отсутствует естественная мотивация и желание преодолевать математические трудности, так как интерес, который был ранее, подавлен скучными уроками из предыдущих лет. Это приводит к тому, что ученики теряют уверенность в своих силах и не могут успешно справляться с новыми задачами. Важно создать атмосферу, способствующую развитию интереса к математике и стимулирующую учащихся на преодоление трудностей.

Что делать, если отношения с математикой не сложились

Многие школьники сталкиваются с резким увеличением сложности математических задач, что становится одной из причин, по которой они начинают сомневаться в своих способностях к математике. Этот переход к более сложным концепциям может вызвать у учащихся чувство неуверенности и привести к убеждению, что они не способны осваивать предмет. Понимание причин этой проблемы важно для разработки эффективных методов обучения и поддержки студентов в их математическом развитии.

Отношение школьников к математике является одним из самых поляризованных среди всех предметов. Исследования показывают, что лишь 20% детей проявляют любовь к этому предмету, в то время как 80% испытывают негативные чувства. Это указывает на то, что математика вызывает у учеников сильные эмоции, и многие из них относятся к ней крайне критически. Существует множество факторов, способствующих такому восприятию, включая сложность материала, методику преподавания и личные предпочтения учащихся.

Математика занимает особое место в образовательной системе, и её роль в формировании карьерных перспектив сложно переоценить. Исследования показывают, что существует высокая корреляция между уровнем математической подготовки и уровнем заработной платы. Люди с крепкими математическими навыками, как правило, получают значительно более высокие доходы. Это создает давление на детей с ранних лет, внушая им, что математика — это ключевой предмет, который определяет их будущее. Такое восприятие может привести к негативному отношению к математике в дальнейшем. Важно найти баланс между необходимостью изучения этого предмета и поддержкой интереса к нему, чтобы избежать отторжения и развить позитивное отношение к математике и её важности в жизни.

Для достижения оптимальных результатов в поисковых системах важно уделять внимание содержанию текста. Убедитесь, что ваш контент уникален, информативен и соответствует запросам пользователей. Включите ключевые слова, связанные с темой, чтобы улучшить видимость страницы. Также полезно использовать внутренние ссылки на другие релевантные материалы для создания связного контента и увеличения времени нахождения пользователей на сайте. Регулярно обновляйте информацию, чтобы она оставалась актуальной и полезной для вашей аудитории. Оптимизация заголовков и метаописаний также играет важную роль в SEO, поэтому не забывайте о них.

Математическая тревожность: понятие и методы преодоления

Математическая тревожность — это эмоциональное состояние, характеризующееся страхом и беспокойством перед выполнением математических задач и изучением математических дисциплин. Это явление может существенно повлиять на учебный процесс и общую успеваемость учащихся. Математическая тревожность часто возникает из-за недостатка уверенности в собственных математических способностях, негативного опыта в прошлом или отсутствия поддержки со стороны преподавателей и родителей.

Существует несколько эффективных методов борьбы с математической тревожностью. Во-первых, важно развивать уверенность в своих силах через регулярные занятия и практику. Решение простых задач и постепенное усложнение материала помогут укрепить математические навыки и снизить уровень тревожности.

Во-вторых, создание комфортной учебной среды также играет ключевую роль. Поддержка со стороны учителей и одноклассников, а также положительное отношение к ошибкам могут значительно снизить уровень стресса.

Кроме того, полезно применять различные техники релаксации, такие как дыхательные упражнения или медитация, которые помогут справиться с волнением перед контрольными работами и экзаменами.

Понимание своей тревожности и работа над ее преодолением способны значительно улучшить не только успеваемость в математике, но и общее отношение к предмету. Устранение математической тревожности открывает новые возможности для обучения и развития, позволяя каждому учащемуся раскрыть свой потенциал.

Популярность информационных технологий и IT-профессий оказывает значительное влияние на современное общество. В условиях быстрого развития технологий наблюдается рост спроса на квалифицированные кадры в сфере IT. Это приводит к повышению конкуренции среди специалистов и требует от них постоянного обновления знаний и навыков. Кроме того, информационные технологии становятся неотъемлемой частью бизнеса, что создает дополнительное давление на работников, стремящихся соответствовать высоким стандартам и ожиданиям работодателей. В итоге, изменения в IT-сфере не только формируют новые требования к профессиональным навыкам, но и влияют на карьерные перспективы и развитие рынка труда в целом.

Я рассматриваю это как положительный аспект, поскольку для успешного обучения IT-профессиям и программированию не требуется глубокое знание математики. Это создает дополнительные возможности для людей всех возрастов, включая взрослых, которые хотят освоить новые навыки и начать карьеру в сфере информационных технологий. Такой подход делает IT-образование более доступным и привлекательным для широкой аудитории.

Существует множество качественных курсов программирования для детей, которые благодаря своей инновационности избегают традиционного, рутинного и алгоритмического подхода к обучению. Эти курсы ориентированы на детское любопытство и предоставляют возможность исследовать и открывать новое. Они создают увлекательную образовательную среду, способствующую развитию творческих и аналитических навыков у молодых программистов. Выбор таких курсов поможет детям не только освоить основы программирования, но и развить критическое мышление и навыки решения проблем.

Для многих молодых людей программирование становится средством решения жизненных задач, включая увлечения, такие как игры. Например, они могут играть в Minecraft и стремиться улучшить игровой процесс для себя. Это можно сделать с помощью простого программирования. Таким образом, образование органично интегрируется в повседневную жизнь. Интерес к программированию не только развивает навыки, но и помогает взрослым преодолеть стресс, связанный с математикой.

Вопрос о том, можно ли интегрировать математику в свою жизнь во взрослом возрасте, становится все более актуальным. Математика играет ключевую роль в различных аспектах нашей повседневной жизни, и ее применение может значительно упростить решения многих задач. Во-первых, математика помогает развивать аналитическое мышление и улучшает навыки решения проблем. Это особенно полезно в профессиональной сфере, где логика и расчет необходимы для принятия обоснованных решений.

Во-вторых, многие аспекты финансовой грамотности, такие как управление бюджетом, инвестиции и планирование расходов, требуют базовых математических навыков. Понимание процентов, дробей и простых уравнений может помочь вам более эффективно управлять своими финансами.

Кроме того, существует множество ресурсов, которые могут помочь взрослым вернуть интерес к математике. Онлайн-курсы, приложения для изучения математики и образовательные видео делают процесс обучения доступным и увлекательным.

Таким образом, математика не только актуальна, но и необходима в жизни взрослого человека. Встраивание математических знаний в повседневные задачи может привести к более осознанным решениям и повысить качество жизни.

С возрастом давление «ты должен это знать» значительно снижается, что позволяет взрослым легче разбираться в различных вопросах. Это создает возможность для глубокого понимания и анализа информации, что особенно важно в современном мире, где знания и навыки обновляются с большой скоростью. Взрослые могут уделить больше времени осмыслению и изучению тем, которые их действительно интересуют, что способствует личностному и профессиональному развитию.

Порог входа в математику значительно выше. Если в школьные годы вы не изучали историю и позже решили восполнить этот пробел, сделать это не так сложно. Достаточно приложить усилия, выделить время, слушать лекции, разобраться в теме и запомнить важные моменты. В этом случае не потребуется осваивать новые навыки, что облегчает процесс обучения. Однако в математике ситуация иная. Здесь необходимо не только усвоение теории, но и развитие аналитического мышления, что требует большего времени и усилий. Поэтому для успешного изучения математики важно заранее осознать сложности и подготовиться к ним.

В математике важно достигнуть уровня свободного владения числовыми данными, алгебраическими формулами и визуальными представлениями. Это можно сравнить с навыком катания на велосипеде или коньках — для его освоения требуется практика. Без регулярной тренировки достичь высокого уровня владения математикой взрослым оказывается достаточно сложно. Поэтому необходимо уделять внимание постоянному обучению и практике, чтобы преодолеть трудности и уверенно применять математические знания в жизни.

В условиях активной цифровизации знаний математики стали особенно важными в областях, не связанных напрямую с наукой и техникой. С развитием технологий и увеличением объема данных, умение анализировать и обрабатывать информацию становится необходимым навыком. Математика помогает людям принимать обоснованные решения, рационально использовать ресурсы и оптимизировать процессы. В сфере бизнеса, маркетинга, финансов и даже в гуманитарных науках математические модели и статистические методы становятся основой для успешной работы. Таким образом, знание математики становится не просто полезным, а критически важным для профессиональной деятельности в современном мире.

Сейчас, по моему мнению, необходимость в знании математики снизилась. Это связано с тем, что все процессы, которые можно автоматизировать, уже автоматизированы. Живое общение, однако, не подлежит автоматизации. В современных условиях чаще не требуется производить вычисления в уме. Важно либо быть разработчиком автоматизированных систем, либо работать в профессиях, где основное внимание уделяется взаимодействию с людьми.

Многие математические знания могут стать менее актуальными в будущем. С развитием технологий и автоматизации определенные навыки могут утратить свою ценность. Однако основополагающие концепции и принципы математики останутся важными, поскольку они формируют базу для решения сложных задач и понимания окружающего мира. Математика играет ключевую роль в различных областях, таких как наука, инженерия и экономика. Поэтому, несмотря на изменения в потребностях рынка труда, фундаментальные математические знания будут по-прежнему необходимы для развития аналитического мышления и критического подхода к решению проблем.

Слово «компьютер» изначально обозначало людей, занимающихся вычислениями. В Соединенных Штатах эту роль исполняли чернокожие женщины, что ярко отражено в фильме «Скрытые фигуры». Со временем эта профессия ушла в прошлое, и современные технологии сделали многие традиционные методы, такие как логарифмическая линейка, ненужными. Интересно задуматься о том, сколько других устаревших математических знаний и навыков остается в современных учебных программах и как они влияют на наше понимание математики и технологий. Современная образовательная система сталкивается с вызовом адаптации содержания к нуждам студентов, учитывая стремительное развитие технологий и изменение требований к навыкам.

Существует научная дисциплина, известная как curriculum studies, которая исследует, какие новые элементы следует включить в школьную программу, а какие можно исключить, основываясь на анализе исторического развития общества и опросах различных специалистов. Например, длительное внимание, уделяемое вычислению столбиком в российской школьной программе, вызывает сомнения в своей целесообразности.

Читайте также:

Содержание образования в современной российской школе вызывает много вопросов и критики. Многие эксперты утверждают, что учебные программы устарели и не соответствуют требованиям современного общества. Необходимость обновления образовательных методик становится все более очевидной, так как современные школьники сталкиваются с вызовами, которые требуют новых знаний и навыков.

Современная российская школа должна адаптироваться к быстро меняющемуся миру, внедряя актуальные дисциплины и современные подходы к обучению. Важно акцентировать внимание на развитии критического мышления, креативности и цифровых навыков, которые будут востребованы на рынке труда в будущем.

Образовательные стандарты должны учитывать не только академические знания, но и практические навыки, которые помогут ученикам успешно социализироваться и интегрироваться в общество. Внедрение новых технологий и методов обучения, таких как проектная работа и интерактивное обучение, может значительно повысить интерес школьников к учебному процессу и подготовить их к реальным жизненным ситуациям.

Таким образом, модернизация содержания образования в российской школе является актуальной задачей, требующей комплексного подхода и активного участия всех заинтересованных сторон.

Зачем вообще нужно учиться математике

Математическое и логическое мышление представляют собой разные аспекты когнитивных способностей. Однако, занятия математикой могут значительно способствовать развитию логического мышления. Математика требует от человека умения анализировать, делать выводы и решать задачи, что напрямую связано с логическими процессами. Решение математических задач помогает развивать навыки критического мышления, учит строить логические связи и выявлять закономерности. Таким образом, регулярные занятия математикой не только улучшают математические навыки, но и способствуют общему развитию логики, что является важным для успешного обучения и повседневной жизни.

Решение математических задач представляет собой важное упражнение на логическое мышление и анализ многоступенчатых действий. В отличие от других учебных дисциплин, в математике такая тренировка происходит наиболее интенсивно. Поэтому дети, успешно справляющиеся с математическими задачами, зачастую демонстрируют высокие результаты в шахматах и программировании. Эти области требуют умения просчитывать несколько шагов вперед и анализировать возможные последствия, что становится основным навыком для достижения успеха.

Математика способствует развитию различных навыков, включая пространственное мышление. Занятия математикой улучшают способности к абстрактному мышлению, логическому рассуждению и решению проблем. Кроме того, они помогают развивать аналитические навыки, что позволяет лучше воспринимать и обрабатывать информацию. Математика также способствует улучшению концентрации и внимательности, что в свою очередь положительно сказывается на учебных достижениях в других областях. Все эти навыки являются важными не только в учебе, но и в повседневной жизни, а также в профессиональной деятельности.

История с решением математических задач довольно сложна. Некоторые люди, включая как детей, так и взрослых профессиональных математиков, предпочитают использовать визуальные модели для понимания и решения задач. Таким образом, визуализация становится для них естественным инструментом. В то же время существует немало тех, кто ориентируется на определения и алгебраические формулы, практически не прибегая к визуальным конструкциям. В результате, нагрузка на пространственное мышление и его развитие варьируется в зависимости от подхода к решению математических задач. Это подчеркивает важность разнообразия методов обучения и тренировки математических навыков, что может существенно повлиять на эффективность усвоения материала.

В групповых исследованиях наблюдается корреляция между математическим мышлением и пространственными способностями. Однако это не указывает на то, что одно из этих качеств способствует развитию другого. На индивидуальном уровне нельзя утверждать, что улучшение пространственных способностей приведет к росту математического мышления или наоборот. Это лишь означает, что среди детей, успешно решающих математические задачи, можно встретить тех, кто также демонстрирует хорошие результаты в задачах на пространственную ориентацию.

На сегодняшний день отсутствуют убедительные доказательства универсальной связи между изучением математики и развитием пространственного мышления. Исследования в этой области продолжаются, и результаты пока не предоставляют четких выводов о том, что занятия математикой напрямую способствуют улучшению способностей к пространственному восприятию.

Доказательства отсутствуют, и на индивидуальном уровне ситуация остается сложной. Визуальные модели чаще всего оказывают помощь на начальных этапах изучения темы, особенно для тех, кто испытывает трудности в математике. Для человека, который уже освоил предмет, изучение новой темы возможно и без использования визуальных моделей. Тем не менее, в случае возникновения трудностей такие модели могут оказаться весьма полезными, хотя не всегда это так.

Для того чтобы визуальная модель была полезной, необходимо уметь воспринимать её абстрактное содержание. Чтобы «увидеть математику» в визуальных материалах, требуется определённое усилие. Это может быть особенно сложно для студентов, испытывающих трудности в изучении математики, поскольку такая задача добавляет дополнительную когнитивную нагрузку. Поэтому важно развивать навыки визуального восприятия и абстрактного мышления, чтобы помочь учащимся более эффективно осваивать математические концепции.

Существует интересный феномен, когда маленькие дети, получая задание нарисовать модель, например, показать, что Вася выше Саши, а Саша выше Маши, начинают изображать персонажей с кудряшками и одеждой. Дети не способны изобразить лишь математические соотношения, что подчеркивает их склонность к визуализации и эмоциональной интерпретации информации. Это явление демонстрирует, как важно развивать у детей не только математические навыки, но и творческое мышление, позволяя им выражать свои идеи через искусство.

Для успешного восприятия абстрактного содержания в визуальных моделях необходимо развивать определенные навыки. Это включает в себя понимание структуры и элементов визуального представления, а также способность интерпретировать информацию, представленную в абстрактной форме. Освоение этих навыков поможет лучше воспринимать и анализировать данные, что, в свою очередь, улучшит общее понимание сложных концепций и идей.

Изучение математики действительно способствует развитию навыков быстрого анализа информации и принятию обоснованных решений в различных сферах жизни. Математические концепции и методы учат логическому мышлению, структурированию данных и выявлению закономерностей. Эти умения полезны не только в научной и профессиональной деятельности, но и в повседневной жизни. Способность оценивать риски, проводить анализ и использовать количественные данные помогает принимать более взвешенные решения. Таким образом, математика является важным инструментом, который развивает критическое мышление и аналитические способности, необходимые для успешной адаптации в быстро меняющемся мире.

Существует множество способов рассуждения, и каждый из них имеет свою ценность. Я считаю, что не стоит подчеркивать важность исключительно математического мышления. Каждый подход к решению задач и анализу информации уникален и может быть полезен в разных ситуациях.

Я стремлюсь к созданию сообщества, где навыки эмпатии, понимание исторического контекста и психосоматическая саморегуляция имеют такое же значение, как и аналитическое мышление. Искусственный интеллект уже демонстрирует выдающиеся способности в анализе информации, и в будущем эта тенденция только усилится. Важно развивать образовательные подходы, которые акцентируют внимание на этих важных навыках, чтобы они не уступали в значимости математическому мышлению.

Узнайте больше об образовании и актуальных новостях в нашем телеграм-канале. Подписывайтесь, чтобы не пропустить важную информацию и полезные материалы!

Обратите внимание на следующие рекомендации по улучшению вашего контента. Оптимизация текста под SEO включает использование ключевых слов и фраз, которые соответствуют теме и помогут вашему ресурсу занять более высокие позиции в поисковых системах. Не забывайте о важности создания уникального и информативного контента, который будет интересен вашим читателям. Стремитесь к естественному встраиванию ключевых слов в текст, избегая их избыточного использования. Также полезно добавлять внутренние ссылки на другие страницы вашего сайта, чтобы улучшить навигацию и увеличить время пребывания пользователей на ресурсе. Это поможет повысить его авторитет в глазах поисковых систем.

Читайте также:

• Теория множественного интеллекта Говарда Гарднера: что об этой концепции говорит наука
• 9 вопросов о том, как генетика влияет на развитие и обучение детей
• Необычная практика: что такое математическая «генеалогия» и зачем она нужна
• Математика в жизни: где нужна и как избежать