Алгоритмы сортировки для собеседований / Skillbox Media

Содержание:

• На какие вопросы нужно ответить перед сортировкой массива
• Как работает Bubble Sort
• Как работает Selection Sort
• Как работает Insertion Sort
• Что такое стабильность сортировки
• Что не учитывает O(n)
• Что почитать и посмотреть

Программный инженер, специализирующийся на разработке систем управления городской инфраструктурой для мегаполисов по всему миру. Основные направления работы включают разработку серверной части и проектирование баз данных. Активно делится опытом и новыми идеями в Twitter под ником @ValeriiZhyla.

Ссылки играют ключевую роль в веб-контенте, обеспечивая навигацию и доступ к дополнительной информации. Они помогают пользователям перемещаться по сайту и находить нужные ресурсы. Эффективное использование ссылок улучшает пользовательский опыт и способствует поисковой оптимизации. Важно учитывать как внутренние, так и внешние ссылки. Внутренние ссылки связывают страницы вашего сайта, что помогает поисковым системам индексировать контент. Внешние ссылки, указывающие на авторитетные источники, увеличивают доверие к вашему сайту. Оптимизация анкорного текста также важна: он должен быть информативным и релевантным. Включение ссылок в контент способствует повышению его ценности и улучшает видимость в поисковых системах. Правильное размещение ссылок и их количество могут значительно повлиять на рейтинг вашего сайта.

В этом материале мы обсудим алгоритмы сортировки: Bubble Sort, Insertion Sort и Selection Sort. Вы узнаете о принципах работы каждого из этих алгоритмов, а также их преимуществах и недостатках. Мы детально разберем каждый алгоритм по шагам, рассмотрим их базовые реализации и предложим возможные улучшения. Эти алгоритмы являются основой для понимания более сложных методов сортировки и помогут вам глубже разобраться в алгоритмической эффективности.

Данный текст подразумевает, что вы знакомы с терминами, такими как «сложность worst-case алгоритма по времени равна O(n^2)». В дальнейшем я буду использовать сокращения: Time Complexity — «сложность по времени», а Space Complexity — «сложность по памяти». Понимание этих понятий является важным аспектом в области алгоритмов и анализа их эффективности.

Если вы только начинаете изучение теории алгоритмов, рекомендуется сначала ознакомиться со статьей Валерия о Big O Notation. В этой статье доступно объясняется, что такое алгоритмическая сложность и как правильно её вычислять. Понимание Big O Notation является важным шагом для освоения алгоритмов и улучшения навыков программирования.

На какие вопросы нужно ответить перед сортировкой массива

При подготовке к сортировке элементов массива программисту следует учесть несколько ключевых вопросов. Во-первых, какой алгоритм сортировки будет использоваться? Существует множество алгоритмов, таких как быстрая сортировка, сортировка слиянием или пузырьковая сортировка, и выбор подходящего зависит от особенностей задачи и объема данных. Во-вторых, какой тип данных содержится в массиве? Сортировка чисел, строк или объектов может потребовать различных подходов. Также важно определить, нужно ли выполнять сортировку по возрастанию или убыванию. Еще одним важным аспектом является эффективность алгоритма: как быстро он сможет обработать массив при увеличении его размера? Наконец, стоит задуматься о необходимости сохранения исходного массива: требуется ли создать новый массив с отсортированными элементами или достаточно изменить существующий? Ответы на эти вопросы помогут программисту выбрать оптимальный подход к сортировке массива.

Сортировка оригинала — это метод, при котором исходный массив данных изменяется в процессе сортировки. Основной недостаток данного подхода заключается в потере первоначального состояния массива, что может быть критично в некоторых случаях. Ценность исходного массива зависит от конкретной задачи и контекста использования. Следует учитывать, что данный подход может приводить к нежелательным побочным эффектам, что делает его менее предпочтительным в ситуациях, где требуется сохранить исходные данные.

Использование подхода без создания копии массива позволяет значительно оптимизировать потребление памяти. В данном случае Space Complexity остается на уровне O(1), что является эффективным решением. Кроме того, отсутствие необходимости в копировании массива приводит к экономии времени, снижая Time Complexity на O(n). Это делает алгоритм более производительным и экономичным.

Сортировка копии (out-of-place) представляет собой метод, при котором не происходит изменения исходного массива. В этом случае отсутствуют побочные эффекты, однако сложность алгоритма как по времени, так и по памяти возрастает до O(n). Стоит отметить, что дополнительное O(n) времени, затрачиваемое на копирование, не так критично на фоне времени, необходимого для самой сортировки, которое может быть значительно больше. Тем не менее, дополнительная память в O(n) является серьезным ограничением для использования out-of-place алгоритмов, особенно в условиях ограниченных ресурсов.

Напишем функцию, которая эффективно переставляет два элемента местами по их индексам:

Функция swap() принимает массив и два индекса. Сначала она сохраняет значение элемента с индексом first_idx в переменной temp. Затем значение элемента с индексом snd_idx присваивается элементу с индексом first_idx. На этом этапе содержимое обоих элементов становится идентичным, а оригинальное значение из first_idx хранится в переменной temp. В заключение, мы присваиваем это значение элементу с индексом snd_idx. Таким образом, функция swap() эффективно меняет местами значения двух элементов в массиве.

Идентификаторы, упомянутые выше, широко применяются в программировании. Временные значения обычно сохраняются в переменной temp, что является сокращением от слова «temporary», то есть «временный». Сокращения fst и snd обозначают «first» и «second» соответственно. Также слово «индекс» часто представляется в виде idx, поскольку программисты стремятся использовать буквы экономно.

Начнем с того, что сравнение элементов массива — это важный этап в сортировке данных. Но что делать после того, как вы провели сравнение? Правильно, менять элементы местами. Этот процесс может значительно улучшить порядок в массиве и снизить уровень беспорядка. Правильная сортировка данных — ключ к эффективной работе с массивами и быстрому доступу к нужной информации. Сравнение и перестановка элементов помогут вам добиться желаемого результата и оптимизировать структуру данных.

Статья основана на обсуждении Валерия в Twitter. В этом треде рассматриваются важные аспекты, связанные с текущими тенденциями и проблемами в определенной области. Основное внимание уделяется ключевым вопросам, которые волнуют общество, а также возможным решениям. Валерий делится своими мыслями и анализом, что позволяет читателям глубже понять ситуацию. Обсуждение в Twitter становится платформой для обмена мнениями и формирования общественного мнения. Эта статья служит дополнением к треду, предоставляя более детализированный обзор и анализ поднятых тем.

Сравнение элементов массива с соседними индексами является основным шагом в сортировке. Если значение элемента с индексом i больше значения элемента с индексом i + 1, то нужно поменять их местами. Данный подход позволяет постепенно упорядочить массив. Рассмотрим реализацию этого алгоритма в виде кода.

«`python
for i in range(len(array) — 1):
if array[i] > array[i + 1]:
array[i], array[i + 1] = array[i + 1], array[i]
«`

В этом коде происходит последовательное сравнение элементов массива и обмен их местами при необходимости. Такой метод можно использовать как часть более сложных алгоритмов сортировки, например, пузырьковой сортировки.

Этот код является отличной основой для реализации сортировки массива от наименьшего к наибольшему элементу. Однако его необходимо доработать для достижения оптимальной производительности и эффективности.

Сначала применим указанные команды ко всем элементам массива, за исключением последнего. Это необходимо, чтобы избежать выхода за границы массива и, как следствие, возникновения ошибки. Поэтому мы используем n — 1.

Данный код не предназначен для сортировки массива, однако он поможет упорядочить его элементы. Приведем пример его работы:

Обратите внимание: почти все элементы массива переместились в нужном направлении, а наибольший элемент (9) оказался в крайней правой ячейке. На каждой итерации он обменивался местами с соседом справа, благодаря чему «всплыл на поверхность». Этот процесс иллюстрирует принцип сортировки, где наибольший элемент постепенно поднимается к своему окончательному месту в отсортированном массиве.

Выполним наш код несколько дополнительных раз.

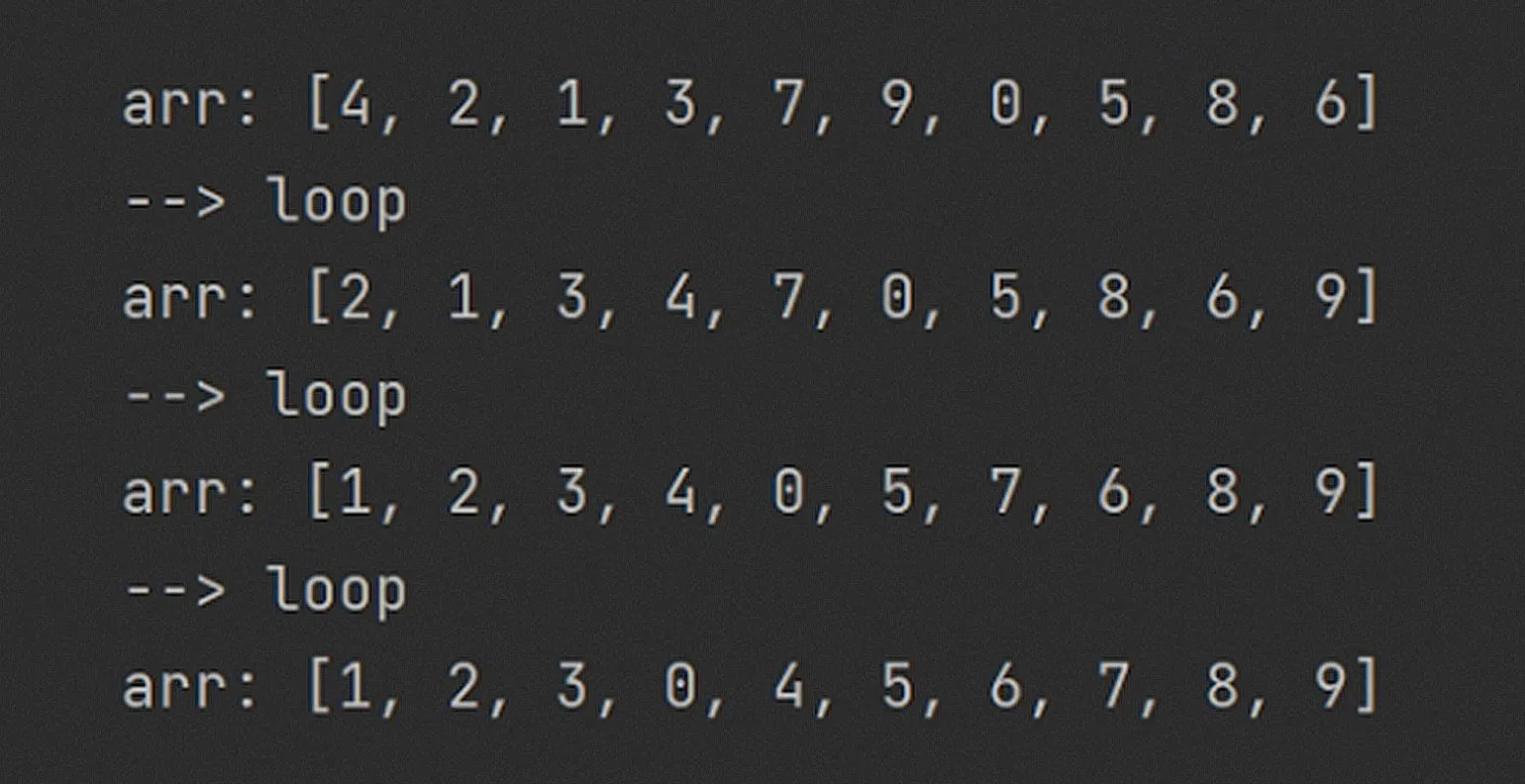
За три прохода данные значительно упорядочились. Каждый виток алгоритма обеспечивает правильное расположение одного из элементов: на первом шаге число 9 заняло своё место, на втором — число 8, а затем, благодаря удачному стечению обстоятельств, сразу четыре элемента были правильно размещены. Такой подход позволяет эффективно организовать данные и оптимизировать процесс сортировки.

Для гарантированной сортировки массива необходимо выполнить определенное количество перестановок. Если учитывать, что на каждом проходе алгоритм выталкивает минимум один элемент на его окончательную позицию, то для полной сортировки массива потребуется не менее n проходов. Однако можно обойтись и n — 1 проходами, поскольку на последнем проходе для крайнего правого элемента останется только один вариант размещения. Это делает алгоритм сортировки эффективным, особенно в случае, когда количество элементов в массиве велико.

Мы представляем вам первый алгоритм сортировки — пузырьковую сортировку, или Bubble Sort. Этот метод работает по принципу, при котором в каждой итерации более крупные элементы поднимаются на верх, а меньшие элементы опускаются вниз. Аналогия с пузырьками воздуха, всплывающими в воде, послужила основой для названия данного алгоритма. Пузырьковая сортировка является простым, но наглядным способом упорядочивания данных, что делает её популярной для обучения основам алгоритмов и структур данных.

Как работает Bubble Sort

Наша реализация алгоритма «пузырька» отличается простотой: в лучшем и худшем случае её временная сложность составляет O(n^2). Хотя этот подход является достаточно надёжным, существуют более эффективные алгоритмы сортировки, которые могут значительно улучшить производительность. Мы можем рассмотреть альтернативные методы, такие как сортировка слиянием или быстрая сортировка, которые обеспечивают более низкую временную сложность и оптимизированное использование ресурсов.

Каждое выполнение внутреннего цикла эффективно перемещает один правый элемент на его правильную позицию. Это позволяет с каждым новым значением j сокращать диапазон прохода внутреннего цикла на единицу. Таким образом, нет необходимости обрабатывать элементы, которые уже находятся на своих местах. Это оптимизирует процесс сортировки и повышает его эффективность.

В строке 3 необходимо добавить смещение j. Это позволит корректно настроить позиционирование элементов и улучшить читаемость кода. Важно учитывать, что правильно заданное смещение способствует оптимизации работы программы и повышению её эффективности. Убедитесь, что внесенные изменения соответствуют общей логике алгоритма и не вызывают ошибок в дальнейших вычислениях.

Программа улучшилась, но все еще выполняет много лишних операций. В одной итерации может сразу «всплыть» несколько элементов. Как обеспечить остановку программы, когда массив полностью отсортирован? Это можно сделать следующим образом:

Первым шагом необходимо добавить проверку на то, была ли произведена хотя бы одна перестановка за итерацию. Если перестановок не произошло, значит массив отсортирован, и программа может завершить свою работу. Это позволит значительно сократить количество итераций и повысить эффективность алгоритма сортировки.

Также можно использовать флаг, который будет указывать на необходимость продолжения сортировки. Если за текущую итерацию не будет изменений, программа завершит выполнение. Таким образом, вы сможете оптимизировать процесс сортировки и улучшить производительность вашей программы.

В нашей разработке была добавлена новая переменная, которая инициализируется значением false в начале внешнего цикла. После каждого обмена (свопа) эта переменная изменяет свое значение на true. Это позволяет эффективно отслеживать изменения в процессе выполнения алгоритма. Использование данной переменной способствует оптимизации работы кода и улучшению его производительности.

Если внутренний цикл не выполнит ни одного обмена (свопа), переменная сохранит значение false, что приведет к прерыванию внешнего цикла. Таким образом, в лучшем случае временная сложность алгоритма составляет O(n).

Если алгоритм работает с уже отсортированным массивом, достаточно одного прохода внутреннего цикла для выявления отсутствия перестановок, что позволяет прервать внешний цикл. Это решение напоминает метод сортировки пузырьком, который можно смело представить на собеседовании.

Обернем код в функцию и продолжим развивать нашу идею. Это позволит нам структурировать код, повысив его читаемость и повторное использование. Функции упрощают процесс разработки, так как обеспечивают модульность и легкость в отладке. Давайте сосредоточимся на создании эффективного и понятного кода, который будет легко адаптировать под новые задачи.

В таблице представлены значения временной сложности (Time Complexity) для различных сценариев: лучший, средний и худший случаи входных данных, а также значения пространственной сложности (Space Complexity). Эти показатели являются ключевыми для оценки эффективности алгоритмов и помогают разработчикам в выборе оптимальных решений для обработки данных. Правильное понимание временной и пространственной сложности позволяет улучшить производительность приложений и оптимизировать использование ресурсов.

Как работает Selection Sort

Пузырьковая сортировка основывается на сравнении соседних элементов массива. Однако существуют и другие методы сортировки массивов. Рассмотрим несколько альтернативных подходов. Например, быстрая сортировка, которая разделяет массив на подмассивы и сортирует их рекурсивно. Ещё одним популярным методом является сортировка слиянием, где массив делится на две половины, каждая из которых сортируется отдельно, а затем объединяется в отсортированный массив. Существуют и другие алгоритмы, такие как сортировка вставками и выбором, каждый из которых имеет свои преимущества и недостатки. Выбор метода сортировки зависит от конкретных условий, таких как размер массива и его предварительное состояние.

На столе перед мальчиком (или девочкой) разбросаны карточки с числами. Задача состоит в том, чтобы упорядочить эти числа по возрастанию. Сначала он ищет карточку с самым маленьким числом и откладывает её на соседний стол. После этого он возвращается к перемешанным карточкам и находит следующее наименьшее число. Забрав эту карточку, он помещает её на второй стол, расположенный справа от первой. Такой метод позволяет эффективно организовать числа в порядке возрастания.

Мальчик шаг за шагом создаст последовательность чисел. Легко догадаться, что этот массив будет отсортирован по возрастанию: наименьшее число окажется слева, а наибольшее — справа. Это принцип работы наивной сортировки выбором, известной как Selection Sort. Рассмотрим, как можно реализовать этот алгоритм в виде кода.

Для эффективного поиска индекса наименьшего элемента в массиве мы можем использовать специализированную функцию. Эта функция будет перебором элементов массива определять, какой из них имеет наименьшее значение, и возвращать соответствующий индекс. Такой подход позволяет оптимально обрабатывать данные и упрощает дальнейшие манипуляции с массивом. Важно учитывать, что при реализации этой функции следует учитывать возможные ошибки, такие как пустые массивы. Правильная обработка этих случаев обеспечит стабильность работы алгоритма и его корректность в различных сценариях.

Можно было бы обойтись без переменной current_min_value, но я предпочитаю оставить её для лучшего понимания кода. Эта переменная помогает наглядно отследить минимальное значение, что может быть полезно при дальнейшем анализе данных или отладке.

Функция find_min() имеет простое предназначение: она находит минимальное значение в массиве. Начнем с того, что первым элементом массива будем считать текущий минимум. Затем последовательно сравниваем этот элемент с остальными. Если встречается значение, которое меньше текущего минимума, мы обновляем значение переменной current_min_value. Таким образом, функция позволяет эффективно определить наименьший элемент массива, используя простой алгоритм сравнения.

Предполагаем, что массив arr содержит минимум один элемент и все его ячейки заполнены числовыми значениями. В противном случае функция find_min() может оказаться еще более сложной и трудной для понимания.

Для реализации функции, которая удаляет элемент из массива, можно воспользоваться простым подходом. Эта функция будет принимать два параметра: исходный массив и элемент, который необходимо удалить. В результате работы функции будет возвращен новый массив, в котором исключен указанный элемент. Такой метод позволяет сохранить оригинальный массив неизменным и улучшить читаемость кода. Пример реализации может выглядеть следующим образом:

«`javascript
function removeElement(arr, element) {
return arr.filter(item => item !== element);
}
«`

Данная функция использует метод `filter`, который создает новый массив, включающий только те элементы, которые не равны переданному значению. Таким образом, мы получаем чистый и понятный код, который эффективно выполняет задачу удаления элемента из массива.

Приготовления завершены, и теперь мы готовы к сортировке. Будем постепенно уменьшать оригинальный массив, формируя результат в новом массиве. Для начала создадим пустой массив с тем же размером, что и у исходного.

В следующем этапе мы осуществим реализацию шагов нашего мысленного эксперимента в виде программного кода. Это позволит нам наглядно увидеть, как теоретические концепции могут быть применены на практике. Программный код будет отражать основные принципы, которые мы обсудили, и продемонстрирует их функциональность. Таким образом, мы сможем анализировать результаты и делать выводы, основываясь на полученных данных. Подход к написанию кода будет систематичным и последовательным, что обеспечит его понятность и удобство в дальнейшем использовании.

К алгоритму могут возникнуть следующие замечания:

1. Эффективность: алгоритм может проявлять низкую производительность при обработке больших объемов данных, что может негативно сказаться на скорости выполнения задач.

2. Комплексность: сложность алгоритма может затруднять его понимание и внедрение, особенно для пользователей с ограниченными знаниями в этой области.

3. Гибкость: алгоритм может не учитывать все возможные сценарии или варианты использования, что ограничивает его применение в различных условиях.

4. Масштабируемость: при увеличении нагрузки алгоритм может не адаптироваться к новым условиям, что делает его менее надежным в долгосрочной перспективе.

5. Точность: возможны ошибки в вычислениях или некорректные результаты, что может привести к неправильным выводам и решениям.

Эти замечания требуют внимательного анализа и доработки алгоритма для повышения его эффективности и надежности.

• Он ест слишком много памяти. Мы создаём отдельный массив под результат и получаем O(n) по памяти.
• В оригинальном массиве появляются дыры. Функция delete_element() создаёт пустые ячейки в arr, о которые споткнётся find_min().
• Высокая Time Complexity. Алгоритм явно не блещет скоростью исполнения — O(n^2) как в худшем, так и в лучшем случае.

Возникает естественный вопрос: что делать в данной ситуации? В начале может показаться запутанным, но уверяю вас, вскоре всё станет ясно и логично.

Вот оптимизированный код для алгоритма сортировки выбором (Selection Sort). Этот алгоритм сортирует элементы непосредственно в исходном массиве arr, без создания дополнительного массива. Selection Sort является простым, но эффективным способом упорядочивания данных в небольших коллекциях. Его основное преимущество заключается в том, что он работает с минимальным объемом памяти, так как не требует дополнительных структур для хранения отсортированных данных.

«`python
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
return arr
«`

Данный код реализует сортировку выбором, находя минимальный элемент в неотсортированной части массива и перемещая его в начало. Это позволяет эффективно отсортировать массив с минимальным использованием памяти, что делает алгоритм подходящим для работы с небольшими объемами данных.

Я разработал функцию find_min_between(array, start_idx, end_idx), которая выполняет ту же задачу, что и функция find_min(array), но ограничивается определенным диапазоном индексов от start_idx до end_idx. Это позволяет более эффективно находить минимальное значение в заданном участке массива. Функция swap(array, i, j) также остается неизменной и не требует дополнительных пояснений.

Теперь рассмотрим, как функционирует усовершенствованная версия сортировки выбором. Начнем с массива arr, содержащего десять чисел. Улучшенная сортировка выбором оптимизирует процесс, уменьшая количество обменов элементов и повышая общую эффективность сортировки. Вместо того чтобы выполнять обмены на каждом шаге, алгоритм сначала находит минимальный элемент в оставшейся части массива, а затем производит один обмен для перемещения этого элемента на правильное место. Это позволяет сократить количество операций, особенно при работе с большими массивами. Применение усовершенствованной сортировки выбором может значительно улучшить производительность в сравнении с классическим методом, особенно в задачах, где важна скорость обработки данных.

В данном примере мы несколько раз пройдём по массиву, используя алгоритм сортировки выбором (selection sort), и проанализируем состояние массива arr на каждом этапе. Результаты выполнения алгоритма позволят нам увидеть, как происходит сортировка и как изменяется порядок элементов в массиве.

Алгоритм поддерживает порядок элементов в левой части массива arr, используя барьер между отсортированной и неотсортированной частью. Этот барьер располагается между элементами с индексами i и (i + 1). С помощью этого подхода обеспечивается эффективное распределение данных и поддержание их порядка, что способствует оптимизации сортировки и повышению производительности алгоритма.

В каждой итерации алгоритм находит минимальное значение в правой части массива, начиная с индекса i + 1 и до его конца, и меняет это значение местами с элементом, находящимся по индексу i. Таким образом, при i = 1 в отсортированной части массива находится только один элемент, а при i = 2 — уже два элемента. Этот подход обеспечивает последовательное упорядочение элементов массива, что делает алгоритм эффективным для сортировки данных.

Улучшение наглядности процесса сортировки можно достичь добавлением визуального разделителя между элементами массива, которые находятся по одну сторону от отсортированной части и по другую сторону от неотсортированной части. Такой подход поможет лучше понять, как происходит сортировка и какие элементы уже упорядочены, а какие еще требуют обработки. Это визуальное представление позволит легче следить за процессом и быстрее усвоить алгоритмы сортировки.

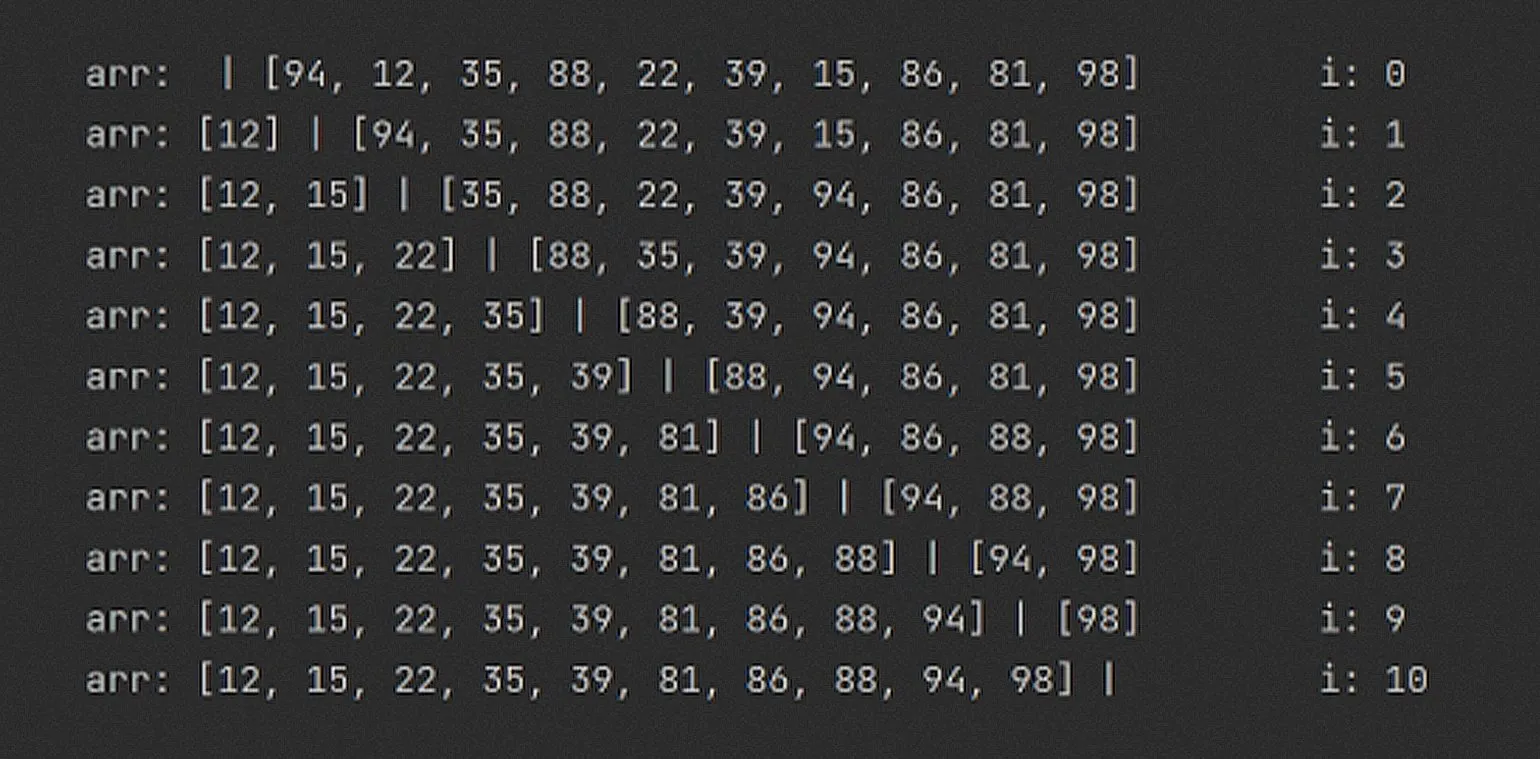
Имейте в виду, что состояние массива arr отображается по завершении каждой итерации. Первая строка соответствует i = 0, вторая строка — i = 1 и так далее.

Идея алгоритма Selection Sort становится понятной и логичной. Рассмотрим его основные характеристики. Алгоритм сортировки выбором последовательно находит минимальный элемент в неотсортированной части массива и перемещает его в начало. Это позволяет эффективно организовать сортировку данных. Selection Sort имеет временную сложность O(n²), что делает его менее эффективным для больших массивов. Тем не менее, его простота и наглядность делают его хорошим выбором для образовательных целей и небольших объемов данных. Теперь давайте более подробно обсудим его особенности и применение.

Данная реализация имеет преимущества в плане использования памяти, достигая сложности O(1) благодаря работе с левой частью массива. Однако поиск минимального элемента требует O(n) времени и выполняется в каждом цикле, что приводит к общему времени выполнения в O(n^2) как в худшем, так и в лучшем случае. Это делает данную реализацию неэффективной для больших массивов, так как время выполнения существенно увеличивается. Оптимизация алгоритма может значительно улучшить его производительность и сделать его более подходящим для работы с большими объемами данных.

На первый взгляд, может показаться, что алгоритм сортировки пузырьком (Bubble Sort) быстрее, чем алгоритм сортировки выбором (Selection Sort), благодаря своей лучшей временной сложности в лучшем случае O(n). Однако, как в известном анекдоте, здесь есть свои нюансы. В данной статье мы также рассмотрим аспекты, которые не охватывает О-нотация, и разберем, почему важно учитывать не только теоретическую сложность, но и практическое время выполнения этих алгоритмов в различных ситуациях.

Мы обновим таблицу с характеристиками, добавив новые данные и уточнения. Это поможет лучше понять особенности продукта и повысит его привлекательность для потенциальных покупателей. Обновленная таблица будет содержать актуальную информацию о характеристиках, что улучшит SEO-оптимизацию и повысит видимость страницы в поисковых системах.

Как работает Insertion Sort

Сортировка вставками, известная как Insertion Sort, имеет много общего с сортировкой выбором (Selection Sort). По сути, её можно назвать «обратной сортировкой выбором», так как она использует противоположный подход к организации данных. В отличие от сортировки выбором, которая ищет наименьший элемент и ставит его в начало, сортировка вставками постепенно строит отсортированный массив, включая элементы один за другим. Этот алгоритм эффективен для небольших наборов данных и позволяет добиться хороших результатов при частично отсортированных коллекциях. Сортировка вставками является простым и интуитивно понятным методом, что делает её популярным выбором для обучения основам алгоритмов сортировки.

В алгоритме сортировки выбором (Selection Sort) мы находим наименьший элемент в правой части массива и перемещаем его в конец левой части. Процесс продолжается до тех пор, пока не будет отсортирован весь массив. Самая затратная операция в этом алгоритме заключается в поиске наименьшего элемента, что может повлиять на общую производительность. Эффективность алгоритма сортировки выбором снижается при работе с большими объемами данных из-за его временной сложности, равной O(n^2), что делает его менее предпочтительным по сравнению с другими алгоритмами сортировки, такими как Quick Sort или Merge Sort. Тем не менее, Selection Sort прост в реализации и может быть полезен для небольших массивов или в образовательных целях для понимания основ сортировки.

Insertion Sort сохраняет упорядоченные элементы в исходном массиве. В этом алгоритме мы берем первый элемент из неупорядоченной правой части и вставляем его на правильную позицию в упорядоченной левой части. Этот процесс повторяется до тех пор, пока весь массив не будет отсортирован. Алгоритм эффективен для небольших объемов данных и работает с временной сложностью O(n^2) в худшем случае.

Левая часть массива всегда остается отсортированной. Это означает, что для добавления нового элемента нам нужно всего лишь найти правильную позицию для вставки. После этого необходимо сдвинуть все элементы справа на одну позицию вправо и поместить новый элемент на освободившееся место. Такой подход обеспечивает эффективное обновление массива без необходимости полной переработки его структуры.

Алгоритм сортировки вставками (Insertion Sort) можно сравнить с толкучкой в общественном транспорте. Когда тяжеловесный боксер входит в переполненный трамвай, его появление вызывает движение всех пассажиров, сдвигая их на полшага от выхода. Так же и в алгоритме сортировки вставками, элементы массива поочередно сравниваются и перемещаются, чтобы упорядочить последовательность. Этот метод эффективно работает на небольших объемах данных и демонстрирует свою эффективность при частично отсортированных массивах, что делает его полезным в определённых ситуациях.

Рассмотрим пример вставки числа в отсортированный массив. У нас есть отсортированный массив из восьми чисел с пустой ячейкой в конце. Задача состоит в том, чтобы вставить число 5 на корректную позицию, сохраняя порядок сортировки. Алгоритм вставки будет следующим: сначала необходимо пройти по элементам массива, сравнивая их с числом 5. Когда будет найден элемент, который больше 5, мы переместим все последующие элементы на одну позицию вправо и вставим 5 в найденное место. Таким образом, массив останется отсортированным.

Начнем перемещать числа больше 5 вправо. Это действие может быть полезным для упрощения анализа данных, визуализации или упорядочивания информации. Перемещение чисел в боковые позиции позволяет выделить их и облегчить восприятие. Такой подход часто используется в различных контекстах, включая обработку массивов и структур данных. Продолжая, мы можем рассмотреть, как подобные методы влияют на эффективность работы с информацией и повышают удобство использования.

При перемещении числа справа появляется его копия, в то время как оригинал заменяется соседним значением слева на следующем этапе.

После выполнения всех сдвигов массив будет выглядеть следующим образом:

Когда цикл достигнет значения 4, он завершит выполнение и заменит «мусорное» число 6 на 5.

Теперь рассмотрим алгоритм сортировки вставками (Insertion Sort). Этот метод является простым, но эффективным для сортировки небольших массивов. Суть алгоритма заключается в том, что он проходит по массиву, постепенно наращивая отсортированную часть. Каждый элемент вставляется в правильную позицию среди уже отсортированных данных. Сортировка вставками хорошо подходит для почти отсортированных массивов и демонстрирует хорошую производительность в таких случаях. Основное преимущество этого алгоритма — его простота и легкость в реализации, что делает его идеальным для обучающих целей и небольших задач сортировки. В следующем разделе мы рассмотрим реализацию кода для алгоритма сортировки вставками, чтобы понять его работу на практике.

Вспомните о барьере, который использовался в алгоритме Selection Sort. Поскольку алгоритм Insertion Sort имеет схожие принципы работы, давайте применим аналогичный прием и для него. Insertion Sort, как и Selection Sort, предназначен для сортировки массивов, но работает по другому принципу. Вместо поиска минимального элемента, этот алгоритм последовательно перемещает элементы и вставляет их в правильные позиции. Используя барьер, можно оптимизировать процесс, что повысит эффективность сортировки. Применение такого подхода поможет улучшить производительность Insertion Sort в определенных сценариях, особенно при работе с частично отсортированными массивами.

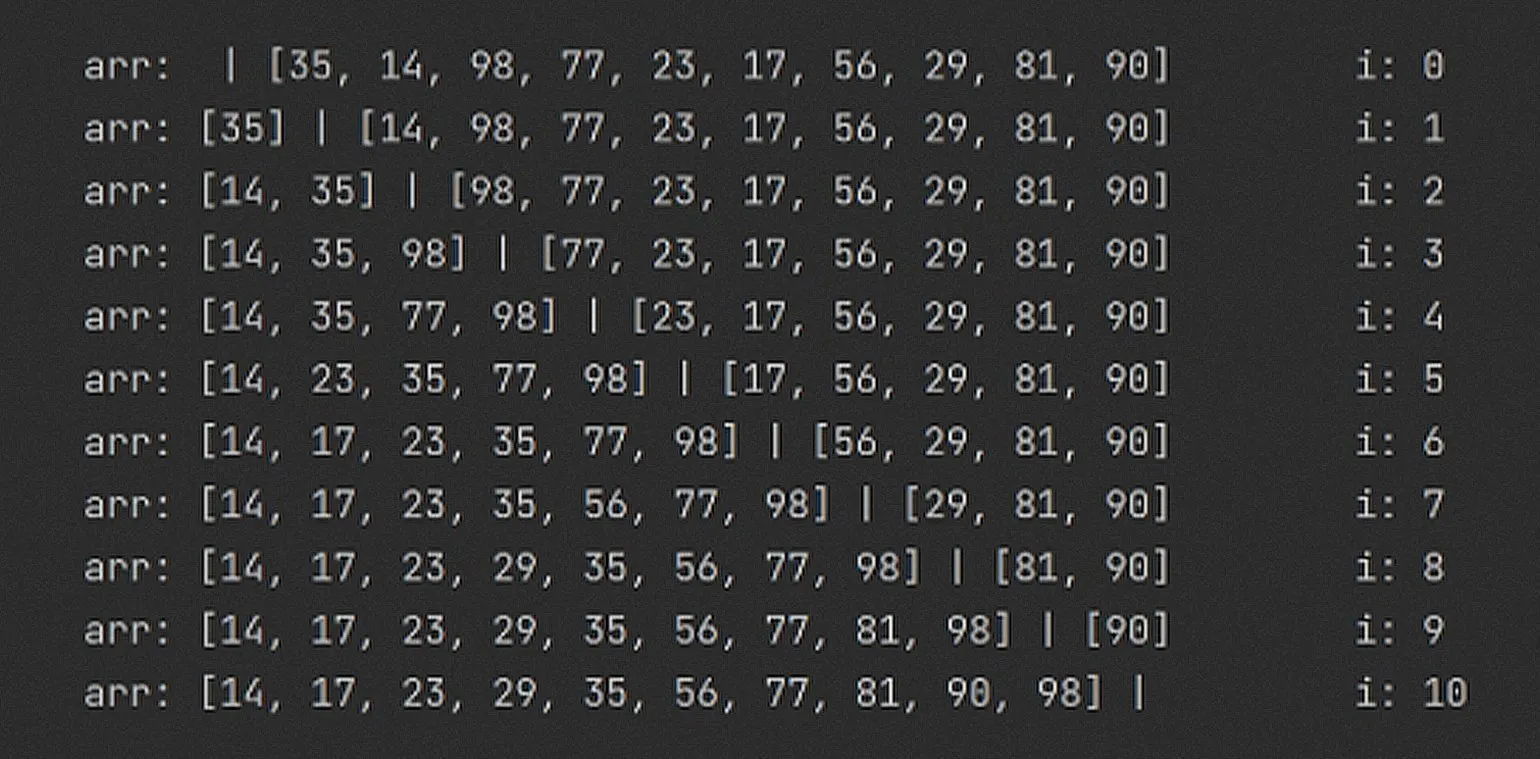
Нижняя граница производительности сортировки имеет важное значение. В случае, если массив уже отсортирован, не требуется производить никаких сдвигов. В этом случае сложность в лучшем случае составляет O(n), что делает данную сортировку особенно эффективной для отсортированных данных. Оптимизация алгоритмов сортировки позволяет значительно повысить производительность при работе с большими массивами, что имеет практическое значение в различных областях, включая обработку данных и алгоритмическое программирование.

Мы рассмотрели «Великую Тройку Сортировок», с которой сталкивается каждый, кто изучает алгоритмы. Поздравляю всех с этим важным шагом в понимании основ алгоритмической сортировки. Эти алгоритмы являются ключевыми инструментами в программировании и способствуют оптимизации работы с данными.

Что такое стабильность сортировки

Стабильный алгоритм сортировки, также известный как устойчивый, сохраняет порядок элементов с одинаковыми ключами относительно друг друга. Это означает, что при сортировке объектов с одинаковыми значениями атрибутов их первоначальная последовательность будет сохранена. В случае сортировки чисел стабильность не имеет большого значения, однако при работе с объектами, где важен исходный порядок, стабильные алгоритмы сортировки становятся критически важными. С помощью устойчивых алгоритмов можно избежать потери информации и сохранить контекст данных.

Для сортировки массива записей о клиентах по возрасту можно использовать простой формат записи в виде [возраст : имя]. Этот подход позволяет эффективно организовать данные и быстро находить нужные записи. Сортировка по возрасту позволяет упорядочить клиентов, что может быть полезно для анализа и принятия решений в бизнесе. Важно учитывать, что правильная сортировка данных помогает лучше понимать аудиторию и оптимизировать взаимодействие с клиентами. Используя данный формат, вы сможете легко обрабатывать и анализировать информацию о возрасте клиентов, что в свою очередь улучшит качество обслуживания и повысит эффективность маркетинговых стратегий.

После выполнения стабильной сортировки элемент Кузи окажется выше элемента Олега. Это связано с тем, что в стабильной сортировке сохраняется порядок элементов с одинаковыми ключами, как это было в исходных данных. Таким образом, при сортировке Кузя будет гарантированно находиться перед Олегом.

В условиях нестабильности возможен второй сценарий.

Стабильность является ключевым фактором при сортировке массивов объектов по нескольким критериям. Например, если мы сортируем данные сначала по возрасту, затем по размеру банковского счёта и, наконец, по площади жилья, нестабильный алгоритм может привести к неочевидным результатам. В таких случаях важно использовать стабильные алгоритмы сортировки, чтобы гарантировать, что объекты с одинаковыми значениями по первому критерию сохраняли порядок, в котором они были изначально. Это особенно актуально в приложениях, где точность и предсказуемость данных играют критическую роль. Выбор стабильного алгоритма сортировки поможет избежать путаницы и обеспечит более точный и логичный вывод.

В нашей группе алгоритмов сортировки два метода, Bubble Sort и Insertion Sort, демонстрируют стабильность в работе, тогда как Selection Sort склонен к перемешиванию элементов. Стабильные алгоритмы сортировки сохраняют порядок равных значений, что делает их предпочтительными в определенных задачах. Bubble Sort и Insertion Sort обеспечивают такую стабильность, что может быть критически важно при обработке данных. В то же время, Selection Sort не гарантирует сохранение порядка, что ограничивает его использование в некоторых сценариях.

Добавим в нашу таблицу характеристики алгоритма Selection Sort, включая информацию о стабильности. Это позволит более полно оценить его эффективность и применимость в различных сценариях.

Что не учитывает O(n)

Я обещал рассмотреть аспекты, которые O-нотация не учитывает. Теперь настало время проанализировать недостатки и особенности популярных алгоритмов.

Рассмотрим массив, который почти идеально отсортирован. Почти — потому что на первом месте находится самый большой элемент.

Алгоритмы, применяемые в различных сферах, будут адаптироваться к изменяющимся условиям и требованиям. Они способны анализировать и обрабатывать большие объемы данных, принимая во внимание множество факторов, таких как поведение пользователей, рыночные тренды и технологические новшества. Ожидается, что в ближайшем будущем алгоритмы станут еще более эффективными, улучшая качество предоставляемых услуг и повышая уровень персонализации. Они будут учитывать не только привычки пользователей, но и их предпочтения, что приведет к созданию более интуитивно понятных интерфейсов и решений. Кроме того, важной тенденцией станет акцент на прозрачность алгоритмов, что поможет пользователям лучше понимать, как принимаются решения и на каких данных они основываются. Таким образом, алгоритмы будут не только инструментом для анализа данных, но и важным элементом взаимодействия с пользователями, способствуя улучшению общего пользовательского опыта.

• Bubble Sort сработает великолепно. За n перестановок наибольший элемент «всплывёт» наверх.
• Insertion Sort тоже хорош в этом вопросе.
• Selection Sort со страшной расточительностью перелопатит весь массив и выдаст O(n^2) по времени.

Если данные почти отсортированы, то алгоритмы сортировки, такие как Bubble Sort и Insertion Sort, становятся наиболее эффективными инструментами. Эти методы демонстрируют отличные результаты при работе с почти упорядоченными массивами, обеспечивая быструю сортировку с минимальными затратами ресурсов. Выбор между ними зависит от конкретных условий и требований задачи, однако оба алгоритма способны значительно ускорить процесс обработки данных в таких случаях.

Теперь рассмотрим стоимость операций. Хотя в О-нотации этот аспект не обсуждается, важно понимать, что различные операции требуют различного объема ресурсов компьютера. Эффективность выполнения операций может значительно варьироваться в зависимости от сложности алгоритма и объема обрабатываемых данных. Понимание этих нюансов помогает разработчикам оптимизировать код и выбирать наиболее эффективные решения для конкретных задач.

Чтение значения из ячейки массива является простой задачей. Однако перезапись ячейки может показаться легкой, но на практике возникают сложности, связанные с многопоточностью, обновлением значений в кэше процессора и другими факторами реального мира. Таким образом, операция swap() оказывается более сложной, чем можно было бы предположить на первый взгляд.

В данном разделе мы рассмотрим количество свопов, которые были проведены. Это важный показатель, который позволяет оценить активность на платформе и уровень интереса пользователей к различным активам. Анализируя данные о свопах, можно выявить тенденции и предпочтения, что поможет в дальнейшей оптимизации предложений на рынке. Убедитесь, что вы в курсе последних изменений и обновлений в сфере свопов, чтобы принимать обоснованные решения.

• Bubble Sort просто монстр, который свопает без остановки. Количество операций записи здесь зашкаливает.
• Insertion Sort тоже не подарок — постоянное сдвигание элементов вправо до добра не доведёт.
• Selection Sort — конфетка! Всего n свопов в худшем случае. Очень экономичный алгоритм.

Если вашей целью является оптимизация затрат на операции записи, то алгоритм сортировки выбором (Selection Sort) станет наиболее подходящим вариантом. Этот алгоритм эффективен в контексте снижения количества записей, что делает его идеальным для использования в средах с ограниченными ресурсами или при необходимости минимизировать износ памяти.

Все три алгоритма демонстрируют одинаковую эффективность в использовании памяти. Они функционируют in-place, что позволяет им использовать O(1) памяти.

Алгоритмы сортировки всегда поддаются улучшению, особенно при использовании специализированных структур данных. Например, алгоритм Insertion Sort можно оптимизировать, увеличив его скорость в два раза и сократив количество операций свопа до уровня, сопоставимого с Bubble Sort, если вместо массива использовать связный список. Кроме того, алгоритм Selection Sort можно модифицировать, чтобы он работал как стабильный. Это открывает новые возможности для повышения эффективности сортировки данных и расширяет применимость различных алгоритмов в зависимости от конкретных задач.

Что почитать и посмотреть

На сайте geeksforgeeks.org вы можете найти код сортировок, реализованный на различных языках программирования, а также видеоматериалы, демонстрирующие визуализацию этих алгоритмов. Ресурс предлагает обширный выбор примеров, что позволяет лучше понять принципы работы сортировок и их применение в реальных задачах.

• Bubble Sort
• Selection Sort
• Insertion Sort

На YouTube представлено множество визуализаций алгоритмов сортировки, однако я хотел бы обратить ваше внимание на одно видео, которое выделяется среди остальных. В данном видео подробно демонстрируются различные алгоритмы сортировки, их принципы работы и эффективность. Это отличный ресурс для тех, кто хочет глубже понять, как различные алгоритмы могут влиять на обработку данных. Сравнение визуальных представлений помогает лучше усвоить материал и выбрать оптимальный подход к решению задач, связанных с сортировкой.

Венгерские танцы представляют собой уникальное культурное явление, которое сочетает в себе элементы традиции и развлечения. Эти танцы не только увлекательны, но и познавательны, позволяя глубже понять венгерскую культуру и ее музыкальные особенности. Их энергичные движения и яркие костюмы привлекают внимание и создают атмосферу веселья. Венгерские танцы стали популярными не только в самой Венгрии, но и за ее пределами, завоевывая сердца людей по всему миру.

На этом этапе мы завершили обсуждение простых сортировок. Надеюсь, информация была представлена ясно и доступно. В будущих статьях, посвящённых алгоритмам сортировки, я подробнее рассмотрю такие методы, как Merge Sort и Quick Sort, углубляясь в их особенности и применение.

Чтение является важным аспектом личностного роста и развития. Оно способствует расширению кругозора, улучшению словарного запаса и развитию критического мышления. Регулярное чтение не только обогащает знания, но и помогает справляться со стрессом, улучшая общее самочувствие. Выбирайте разнообразные жанры и тематики, чтобы сделать процесс чтения более увлекательным и полезным. Исследуйте новые авторов и книги, и не забывайте делиться своими впечатлениями с другими. Чтение — это ключ к новым возможностям и глубокому пониманию окружающего мира.

• Big O Notation: что это такое и как её посчитать
• GNU Emacs: как текстовый редактор из 1980-х учит программистов ценить свободное ПО
• Экспекто Питонум: 15 заклинаний на змеином языке