Числа Фибоначчи: 5 фактов о популярности и применении

Содержание:

• Что такое числа Фибоначчи?
• Происхождение чисел Фибоначчи: Исторический контекст
• Связь чисел Фибоначчи и золотого сечения: гармония в природе и искусстве
• Применение чисел Фибоначчи в различных областях
• Значение чисел Фибоначчи в природе и науке

Что такое числа Фибоначчи?

Числа Фибоначчи образуют уникальную последовательность, где каждое последующее число является суммой двух предыдущих. Эта последовательность начинается с двух начальных значений: 0 и 1. Последовательность Фибоначчи имеет широкий спектр применений, включая математику, искусство и природу. Каждое число в этой последовательности можно выразить как F(n) = F(n-1) + F(n-2), где F(0) = 0 и F(1) = 1. Числа Фибоначчи также известны своей связью с золотым сечением, что делает их важными в изучении пропорций и симметрии.

Последовательность Фибоначчи представляет собой математическую последовательность, в которой каждое число является суммой двух предыдущих. Начинается она с нуля и единицы, а затем продолжается как 0, 1, 1, 2, 3, 5, 8, 13, 21 и так далее. Эта последовательность имеет широкое применение в различных областях, таких как природа, искусство и финансы, и часто используется для описания ростов и структур в живых организмах, а также в алгоритмах и программировании. Интересно, что числа Фибоначчи также связаны с золотым сечением, что делает их особенно важными в эстетике и дизайне.

Последовательность чисел, представленных здесь, является знаменитой последовательностью Фибоначчи. Она начинается с двух единиц, после чего каждое следующее число является суммой двух предыдущих. Эта последовательность имеет множество применений в математике, науке и искусстве. Например, она часто встречается в природе, таких как спирали раковин и расположение листьев на стебле. Числа Фибоначчи также используются в алгоритмах, финансовом анализе и компьютерной науке. Понимание этой последовательности может помочь в решении различных задач и в более глубоком восприятии закономерностей, присутствующих в окружающем мире.

Этот числовой ряд, хотя и теоретически может продолжаться бесконечно, в большинстве практических задач обычно ограничивается первыми десятью числами последовательности. Эти числа предоставляют достаточную информацию для анализа и решения задач, связанных с данной последовательностью. Поэтому для большинства приложений в математике и смежных дисциплинах достаточно рассматривать именно эти десять значений.

• 1. Первое — 0;
• 2. Второе — 1;
• 3. Третье — 1;
• 4. Четвёртое — 2;
• 5. Пятое — 3;
• 6. Шестое — 5;
• 7. Седьмое — 8;
• 8. Восьмое — 13;
• 9. Девятое — 21;
• 10. Десятое — 34.

Сложение чисел зачастую воспринимается как простая операция, но на самом деле это лишь начало увлекательного мира числовых последовательностей. Существуют различные последовательности, в которых каждое число является суммой трех или четырех предыдущих. Эти сложные математические конструкции находят широкое применение в науке и технике. Рассмотрим, каким образом такие последовательности используются в различных областях, от компьютерных алгоритмов до биологических исследований. Понимание этих концепций открывает новые горизонты для применения математики в реальной жизни.

Числа Фибоначчи имеют глубокие исторические корни и значительное влияние на различные сферы науки и искусства. Эти числа были впервые описаны итальянским математиком Леонардо Пизанским в XIII веке, который известен под именем Фибоначчи. Его работа, «Liber Abaci», познакомила Европу с арабской системой счисления и понятием чисел Фибоначчи, которые образуются по простому правилу: каждое последующее число является суммой двух предыдущих.

Числа Фибоначчи находят применение в математике, биологии, искусстве и даже финансовых рынках. В математике они используются для изучения последовательностей и пропорций. В биологии эти числа описывают множество природных явлений, таких как расположение листьев на стебле растений или количество лепестков у цветов. В искусстве и архитектуре числа Фибоначчи связаны с золотым сечением, которое используется для создания гармоничных и эстетически привлекательных композиций.

Кроме того, числовая последовательность Фибоначчи находит применение в современных технологиях, таких как алгоритмы и программирование. Это делает их важным предметом изучения как для математиков, так и для специалистов в других областях. Таким образом, числа Фибоначчи представляют собой не только математическую любопытность, но и мощный инструмент для анализа и понимания окружающего мира.

Происхождение чисел Фибоначчи: Исторический контекст

Числа Фибоначчи, ставшие основой для множества математических концепций, были впервые описаны итальянским математиком Леонардо Пизанским, более известным как Фибоначчи. В XII веке он глубоко изучал труды древнегреческих и индийских учёных, что привело его к множеству значительных открытий, включая преимущества десятичной системы по сравнению с римскими цифрами. Числа Фибоначчи представляют собой последовательность, в которой каждое последующее число является суммой двух предыдущих, и эта последовательность встречается в различных областях науки, искусства и природы. Исследования Фибоначчи оказали значительное влияние на математику и продолжают использоваться в современных вычислениях и алгоритмах.

Леонардо Пизанский, известный как Фибоначчи, систематизировал свои знания в значительном произведении «Книга абака». В этом труде он впервые представил последовательность чисел Фибоначчи, применив ее к задаче о размножении кроликов. Эта последовательность стала основополагающей в математике и нашла применение в различных областях, включая биологию, компьютерные науки и экономику. «Книга абака» не только популяризировала арабские цифры в Европе, но и положила начало новым математическим исследованиям.

В загоне находятся две пары кроликов — один самец и одна самка. Каждый месяц эта пара кроликов производит на свет новую пару. Вопрос: сколько пар кроликов окажется в загоне через год?

Для решения этой задачи необходимо учитывать, что каждая новая пара начинает размножаться с первого месяца после своего рождения. Следовательно, количество пар будет удваиваться каждый месяц. Если в начале года у нас 2 пары, то через 12 месяцев их количество значительно возрастет.

Таким образом, расчет основан на принципах популяционной динамики и фибоначчиевой последовательности, что позволяет предсказать, сколько пар кроликов будет в загоне через год.

На первый взгляд, задача о размножении кроликов может показаться простой. Однако следует учитывать, что на этот процесс влияют множество факторов, включая вероятность гибели или побега животных. Чтобы упростить задачу, Фибоначчи ввёл определённые условия, которые помогают лучше понять динамику популяции кроликов и её развитие. Эти условия позволяют провести более точный анализ и прогнозирование численности кроликов в зависимости от заданных параметров.

• кролики не могут умереть;
• они достигают половой зрелости за месяц;
• самки беременны ровно месяц;
• кролики всегда рождаются парами: самец и самка.

При соблюдении данных условий задача становится решаемой, и ответом на нее является последовательность Фибоначчи. Каждая взрослая пара кроликов производит новую пару через месяц после своего появления, а потомство начинает размножаться через месяц после своего рождения. Эта модель размножения позволяет проследить, как быстро увеличивается число кроликов, что иллюстрирует прирост популяции и закономерности в природе. Последовательность Фибоначчи находит применение не только в биологии, но и в математике, искусстве и архитектуре, что подчеркивает ее универсальность и важность в различных областях.

Чтобы глубже понять процесс размножения кроликов, представьте себе график, иллюстрирующий, как число пар кроликов возрастает с каждым месяцем. Эта визуализация поможет наглядно отследить динамику роста популяции, демонстрируя, как быстро кролики могут размножаться и увеличивать свое количество в условиях благоприятной среды.

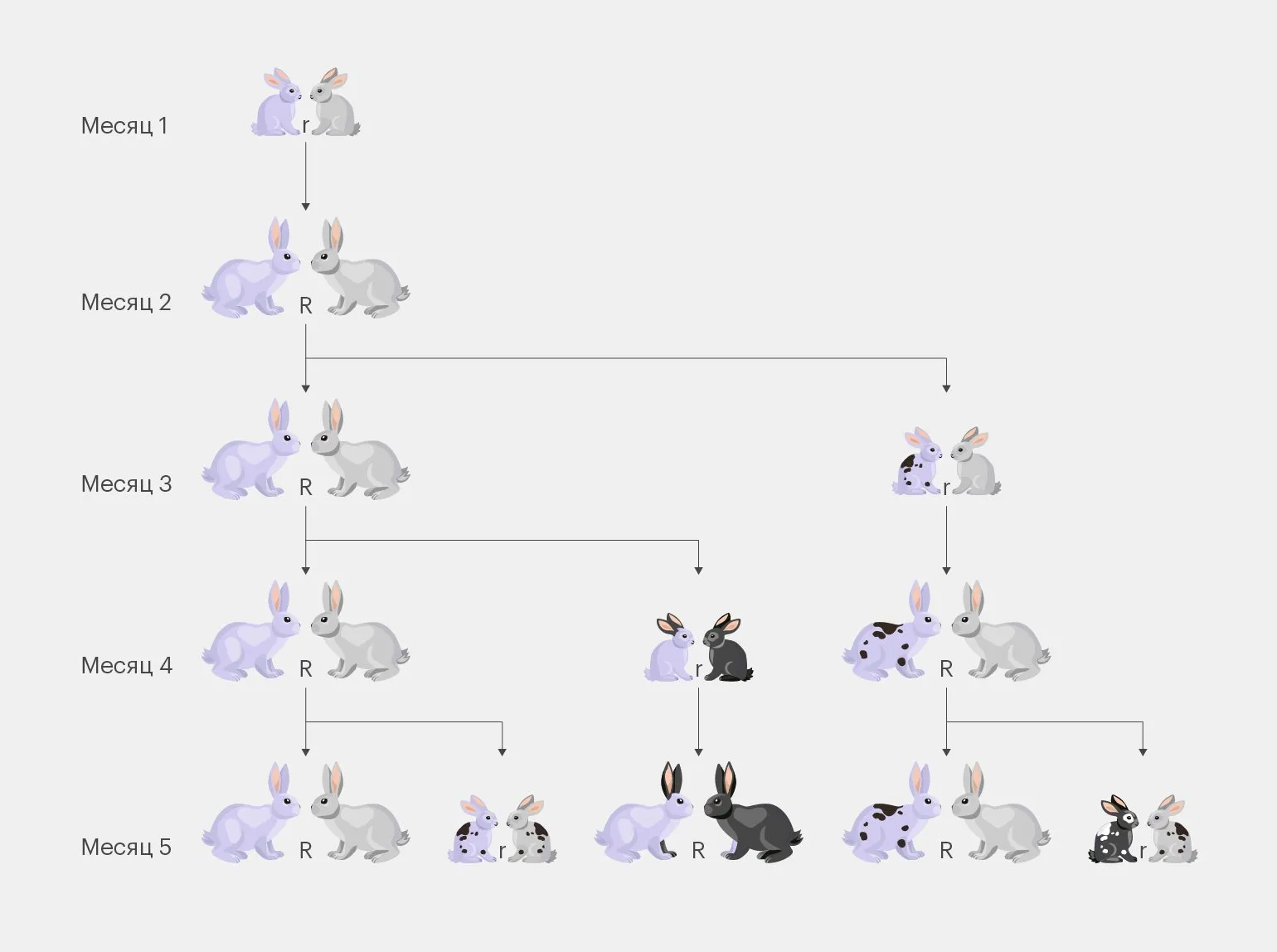
Сначала пара молодых кроликов не может размножаться. Однако через месяц они достигают половой зрелости, и на третий месяц в загоне появится уже две пары. В дальнейшем количество пар будет увеличиваться по принципу, при котором общее число пар в текущем месяце будет равно сумме пар за два предыдущих месяца. Эта последовательность напоминает известную числовую последовательность Фибоначчи. Таким образом, размножение кроликов демонстрирует экспоненциальный рост численности, что важно учитывать при планировании содержания и кормления животных.

Через год в загоне будет находиться 233 пары кроликов, что является решением данной задачи.

Числа Фибоначчи представляют собой не только математическую задачу о популяции кроликов. Леонардо Пизанский, известный как Фибоначчи, открыл путь к более сложным математическим концепциям. Последовательность Фибоначчи находит широкое применение в разных сферах, включая математику, архитектуру, искусство и биологию. Эти числа помогают описать естественные явления, такие как рост растений и пропорции в живой природе, а также используются в финансовом анализе и компьютерных науках. Их уникальные свойства и закономерности делают числа Фибоначчи важным инструментом для изучения и понимания различных процессов.

Связь чисел Фибоначчи и золотого сечения: гармония в природе и искусстве

Золотое сечение, обозначаемое как φ (фи), является математической константой, примерно равной 1,618. Это особое соотношение используется для деления объектов на части, которые воспринимаются как гармоничные и эстетически привлекательные. Например, если у вас есть два отрезка, более длинный отрезок должен быть в 1,618 раза длиннее короткого. В свою очередь, весь объект должен быть в 1,618 раза длиннее длинного отрезка. Золотое сечение находит применение в разных сферах, включая искусство, архитектуру и дизайн, благодаря своей способности создавать визуально привлекательные композиции.

Архитекторы античных и средневековых времен искали идеальные пропорции в своих произведениях. Золотое сечение служило основой для многих архитектурных шедевров, которые продолжают восхищать своей гармонией и красотой. Это математическое соотношение не только эстетически привлекательно, но и символизирует баланс и совершенство. Золотое сечение можно наблюдать в таких известных сооружениях, как Парфенон и соборы средневековой Европы. Эти элементы архитектуры продолжают вдохновлять современных дизайнеров и архитекторов, подчеркивая важность пропорций в создании визуально привлекательных пространств.

Золотое сечение на протяжении веков использовалось в архитектуре для создания визуального совершенства. Примеры таких сооружений, как Храм Парфенона в Афинах и Пирамида Хеопса в Гизе, наглядно иллюстрируют это. В Парфеноне гармония пропорций проявляется в соотношении колонн и фронтонов, что создает ощущение баланса и эстетической завершенности. Пирамида Хеопса также демонстрирует использование золотого сечения, обеспечивая идеальные пропорции, которые способствовали её величественному виду. Эти архитектурные достижения подчеркивают важность золотого сечения как инструмента для достижения гармонии и красоты в дизайне.

Числа Фибоначчи обладают удивительной связью с золотым сечением, также известным как «золотое отношение». При делении каждого элемента последовательности Фибоначчи, начиная с определённого номера, на его предшествующее значение, результат стремится к числу φ (примерно 1.6180339887). Эта связь становится особенно очевидной при анализе более высоких чисел в последовательности. Чем больше числа, тем ближе их соотношение к золотому сечению, что подчеркивает гармоничные пропорции, присутствующие как в математике, так и в природе. Знание этой уникальной связи может быть полезным для дизайнеров, архитекторов и художников, стремящихся использовать эстетические принципы в своих работах.

Если рассмотреть 31-е число Фибоначчи и разделить его на 30-е, результат окажется примерно равным 1,618. Хотя это значение не является точным, при дальнейшем движении по последовательности Фибоначчи соотношение стремится к золотому сечению. Это делает золотое сечение значимым как в математике, так и в природе. Золотое сечение встречается в различных аспектах, от архитектуры до живописи, и продолжает привлекать внимание ученых и художников благодаря своим эстетическим и математическим свойствам.

Золотое сечение широко используется не только в архитектуре, но и в таких сферах, как фотография, живопись и дизайн интерфейсов. Применение этих принципов в веб-дизайне позволяет создавать визуально привлекательные и гармоничные сайты. Разработка веб-сайтов с учетом золотого сечения помогает улучшить пользовательский опыт, привлекая внимание к важным элементам и создавая баланс между различными компонентами страницы. Использование золотого сечения в дизайне интерфейсов способствует более эффективной навигации и улучшению восприятия информации.

Числа Фибоначчи и золотое сечение имеют глубокую взаимосвязь и проявляются в природе. Эти математические принципы можно наблюдать в биологии, например, в распределении листьев на стебле растений и в спиральной структуре раковин моллюсков. Кроме того, они находят широкое применение в программировании и других современных науках, таких как архитектура и искусственный интеллект. Понимание этих концепций помогает не только в научных исследованиях, но и в практическом применении в различных областях, где важна гармония и эффективность.

Часто задаваемые вопросы о нашем продукте

Наши клиенты часто интересуются различными аспектами использования нашего продукта. В этом разделе мы собрали наиболее распространенные вопросы и предоставили на них исчерпывающие ответы. Если у вас есть дополнительные вопросы, не стесняйтесь обращаться к нашей службе поддержки.

Как работает наш продукт?
Наш продукт разработан с учетом потребностей пользователей и обеспечивает простоту в использовании. Он легко интегрируется в вашу повседневную практику и помогает оптимизировать рабочие процессы.

Какие преимущества использования нашего продукта?
Использование нашего продукта позволяет повысить эффективность работы, сократить время на выполнение задач и улучшить качество результатов. Мы стремимся предоставить вам инструменты, которые помогут достичь ваших целей.

Как связаться с поддержкой?
Наша служба поддержки доступна круглосуточно. Вы можете связаться с нами через форму обратной связи на сайте, по электронной почте или по телефону. Мы готовы помочь вам в любое время.

Каковы условия возврата товара?
Мы предлагаем политику возврата, которая позволяет вернуть продукт в течение 30 дней после покупки, если он не удовлетворяет вашим ожиданиям. Пожалуйста, ознакомьтесь с нашими условиями возврата на сайте для получения более детальной информации.

Надеемся, что эти ответы помогут вам лучше понять наш продукт и его возможности. Мы всегда готовы помочь вам и ответить на все ваши вопросы.

Золотое сечение играет важную роль в искусстве, поскольку оно способствует созданию гармоничных и визуально привлекательных произведений. Это математическое соотношение, равное примерно 1,618, помогает художникам и дизайнерам достигать эстетического равновесия и пропорций. Используя золотое сечение, мастера могут направлять взгляд зрителя, выделять ключевые элементы и обеспечивать эмоциональную целостность своих работ. Применение золотого сечения в живописи, архитектуре и других формах искусства подчеркивает его значимость как инструмента для достижения идеальной композиции и глубины восприятия.

Числа Фибоначчи можно наблюдать в различных аспектах природы. Эти последовательности проявляются в спиральной структуре раковин, расположении лепестков на цветках, а также в форме и структуре галактик. Изучение чисел Фибоначчи помогает понять природные закономерности и красоту, проявляющуюся в мире вокруг нас.

Числа Фибоначчи находят широкое применение в программировании, особенно в алгоритмах, связанных с оптимизацией и поиском. Они используются в различных областях, таких как динамическое программирование, анализ сложности алгоритмов и построение эффективных структур данных. Например, алгоритмы поиска, основанные на последовательности Фибоначчи, могут значительно улучшить производительность при работе с отсортированными массивами. Кроме того, числа Фибоначчи часто применяются в рекурсивных функциях, что позволяет эффективно решать задачи, такие как вычисление чисел Фибоначчи или нахождение наибольшего общего делителя. Использование чисел Фибоначчи в программировании открывает новые возможности для оптимизации процессов и повышения эффективности алгоритмов.

Применение чисел Фибоначчи в различных областях

Числа Фибоначчи представляют собой не только интересный математический феномен, но и имеют множество применений в различных областях, включая биологию, искусство и финансы. Эта последовательность не только отражает природные закономерности, но и является полезным инструментом для анализа финансовых рынков. Рассмотрим более подробно, как числа Фибоначчи влияют на нашу жизнь и какие возможности они открывают в различных сферах. Их использование в биологии помогает понять рост и развитие организмов, в искусстве — создать гармоничные композиции, а в финансах — прогнозировать движения цен на рынке. Таким образом, числа Фибоначчи играют важную роль в нашем понимании окружающего мира и помогают принимать обоснованные решения в разных областях.

Числа Фибоначчи можно увидеть в природе, особенно в растениях, таких как подсолнухи. При внимательном рассмотрении семян подсолнуха можно заметить, что они располагаются в виде спиралей: 21 спираль закручена по часовой стрелке, а 34 — против. Эти числа наглядно демонстрируют последовательность Фибоначчи, которая имеет важное значение в биологии и математике. Растения используют эту последовательность для оптимизации роста и распределения семян, что позволяет им эффективно использовать солнечный свет и питательные вещества.

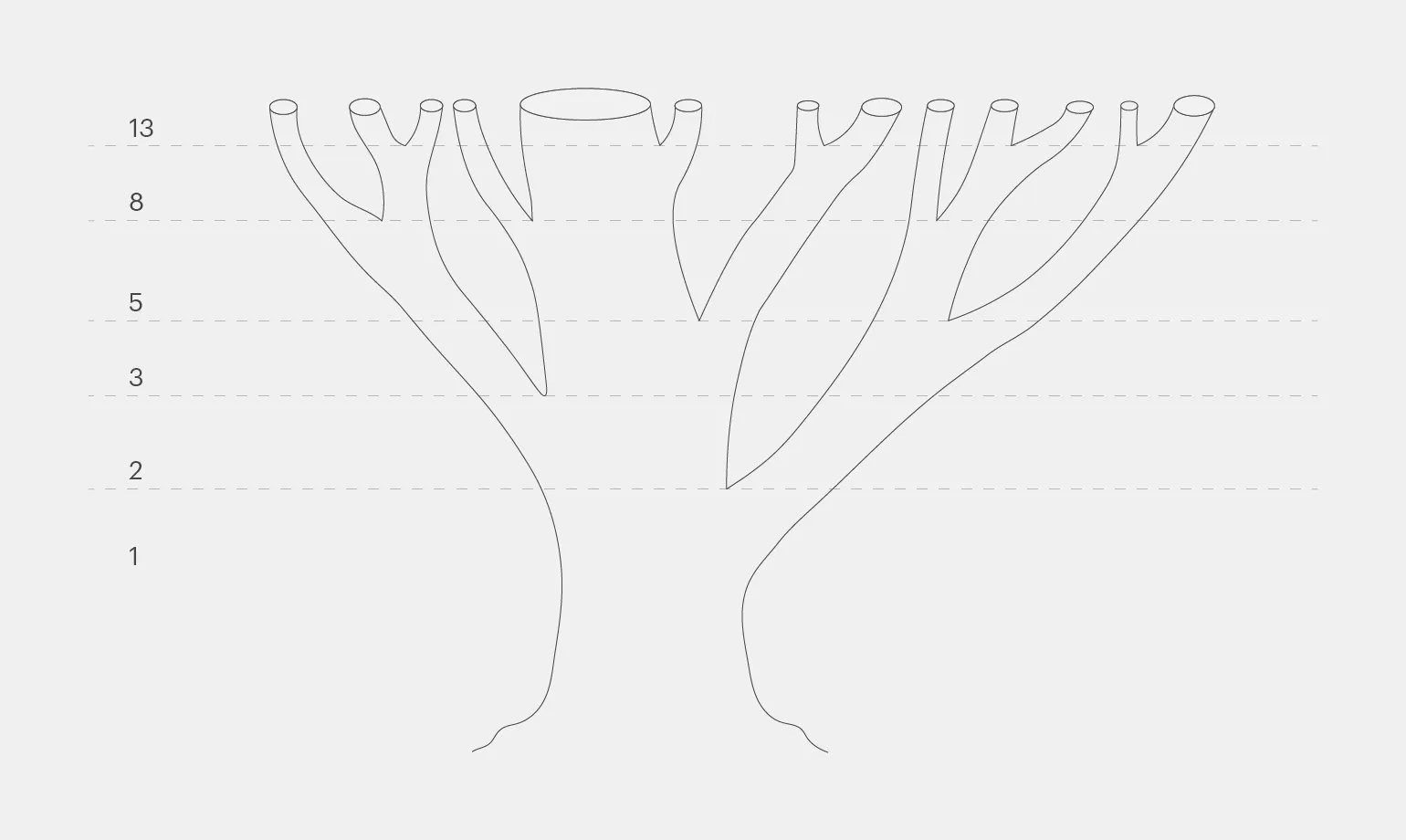
Числа Фибоначчи могут быть замечены в структуре деревьев, где каждая ветвь порождает новые ответвления, количество которых соответствует следующему числу в последовательности. Этот феномен иллюстрирует, как природа использует математику для создания гармонии и симметрии в своем развитии. Наблюдение за числами Фибоначчи в растительном мире подчеркивает связь между математическими концепциями и биологическими формами, что делает их важной темой для изучения в области ботаники и математической биологии.

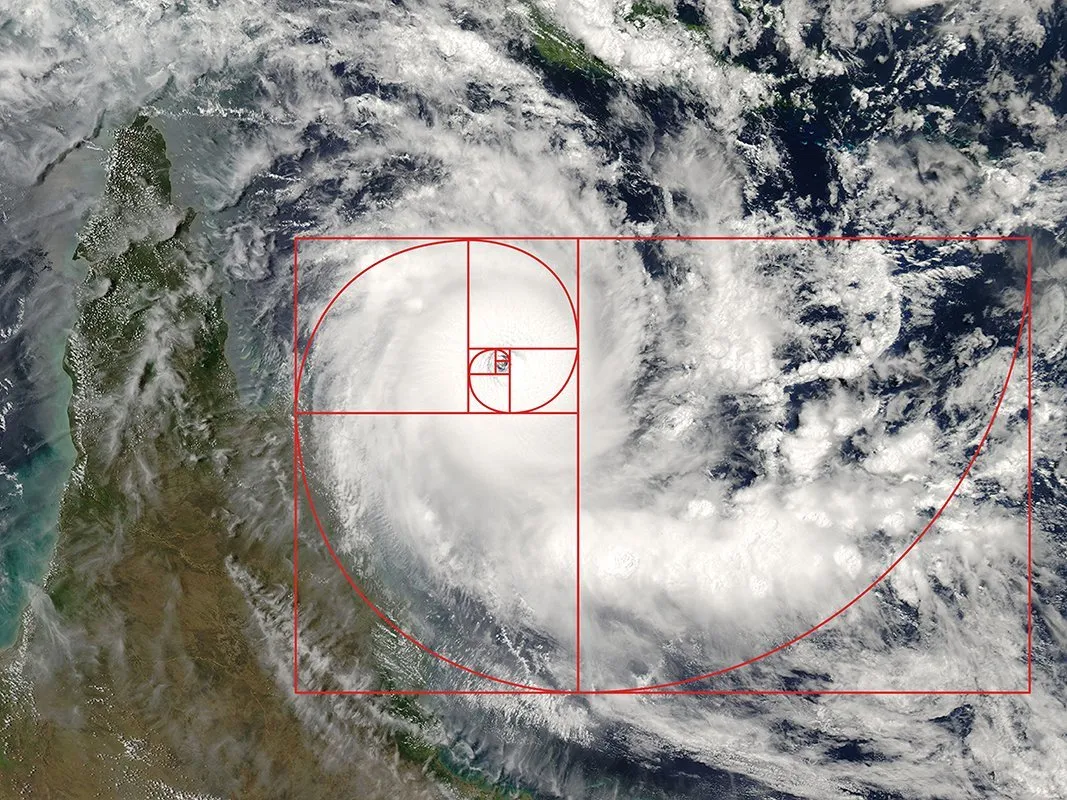
Золотое сечение, основанное на числах Фибоначчи, играет ключевую роль в образовании спиралей в природе, от улиток до галактик. Это удивительное явление вызывает глубокие размышления о структуре и организации нашей вселенной. Изучение золотого сечения и чисел Фибоначчи помогает понять, как гармония и пропорции проявляются в биологических формах и астрономических объектах, подчеркивая связь между математикой и природой.

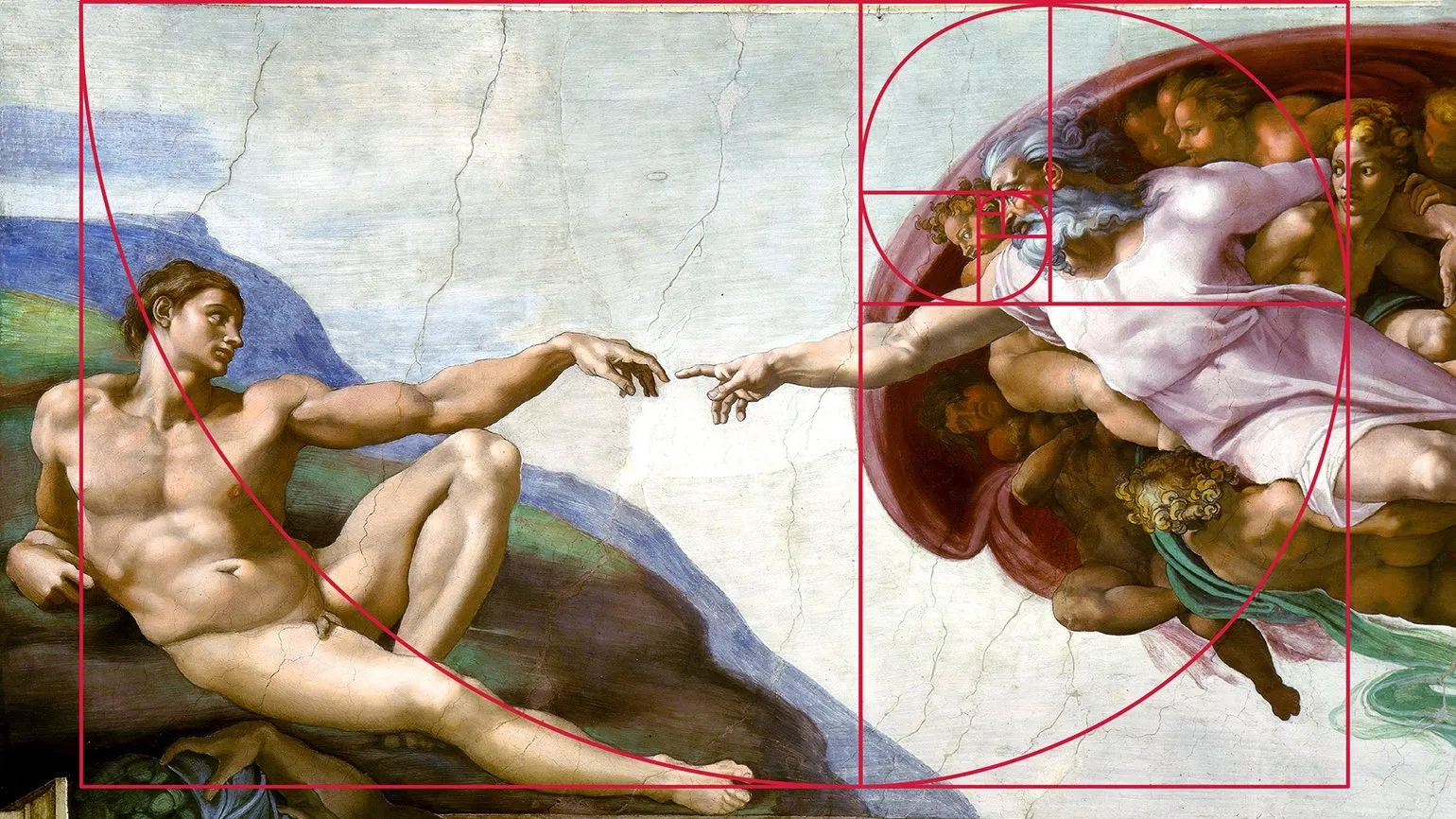
Числа Фибоначчи оказывают влияние не только на ученых, но и на художников. Принципы золотого сечения, основанные на последовательности Фибоначчи, нашли свое применение в ряде знаменитых произведений искусства. Например, фреска Микеланджело «Сотворение Адама» демонстрирует гармонию пропорций, основанную на этих математических концепциях. Использование чисел Фибоначчи в искусстве подчеркивает связь между математикой и эстетикой, что вдохновляет творческих людей на создание уникальных и гармоничных произведений.

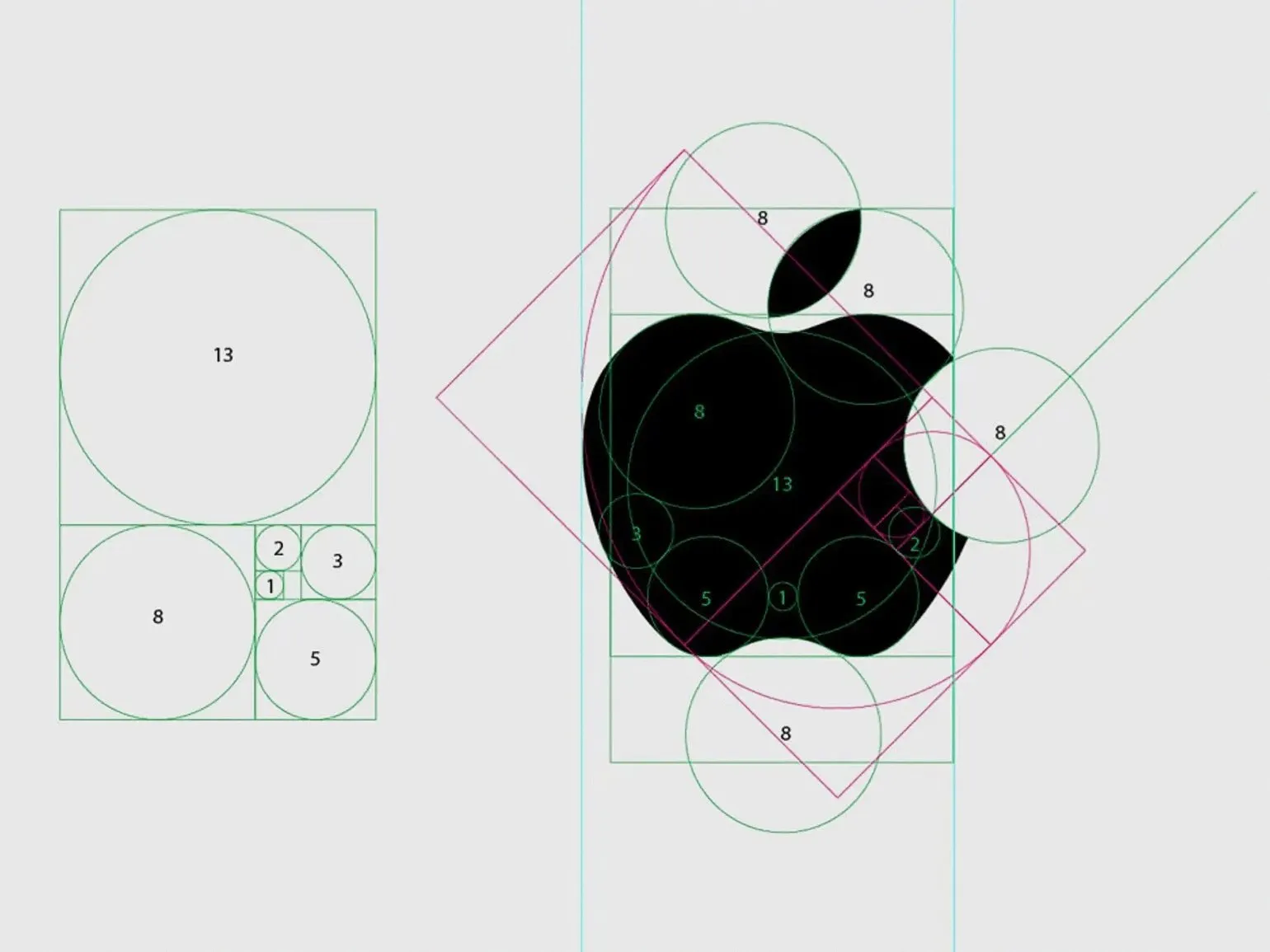
Современные дизайнеры активно применяют золотое сечение в процессе создания логотипов и графических макетов, что позволяет достичь гармонии и эстетической привлекательности. Примером может служить логотип компании Apple, в котором используются элементы, основанные на числах Фибоначчи. Золотое сечение помогает создавать сбалансированные и визуально привлекательные композиции, что делает его незаменимым инструментом в арсенале каждого дизайнера.

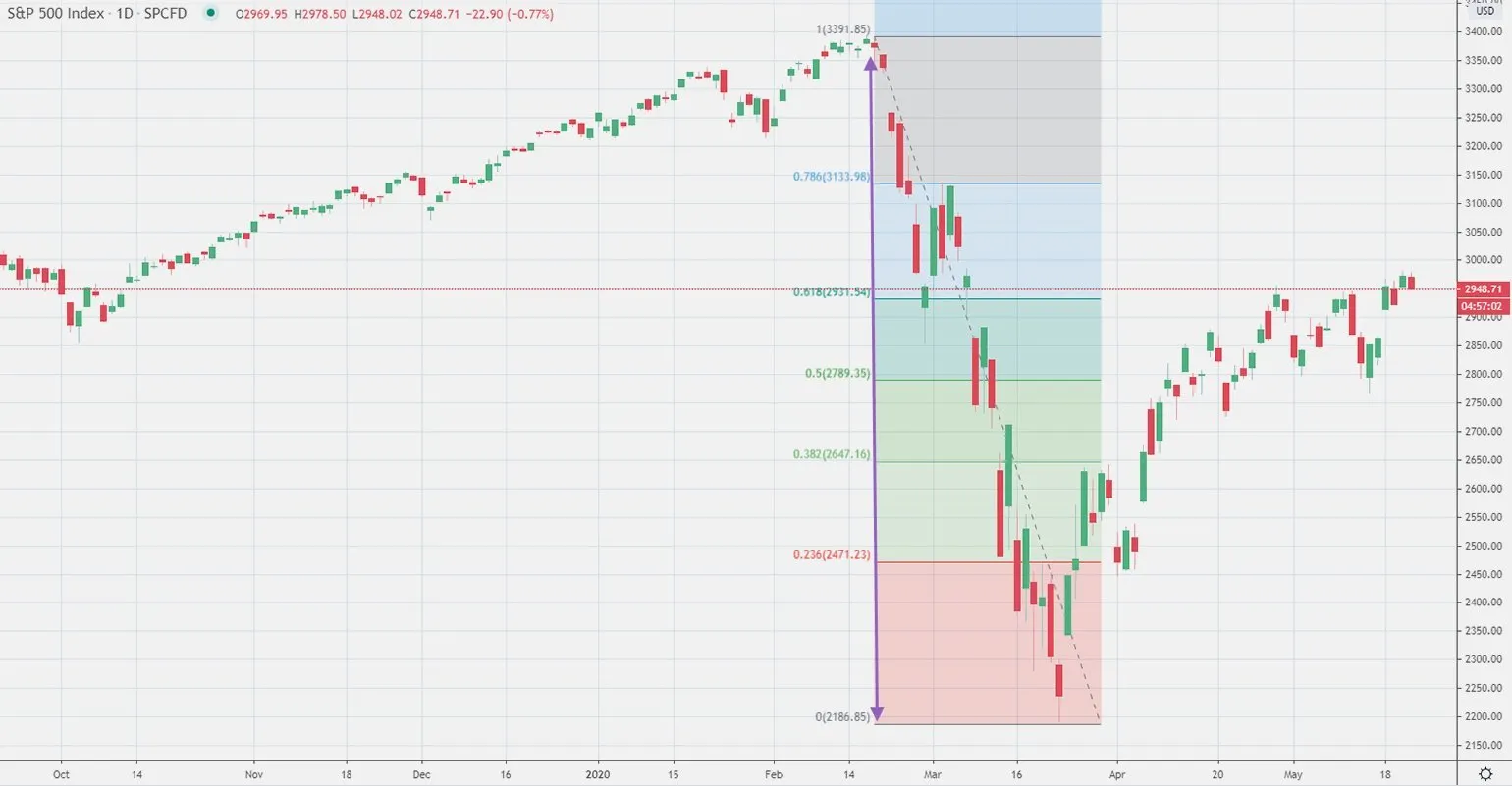
В финансовом секторе трейдеры применяют числа Фибоначчи для анализа и прогнозирования цен на акции. Уровни Фибоначчи, такие как 38,2%, 50% и 61,8%, служат инструментом для определения потенциальных точек разворота на рынке. Использование этих уровней позволяет трейдерам более точно выявлять области поддержки и сопротивления, что способствует принятию обоснованных торговых решений. Таким образом, числа Фибоначчи играют ключевую роль в техническом анализе финансовых инструментов, позволяя трейдерам оптимизировать свои стратегии и повысить вероятность успешных сделок.

В программировании последовательность Фибоначчи находит широкое применение, в том числе и в области криптографии. Одним из примеров является генерация псевдослучайных чисел, которая основана на уникальных свойствах данной последовательности. Использование последовательности Фибоначчи позволяет создавать алгоритмы, обеспечивающие безопасность и стойкость к атакам, что делает её важным инструментом в разработке современных криптографических систем.

Алгоритм на Python для вычисления чисел Фибоначчи может быть реализован с помощью рекурсивной функции. Эта функция принимает номер элемента последовательности Фибоначчи и возвращает его значение. Рекурсивный подход позволяет эффективно находить числа Фибоначчи, хотя для больших индексов может потребоваться оптимизация. Использование мемоизации или итеративного метода может значительно ускорить процесс вычисления.

• Получает на вход номер числа в последовательности Фибоначчи.
• Возвращает единицу, если номер 1 или 2.
• Если номер больше 2, рекурсивно возвращает сумму двух предыдущих чисел.

Числа Фибоначчи имеют значительное влияние на множество аспектов нашей жизни, включая природные процессы, финансовые стратегии и формы художественного самовыражения. Эти последовательности чисел проявляются в природе, например, в структуре растений и спиралях раковин, а также используются в финансовом анализе для прогнозирования рыночных движений. В искусстве и архитектуре числа Фибоначчи применяются для достижения гармонии и баланса, что подчеркивает их универсальность и важность в различных сферах.

Значение чисел Фибоначчи в природе и науке

В процессе подготовки этого материала редактор вспомнил о замечательном диалоге из популярной детской книги «В лабиринте чисел». Этот разговор наглядно демонстрирует значимость чисел Фибоначчи и их повсеместное присутствие в нашей жизни. Числа Фибоначчи не только fascinируют, но и находят применение в различных областях, от природы до искусства и науки. Их уникальные свойства позволяют лучше понять структуру и порядок в окружающем мире.

Ари объяснила, что числа Фибоначчи обладают множеством удивительных свойств. Например, в природе они влияют на рост деревьев. Если на втором году жизни дерева образуется два ответвления, то на третьем их станет три, на четвёртом — пять, затем восемь, тринадцать и так далее. Все эти числа принадлежат знаменитому ряду Фибоначчи. Этот ряд также определяет расположение листьев на ветвях, количество завитков в семенах подсолнуха и чешуйках сосновой шишки. Природа активно применяет числа Фибоначчи в своих формах и структурах, что делает их важными для понимания биологических процессов и закономерностей. Числа Фибоначчи не только интересны с точки зрения математики, но и играют ключевую роль в экологии и ботанике.

Чит неожиданно задал вопрос: «А как насчёт людей? Используют ли они это знание?»

Числа Фибоначчи долгое время оставались недооцененными, и лишь в XX веке человечество осознало их истинную мощь. Эти последовательности находят широкое применение в вычислительной технике и алгоритмах, подобно булевой алгебре. Кроме того, числа Фибоначчи играют важную роль в решении сложных математических задач. Их влияние на современные технологии и науку трудно переоценить. Важно отметить, что числовой ряд Фибоначчи продолжает открывать новые горизонты, и его потенциал в будущем остается неограниченным. Каждое открытие в этой области имеет значительное значение для дальнейшего развития науки и технологий.

Числа Фибоначчи представляют собой последовательность, которая имеет не только увлекательное математическое значение, но и практическое применение в различных сферах. Эти числа находят свое место в биологии, например, в структуре растений и численности популяций, а также в архитектуре, где отражают гармонию и пропорции. Кроме того, последовательность Фибоначчи используется в искусственном интеллекте для алгоритмических решений и оптимизации. Изучение чисел Фибоначчи открывает новые горизонты в разных науках и технологиях, подтверждая их универсальную ценность.

Обязательно ознакомьтесь с дополнительной информацией:

• Что такое факториал и как его вычислить
• Тест: рэпер, классик или нейросеть?
• Что такое нейросеть и как она работает