Что такое логарифм: основные свойства и примеры решения логарифмических задач / Skillbox Media

Содержание:

• Что такое логарифм
• Что такое натуральный логарифм
• Какие ещё есть виды логарифмов: десятичный и двоичный
• Свойства и формулы логарифмов
• Как решать логарифмы: попробуйте сами
• Как считать логарифмы в Python

Перед тем как перейти к обсуждению, давайте обновим наши знания и решим несколько типичных задач.

• Чему равен log3 81?
• А lg 2 × lb 10?
• А сумма log216 2 + log216 3?

Если вы без труда решили все три примера в уме, не прибегая к помощи калькулятора, можете смело переходить к заключительной части. А для тех, кто не совсем уверен в своих знаниях или немного подзабыл материал из школьной программы, предлагаем краткое повторение основных понятий. Это займет всего пять минут и поможет вам восстановить уверенность в своих математических навыках.

Что такое логарифм

Логарифм можно рассматривать как обратную операцию к возведению в степень. Например, в выражении 2^3 = 8, число 2 является основанием степени, 3 — показателем степени, а результатом возведения в степень является 8. Логарифм позволяет нам определить, какой показатель степени необходим, чтобы получить заданное число, в данном случае 8. Таким образом, логарифм 8 по основанию 2 равен 3. Понимание логарифмов имеет важное значение в математике и широко используется в различных областях, таких как физика, экономика и информатика.

• 2 — основание степени;
• 3 — показатель степени;
• 8 — результат возведения в степень.

Возведение в степень имеет два обратных процесса. Первое из них — извлечение корня, при котором мы находим основание. Второе — логарифмирование, в котором определяется показатель степени. Эти операции играют важную роль в математике и используются в различных областях, включая алгебру, анализ и прикладные науки. Понимание этих концепций необходимо для решения более сложных задач и работы с экспоненциальными функциями.

Выражение 23 = 8 можно преобразовать в логарифмическую форму, получая log2 8 = 3. Это указывает на то, что 2 в степени 3 равно 8. Логарифмы являются важным инструментом в математике, так как они позволяют упростить сложные вычисления и анализировать экспоненциальные функции.

Логарифм — это математическая функция, которая определяет, в какую степень необходимо возвести основание (в данном случае 2), чтобы получить заданное число (в данном случае 8). В контексте логарифмов, если мы говорим о логарифме числа 8 по основанию 2, то это означает, что мы ищем такое значение, которое, будучи возведённым в степень 2, даст результат 8. В данном примере логарифм 8 по основанию 2 равен 3, так как 2 в степени 3 равно 8. Понимание логарифмов является важным аспектом математики, используемым в различных областях, включая науку, инженерию и экономику.

Форма записи может показаться неинтуитивной, и начинающим пользователям часто сложно различить основание и степень. Для упрощения процесса запоминания рекомендуем использовать простое правило: основание всегда обозначается внизу, а степень — вверху. Это поможет избежать путаницы и упростит работу с математическими выражениями. Правильное понимание и использование данной схемы значительно облегчит изучение и применение степеней в различных задачах.

Основание логарифма, аналогично основанию степени, располагается в нижней части логарифмического выражения.

Для улучшения понимания структуры записи, ознакомьтесь с приведёнными выражениями и постарайтесь осознать их значение. Это поможет вам лучше запомнить и применять информацию в будущем. Обратите внимание на ключевые элементы и связи между ними, чтобы упростить процесс запоминания и усвоения материала.

• log3 9 = 2
• log4 64 = 3
• log5 625 = 4
• log7 343 = 3
• log10 100 = 2
• log2 128 = 7
• log2 0,25 = −2
• log625 125 = 0,75

Запись logAB интерпретируется как логарифм числа B по основанию A. Логарифмы являются важным инструментом в математике и используются для решения различных уравнений и анализа данных. Понимание логарифмов и их свойств позволяет эффективно работать с экспоненциальными функциями и упрощать сложные вычисления.

Что такое натуральный логарифм

Основание логарифма является ключевым элементом в логарифмических функциях. Наличие общего основания у различных логарифмов позволяет выполнять операции между ними, что значительно упрощает решение математических задач. Понимание этого аспекта логарифмов играет важную роль в их применении в algebra, анализе данных и других областях науки.

Число Эйлера (e) является основанием натурального логарифма. Это иррациональное число, которое примерно равно 2,71828. В математике и различных прикладных науках число e играет ключевую роль, особенно в теории пределов, дифференциальных уравнениях и финансовых расчетах. Понимание числа Эйлера и его свойств необходимо для глубокого изучения логарифмических и экспоненциальных функций, что делает его важным элементом в математическом анализе.

Иррациональные числа — это числовые значения, которые невозможно выразить в виде простых дробей, где числитель и знаменатель являются целыми числами. Важно отметить, что знаменатель в этой дроби не может равняться нулю. Иррациональные числа включают в себя такие известные значения, как √2, π и e, и играют ключевую роль в различных областях математики, включая геометрию и анализ. Эти числа являются противоположностью рациональных, которые могут быть представлены в виде дробей. Понимание иррациональных чисел важно для глубокого изучения числовых систем и их свойств.

Число 0,333… является рациональным, так как его можно выразить в виде дроби 1/3. В отличие от него, числа такие как Пи и квадратный корень из 2 относятся к иррациональным, так как их нельзя представить в виде простых дробей. Рациональные числа могут быть представлены как конечные или бесконечные периодические десятичные дроби, тогда как иррациональные числа имеют бесконечные непериодические десятичные представления. Это различие имеет важное значение в математике и помогает лучше понять свойства чисел.

Натуральные логарифмы играют важную роль в математике и многих других науках. Для их обозначения существует специальный способ записи: ln x. Это обозначение эквивалентно loge x, где e представляет собой основание натурального логарифма, приблизительно равное 2.71828. Использование ln x упрощает математические выражения и делает их более удобными для анализа. Понимание этого обозначения является ключевым для решения задач, связанных с экспоненциальным ростом и другими математическими концепциями.

Представим себе кристалл с начальным весом 1 кг, который увеличивает свою массу на 100% в год. На первый взгляд, можно предположить, что через год его вес составит 2 кг. Однако это утверждение требует уточнения, поскольку рост кристалла не всегда происходит линейно. Фактически, если кристалл продолжает расти с той же скоростью, его вес через год составит 2 кг, но дальнейший рост будет иметь свои особенности. Это связано с тем, что при постоянном процентном увеличении массы, вес кристалла будет удваиваться каждый год. Таким образом, через два года его вес достигнет 4 кг, а через три года — 8 кг. Это пример экспоненциального роста, который иллюстрирует, как быстро могут увеличиваться размеры объектов при постоянном процентном увеличении.

Каждая новая часть кристалла начинает развивать свою собственную массу. Когда масса кристалла достигает 1,1 кг, его прирост составляет 1,1 кг в год, а при массе 1,5 кг — прирост увеличивается до 1,5 кг в год. Исследования математиков показывают, что через год масса кристалла может составить e, что приблизительно равно 2,71828 кг. Это демонстрирует экспоненциальный рост кристаллов, который представляет интерес для изучения в различных областях науки.

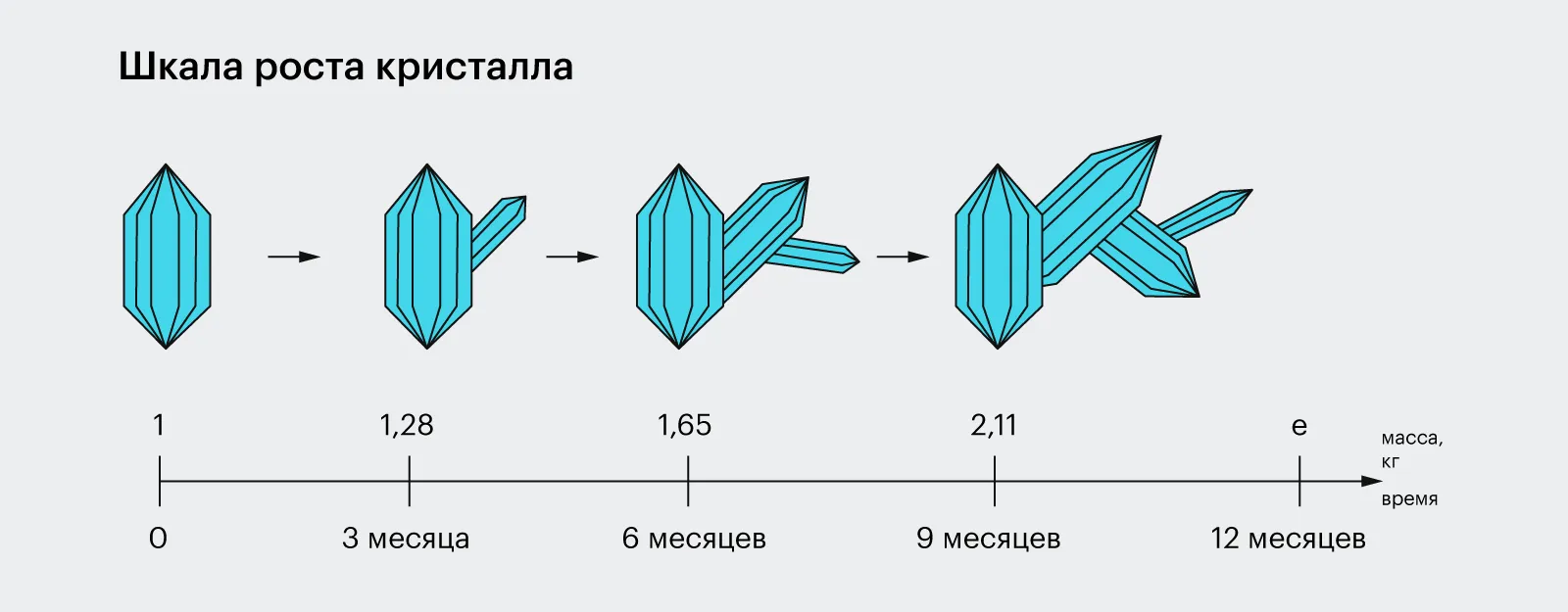
Экспоненциальный рост наблюдается в различных процессах, таких как размножение бактерий, увеличение популяций, рост доходов, накопление снежных комьев, распад радиоактивных веществ и охлаждение напитков. Этот тип роста характеризуется быстрым увеличением, когда каждое новое значение становится значительно больше предыдущего. Экспоненциальные процессы имеют важное значение в биологии, экономике и физике, так как они позволяют предсказать поведение систем в условиях, когда ресурсы или время ограничены. Понимание экспоненциального роста помогает в анализе и прогнозировании различных явлений в природе и обществе.

Для определения массы кристалла через три, пять или десять лет необходимо возвести число e в соответствующую степень. Этот математический подход позволяет точно оценить изменения в массе кристалла с течением времени.

e3 составляет примерно 20,0855 килограмма. Это значение важно для расчетов в различных областях, включая физику и инженерные науки. Понимание и правильное использование единиц измерения, таких как килограммы, необходимо для точности в научных исследованиях и практических приложениях.

e5 составляет примерно 148,4132 килограмма. Этот показатель может быть важен в различных контекстах, таких как физические расчеты, спортивные достижения или при измерении веса для научных исследований. Правильное понимание и использование единиц измерения, таких как килограммы, играет ключевую роль в точности результатов и интерпретации данных.

e10 составляет примерно 22 026,47 кг.

Чтобы определить, когда кристалл достигнет веса в одну тонну, необходимо составить уравнение. Для этого следует учесть исходные параметры, такие как начальная масса кристалла, скорость его роста и факторы, влияющие на увеличение массы. Рассмотрим все необходимые переменные и их взаимосвязь, чтобы получить точное уравнение. Это позволит точно предсказать момент, когда масса кристалла станет равной одной тонне.

Экспоненциальный рост — это процесс, при котором величина увеличивается с течением времени, пропорционально её текущему значению. Этот принцип часто наблюдается в финансах, биологии и технологиях. В экономике экспоненциальный рост может быть иллюстрирован увеличением инвестиций, где доходы растут на постоянный процент. В биологии экспоненциальный рост проявляется в размножении популяций, когда количество особей возрастает с каждым поколением. В технологической сфере экспоненциальный рост наблюдается в увеличении вычислительных мощностей, например, по закону Мура. Понимание экспоненциального роста критически важно для прогнозирования будущих тенденций, управления ресурсами и разработки стратегий развития. Этот концепт также подчеркивает важность устойчивого подхода, чтобы предотвратить негативные последствия резкого увеличения численности или потребления ресурсов.

Для нахождения показателя степени, зная основание и результат возведения в степень, мы можем воспользоваться понятием логарифма. Это значит, что если основание равно e, а результат составляет 1000, тогда мы можем записать уравнение x = loge 1000. В более привычной форме это будет выглядеть как x = ln 1000. Логарифмы играют ключевую роль в математике и используются в различных областях, включая науку и финансы, для упрощения вычислений и решения уравнений.

Подставив данные в калькулятор, мы получаем, что x ≈ 6,9. Это означает, что кристаллу потребуется примерно 6,9 лет для достижения массы в одну тонну.

Какие ещё есть виды логарифмов: десятичный и двоичный

Десятичный логарифм, основание которого равно 10, обозначается как lg x. Этот тип логарифма широко используется благодаря своей простоте в расчетах, особенно при работе с круглыми числами. Десятичный логарифм находит применение в различных областях, таких как математика, физика и экономика, благодаря своей способности упрощать сложные вычисления.

Двоичный логарифм — это логарифм с основанием 2, который обозначается как lb x. Он широко используется в программировании и компьютерных науках, поскольку компьютеры функционируют на основе двоичной системы счисления. Понимание двоичного логарифма имеет важное значение для оптимизации алгоритмов и анализа их сложности. Например, в таких областях, как обработка данных и системное программирование, знание свойств двоичного логарифма позволяет разработчикам более эффективно управлять ресурсами и улучшать производительность приложений.

Свойства и формулы логарифмов

Логарифмические операции имеют свои ограничения, но если вы освоите их и запомните основные правила, выполнение логарифмических задач станет для вас простым и быстрым процессом. Умение работать с логарифмами значительно упростит решение математических задач и повысит вашу уверенность в этом разделе математики.

Логарифмы имеют определенные ограничения. Основание и аргумент логарифма должны быть положительными числами. Кроме того, основание не должно равняться единице. В математической записи это выражается следующим образом:

Рассмотрим свойства логарифмов. Эти свойства действуют в обоих направлениях, что позволяет использовать их как слева направо, так и справа налево. Логарифмические операции являются важными инструментами в математике, позволяя упрощать сложные выражения и решать уравнения. Понимание этих свойств поможет лучше ориентироваться в математических задачах и эффективно использовать логарифмы в различных контекстах.

Логарифм единицы по любому основанию всегда равен нулю. Это важное свойство логарифмов, которое позволяет упростить множество математических задач. Для любого положительного числа a, где a не равно 1, логарифм единицы по основанию a формально записывается как log_a(1) = 0. Это следует из определения логарифма, так как a в степени 0 всегда равно 1. Понимание этого свойства является основой для решения более сложных логарифмических уравнений и неравенств.

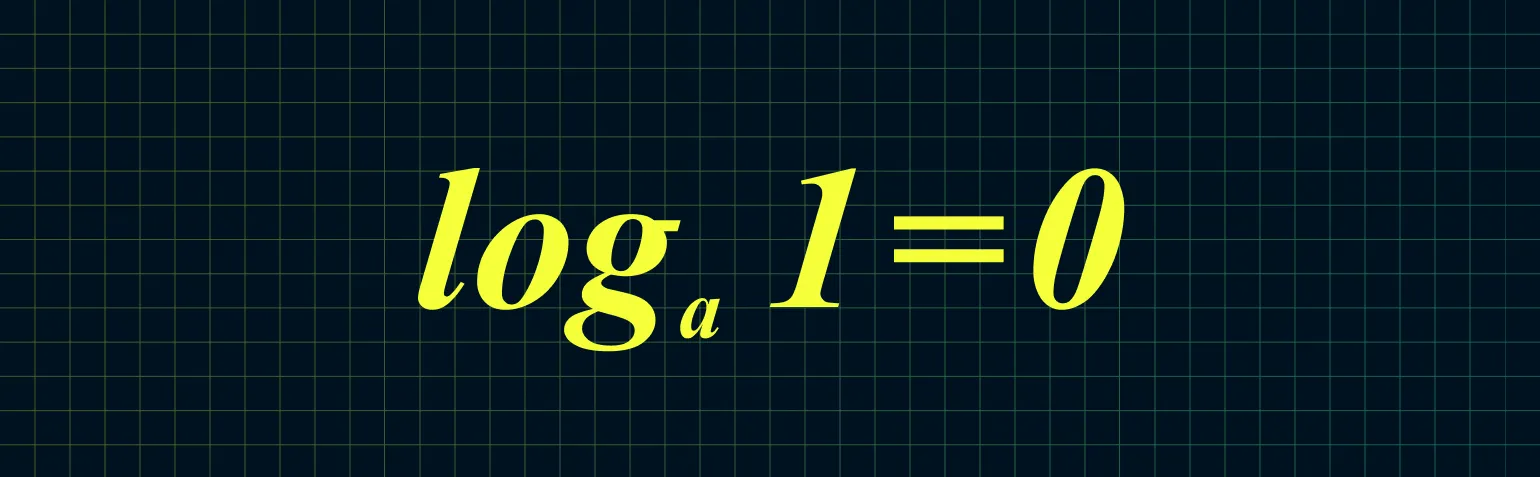
Конечно, я готов помочь вам с переработкой текста. Пожалуйста, предоставьте исходный текст, который нужно отредактировать.

Логарифм с основанием 17 от 1 равен 0. Это утверждение основано на свойствах логарифмов. Логарифм числа обозначает степень, в которую основание должно быть возведено, чтобы получить это число. Поскольку любое число, возведенное в нулевую степень, равно 1, логарифм 1 с любым положительным основанием всегда равен 0. Таким образом, log17 1 = 0 является верным математическим утверждением.

Логарифм, в котором число и основание совпадают, всегда равен единице. Это важное свойство логарифмической функции, которое используется в различных математических задачах и приложениях. Понимание этого правила позволяет упростить решение уравнений и анализ функций. Например, если у вас есть логарифм с основанием 5 и числом 5, то результат будет равен 1. Это свойство можно применять в различных областях, включая алгебру и анализ данных.

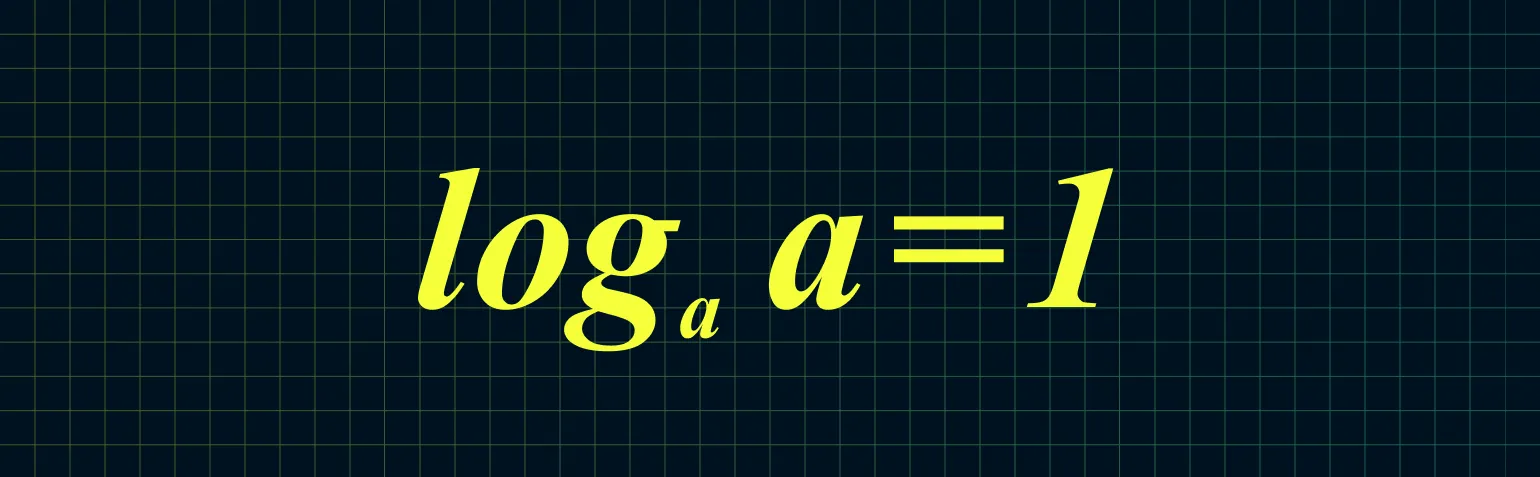
log17 17 = 1 является примером логарифмического уравнения, где логарифм числа 17 по основанию 17 равен 1. Это свойство логарифмов объясняется тем, что любое число, возведенное в степень 1, дает само себя. Логарифмическая функция широко используется в математике, физике и инженерии для решения различных задач. Понимание основ логарифмов, таких как это уравнение, помогает лучше осваивать более сложные темы, включая экспоненциальные функции и их приложения. Логарифмы также играют важную роль в анализе данных и статистике, где они помогают в преобразовании и интерпретации больших чисел.

Основное логарифмическое тождество является важным принципом в математике, который описывает свойства логарифмов. Это тождество утверждает, что логарифм произведения двух чисел равен сумме логарифмов этих чисел. Формально это можно записать как log_a(b * c) = log_a(b) + log_a(c), где a — основание логарифма, b и c — положительные числа. Данное тождество часто используется для упрощения вычислений и преобразования выражений в алгебре. Понимание основного логарифмического тождества важно для решения сложных математических задач и анализа экспоненциальных процессов. Применение этого тождества на практике помогает в различных областях, таких как экономика, физика и информатика, где логарифмы играют ключевую роль в моделировании и анализе данных.

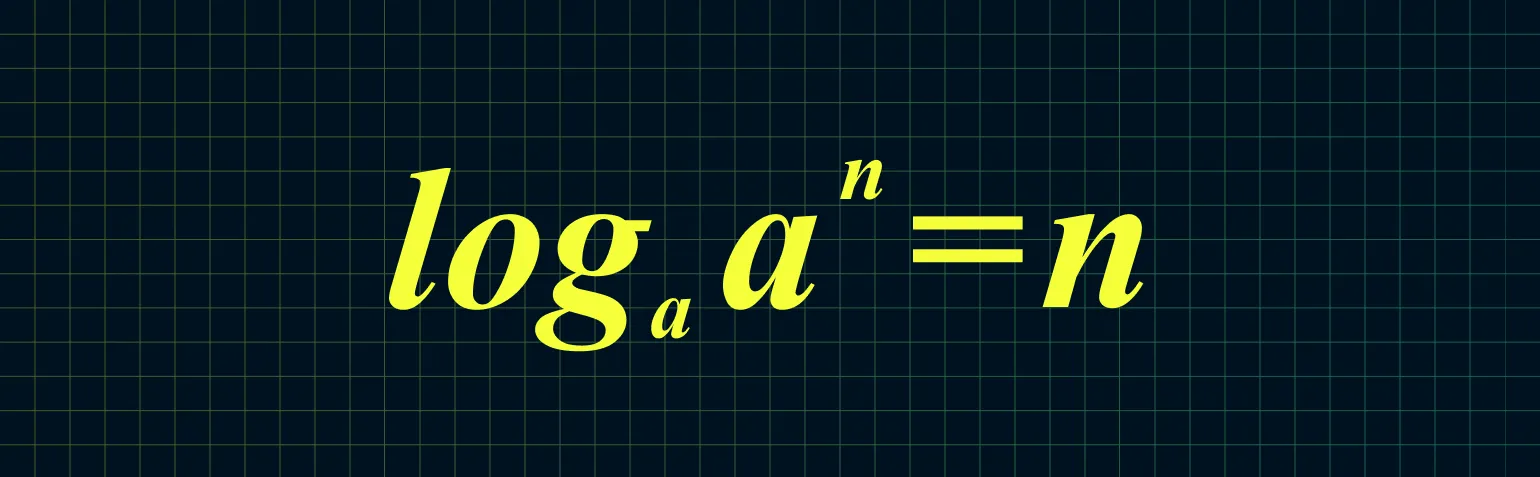
Логарифм числа 17 по основанию 5 равен 175.

Логарифм произведения чисел равен сумме их логарифмов. Это важное свойство логарифмов, которое позволяет упростить вычисления и анализ данных. Если a и b — положительные числа, то логарифм их произведения можно выразить следующим образом: log(ab) = log(a) + log(b). Это правило помогает в различных областях, таких как математика, физика и экономика, где необходимо работать с большими числами или сложными вычислениями. Использование данного свойства логарифмов значительно упрощает процесс решения уравнений и выполнения математических операций.

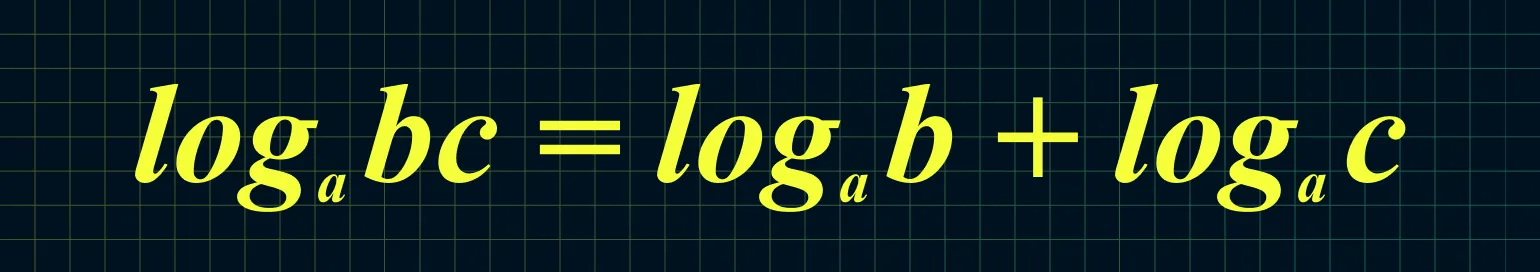
Пример: log5 12,5 + log5 10 = log5 (12,5 × 10) = log5 125 = 3. В данном выражении мы видим, как применяются свойства логарифмов. Сумма логарифмов с одинаковым основанием равна логарифму произведения аргументов. Это важное свойство позволяет упрощать вычисления и решать сложные уравнения с логарифмами. При использовании данного правила следует помнить, что основание логарифма должно быть одинаковым для всех логарифмов в выражении. В этом случае мы имеем дело с логарифмом по основанию 5. Применение таких свойств логарифмов значительно упрощает процесс работы с математическими задачами и делает их более понятными.

Логарифм дроби определяется как разность логарифмов числителя и знаменателя. Это свойство логарифмов позволяет упростить вычисления и преобразования в математике. Если у вас есть дробь, состоящая из числителя и знаменателя, то логарифм этой дроби можно выразить следующим образом: логарифм от A/B равен логарифму A минус логарифм B. Это правило является основополагающим в алгебре и часто используется в различных областях науки и техники для анализа данных и решения уравнений. Понимание этого свойства помогает лучше ориентироваться в логарифмических функциях и упрощает процесс работы с ними.

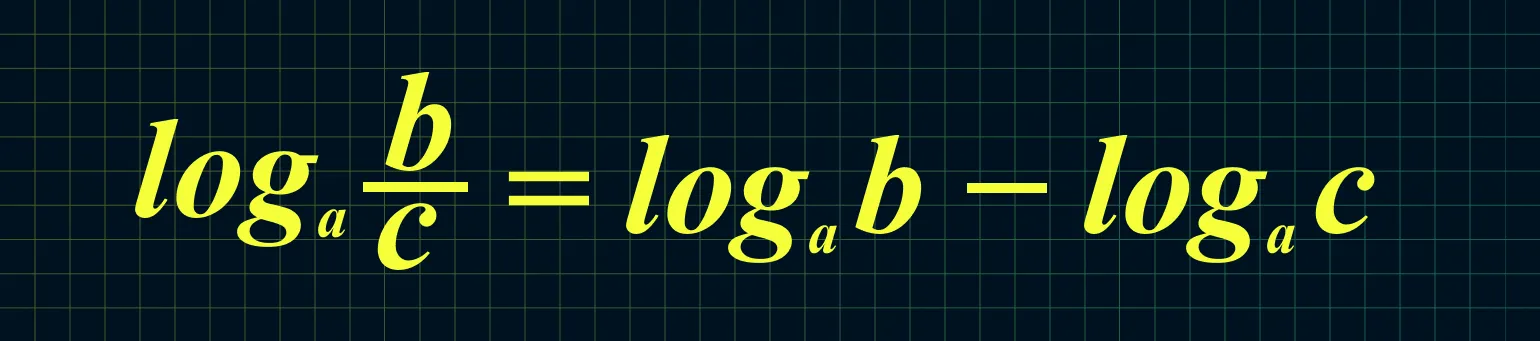
Рассмотрим пример преобразования логарифмического выражения: log3 63 − log3 7. Сначала используем свойство логарифмов, которое позволяет вычитать логарифмы с одинаковым основанием. Это дает нам: log3 (63/7). Далее упрощаем дробь: 63/7 равно 9. Таким образом, мы можем выразить это как log3 9. Поскольку 9 является 3 в квадрате, мы можем записать результат как log3 (3^2). В соответствии с основным свойством логарифмов, это упрощается до 2. Таким образом, окончательный ответ равен 2.

При возведении основания или аргумента в степень их можно удобно вынести перед логарифмом. Это свойство логарифмов позволяет упростить вычисления и сделать выражения более удобными для анализа. Например, если у вас есть логарифм с основанием a и аргументом b, возведённым в степень n, то это можно записать как n умножить на логарифм a от b. Использование этого свойства значительно упрощает работу с логарифмическими уравнениями и неравенствами. Правильное применение данных свойств помогает в решении сложных математических задач и улучшает понимание логарифмических функций.

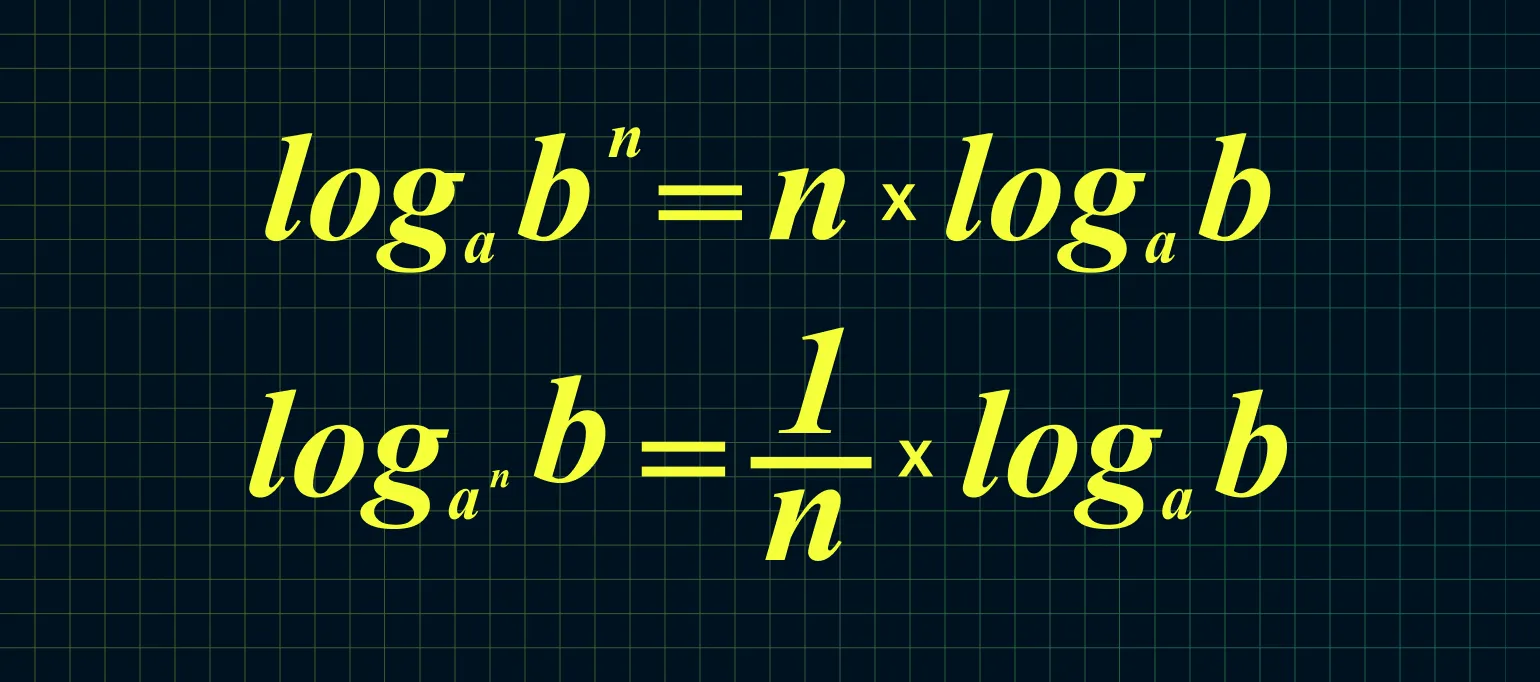
Из приведенных двух формул можно сделать следующие выводы.

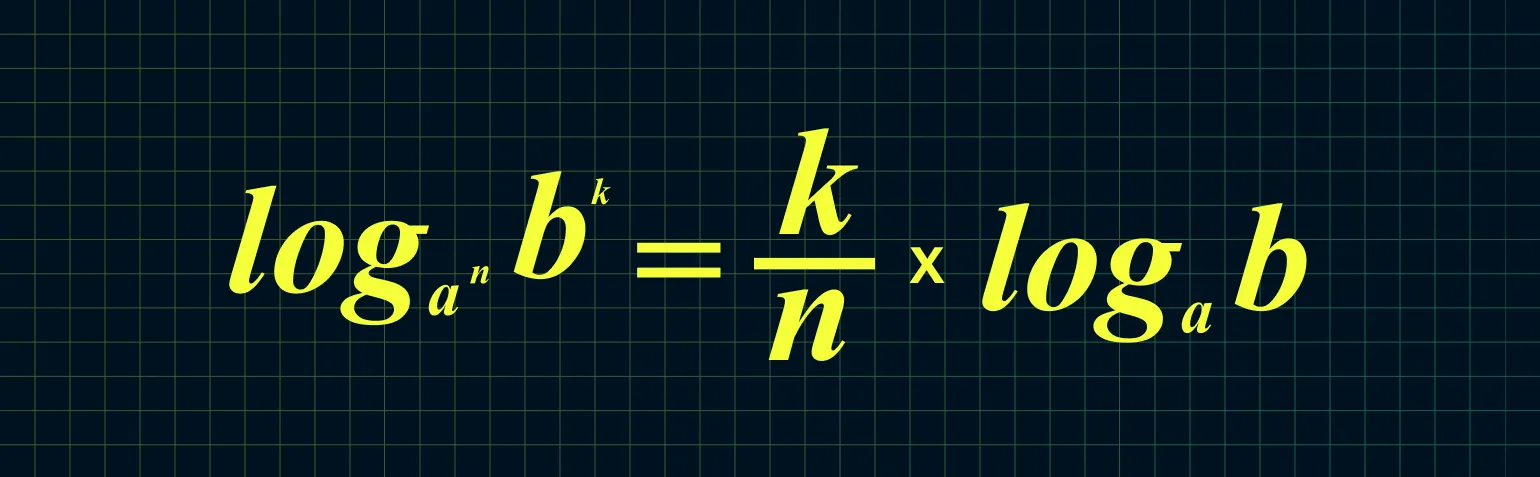
Пример: log23 49 = (9/3) × log2 4 = 3 × 2 = 6. Это демонстрирует использование свойств логарифмов для упрощения выражений. Логарифмы позволяют преобразовывать сложные вычисления в более простые, что делает их незаменимым инструментом в математике и смежных областях. Понимание этих свойств важно для решения уравнений и анализа функций.

Если выбранное основание логарифма оказывается неудобным, его можно легко изменить. Изменение основания логарифма позволяет адаптировать расчет к конкретным условиям задачи. Например, для упрощения вычислений можно использовать формулу изменения основания логарифма, которая позволяет преобразовать логарифм с одного основания на другое. Это особенно полезно в математике и смежных областях, где требуется работать с различными системами счисления или единицами измерения.

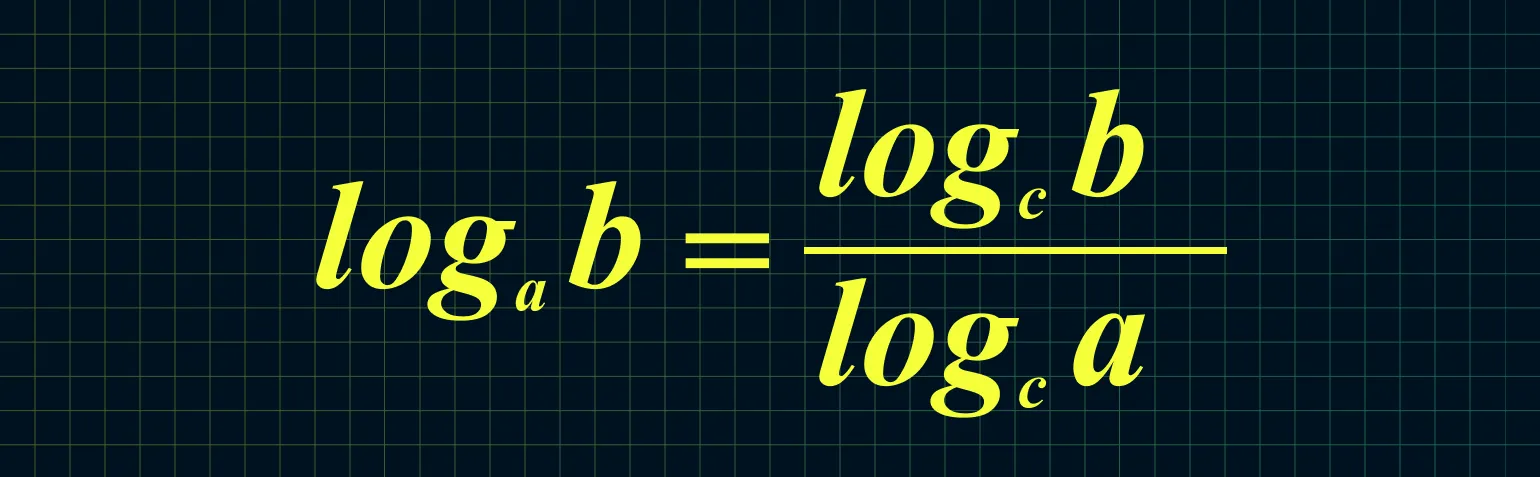
Для вычисления логарифма по основанию 25 от числа 125 можно воспользоваться свойством логарифмов. Применим следующее соотношение: log25 125 = log5 125 / log5 25. Выполнив расчет, получаем log5 125 = 3, так как 5 в степени 3 дает 125, и log5 25 = 2, так как 5 в степени 2 равно 25. Делая деление, получаем 3 / 2, что равно 1,5. Таким образом, log25 125 равно 1,5.

Согласно данной формуле, мы можем изменить местами основание и аргумент, что позволяет нам записать это в следующем виде:

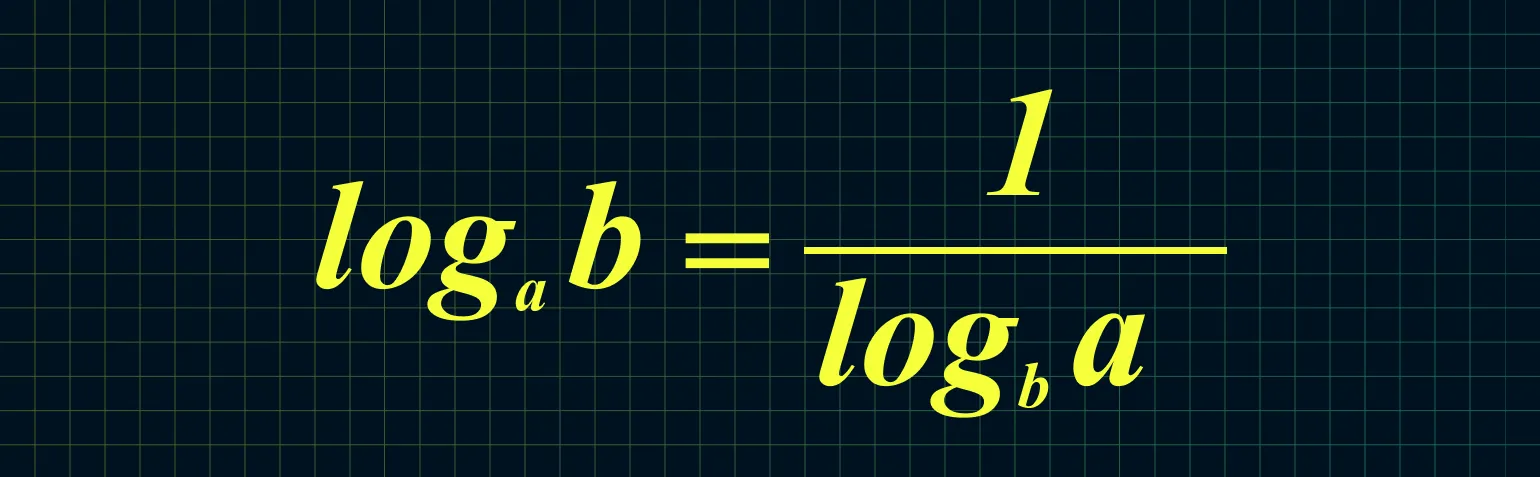
Пример вычисления логарифма: log16 4 равен 1/log4 16, что в свою очередь упрощается до 1/2, равного 0,5. Логарифмы являются важным инструментом в математике, позволяющим решать уравнения, связанные с экспонентами. Понимание свойств логарифмов, таких как изменение основания и взаимосвязь между логарифмами, способствует более глубокому пониманию алгебры и анализа. Использование логарифмических функций в научных и инженерных расчетах позволяет упростить сложные вычисления и анализ данных.

Как решать логарифмы: попробуйте сами

Теперь вернемся к задачам, которые были поставлены в начале статьи. Обсудим их более подробно и проанализируем, как их можно эффективно решить. Каждая задача требует особого внимания и подхода, что позволит достичь наилучших результатов. Разберем ключевые аспекты и возможные стратегии для выполнения этих задач, чтобы обеспечить максимальную эффективность и результативность.

Пример 1:

В современном мире, где технологии стремительно развиваются, создание качественного контента становится одной из важнейших задач для бизнеса. Качественный контент не только привлекает внимание потенциальных клиентов, но и способствует повышению позиций сайта в поисковых системах. Важно, чтобы текст был не только информативным, но и оптимизированным под SEO. Это значит, что необходимо использовать ключевые слова, соответствующие тематике, а также следить за структурой и читаемостью текста.

Оптимизированный контент помогает улучшить видимость сайта, что, в свою очередь, приводит к увеличению трафика и росту конверсий. Эффективные стратегии SEO включают в себя правильный выбор ключевых фраз, создание уникального и интересного контента, а также регулярное обновление информации на сайте. В результате, качественный контент становится мощным инструментом для достижения бизнес-целей и повышения конкурентоспособности на рынке.

Вспомните, что 81 соответствует 92, а 9 — это 32. Исходя из этого, можно сделать выводы о взаимосвязях между этими числами. Понимание таких соотношений может быть полезным в различных математических задачах и исследованиях. Используйте эти связи для более глубокого анализа числовых значений и их применения в практических ситуациях.

log3 81 равняется log3 92, что также можно выразить как log3 (32 + 2) и упрощается до log3 34. Это равенство демонстрирует свойства логарифмов, позволяя работать с ними более эффективно. Логарифмы являются важным инструментом в математике, особенно в алгебре и аналитической геометрии. Упрощая выражения с логарифмами, можно легче решать уравнения и анализировать функции.

Логарифм больше не вызывает у нас затруднений. Применяя свойства степеней, мы можем вынести четвёрку за скобки.

Логарифм по основанию 3 от числа 34 можно выразить через логарифм по тому же основанию от числа 3. Это выглядит следующим образом: log3 34 равно 4, умноженному на log3 3. Поскольку log3 3 равно 1, мы получаем: 4 умноженное на 1, что в итоге равно 4. Таким образом, log3 34 = 4.

Пример 2 является важным элементом для понимания конкретной темы. Он иллюстрирует ключевые аспекты и служит наглядным примером, который помогает лучше усвоить материал. Применение примера 2 позволяет углубить знания и улучшить восприятие информации. Важно учитывать, что примеры являются эффективным инструментом для объяснения сложных концепций. Они делают материал более доступным и понятным для аудитории. Использование примера 2 в учебном процессе способствует активному обучению и развитию критического мышления. Такой подход помогает закрепить изучаемый материал и повысить его усваиваемость.

Переведем аббревиатуры и сокращенные записи в их полное написание, чтобы обеспечить ясность и понимание текста. Это поможет читателю лучше воспринимать информацию и избежать недоразумений. Полное раскрытие сокращений также способствует улучшению SEO-оптимизации, так как поисковые системы лучше индексируют текст, содержащий полные формулировки. Правильно оформленный и структурированный контент повышает его доступность и удобство для пользователей.

Формула lg 2 × lb 10 = log10 2 × log2 10 показывает связь между различными логарифмическими функциями. Здесь lg обозначает десятичный логарифм, а lb — двоичный логарифм. Важно понимать, что логарифмы позволяют преобразовывать множества чисел в более управляемый формат, что особенно полезно в математических расчетах и информатике. Изучение логарифмов помогает лучше осознать отношения между величинами и их масштабами. Эта формула иллюстрирует, как различные основания логарифмов могут быть связаны друг с другом. Понимание этих взаимосвязей критически важно для решения сложных задач в математике и других науках.

Чтобы выполнить преобразование обоих логарифмов к одному основанию, необходимо использовать свойства логарифмов. Логарифмы можно привести к единому основанию, применяя формулу изменения основания. Это позволит упростить выражение и сделать дальнейшие вычисления более удобными. При этом важно выбрать подходящее основание, которое обеспечит наилучшее решение задачи.

Уравнение log10 2 × log2 10 равно 1. Это можно объяснить следующим образом: log10 2 умножается на log2 10, что эквивалентно 1, поскольку log10 2 можно представить как 1/log2 10. Умножая log2 10 на 1/log2 10, мы получаем log2 10/log2 10, что равно 1. Таким образом, данное уравнение демонстрирует взаимосвязь между логарифмами в разных основаниях и их свойства. Понимание этих свойств логарифмов важно для решения задач в математике и смежных областях.

Пример 3 представляет собой важный аспект, который стоит рассмотреть более подробно. Этот пример иллюстрирует ключевые моменты и предоставляет полезные сведения, которые могут быть применены в различных ситуациях. Он демонстрирует, как правильно подходить к решению задач, а также подчеркивает важность внимания к деталям. Каждый элемент в этом примере играет свою роль и вносит вклад в общее понимание темы. Важно учитывать эти аспекты при анализе и применении информации на практике.

Используем свойство суммы для решения задач. Это свойство позволяет объединять элементы в одно целое, упрощая анализ и обработку данных. Применение свойства суммы помогает в различных областях, таких как математика, статистика и экономика, позволяя более эффективно управлять информацией и делать выводы на основе собранных данных. Рассмотрим примеры его применения для достижения наилучших результатов в решении конкретных задач.

Уравнение log216 2 + log216 3 равно log216 (2 × 3), что можно упростить до log216 6. Это демонстрирует одно из свойств логарифмов: сумма логарифмов с одинаковым основанием равна логарифму произведения аргументов. Данное свойство является полезным инструментом в математике, особенно при решении уравнений и упрощении выражений.

Рассмотрим число 216 и представим его в виде степени числа 6, используя свойства степеней. Это позволит нам упростить выражение и лучше понять, как числа взаимодействуют друг с другом в контексте математических операций. Степенное представление числа 216 будет полезно для дальнейших вычислений и анализа.

log216 6 равно log63 6 и равно 1/3 умноженное на log6 6, что в свою очередь равно 1/3 умноженное на 1, что дает 1/3. Таким образом, мы можем утверждать, что логарифм 6 по основанию 216 равен 1/3. Это свойство логарифмов демонстрирует, как можно преобразовывать выражения, используя правила логарифмической арифметики.

Ответ: 0.33.

Как считать логарифмы в Python

Для работы с логарифмическими выражениями в Python нужно сначала импортировать модуль math. Этот модуль предоставляет функции для выполнения математических операций, включая вычисление логарифмов. Чтобы использовать логарифмы, достаточно вызвать функцию `math.log()`, которая позволяет вычислить логарифм числа по основанию e, а также можно указать любое другое основание. Использование модуля math значительно упрощает работу с математическими выражениями и обеспечивает точность расчетов.

Чтобы вычислить log2 8 с использованием метода math.log, необходимо применить следующий подход. Функция math.log позволяет вычислять логарифмы с различными основаниями, включая основание 2. В данном случае, для нахождения log2 8, мы можем использовать формулу log2 8 = math.log(8, 2). Результат этого вычисления равен 3, поскольку 2 в степени 3 дает 8. Таким образом, использование метода math.log для вычисления логарифмов является простым и эффективным способом анализа экспоненциальных зависимостей.

Обратите внимание на два ключевых момента. Во-первых, в нашей функции сначала передается аргумент, а затем основание. Во-вторых, функция всегда возвращает значение в формате float, даже если итоговый результат является целым числом. Это важно учитывать при работе с функцией, чтобы избежать неожиданных ошибок в дальнейшем.

Если функция не получает основание, логарифм автоматически принимается как натуральный.

Для вычисления десятичного и двоичного логарифма используются специфические методы. Десятичный логарифм, который обозначается как log₁₀, основан на числе 10 и широко применяется в науке и инженерии. Для его вычисления можно использовать калькуляторы или логарифмические таблицы.

Двоичный логарифм, обозначаемый как log₂, основан на числе 2 и находит применение в информатике, особенно в алгоритмах и теории информации. Для его вычисления также существуют специализированные калькуляторы и программное обеспечение.

Понимание методов подсчета логарифмов важно для решения различных математических задач и анализа данных, так как логарифмы помогают упростить сложные вычисления и представляют значения в более удобной форме.

В Python существует уникальный метод, который увеличивает переданный аргумент на единицу и вычисляет натуральный логарифм полученного значения. Этот метод особенно полезен при работе с математическими и статистическими расчетами, где требуется применение логарифмических функций. Использование данного метода позволяет легко и быстро проводить необходимые вычисления, что делает его ценным инструментом для разработчиков и аналитиков данных.

Когда значение х приближается к нулю, данный метод обеспечивает более точные результаты по сравнению с использованием функции math.log(1+x). Это позволяет избежать проблем с точностью, которые могут возникать при вычислении логарифмов для малых значений. Сравните результаты, чтобы убедиться в преимуществах этого подхода.

Основные инструменты для работы с логарифмами в Python. Python предоставляет мощные библиотеки и функции для выполнения операций с логарифмами, что делает его идеальным языком программирования для математических вычислений. Используя встроенный модуль math, вы можете легко рассчитывать логарифмы различных оснований. Также доступны дополнительные библиотеки, такие как NumPy, которые расширяют возможности работы с массивами данных и позволяют производить более сложные математические операции. Знание этих инструментов позволит вам эффективно решать задачи, связанные с логарифмами, в ваших проектах на Python.

Переделанный текст:

Изучайте также:

• Математика для джунов: что нужно повторить перед собеседованием по Data Science
• Тест: как хорошо ты знаешь устройство интернета?
• ML-разработчик: кто такой, чем занимается и сколько получает