Фракталы: что это такое, какими они бывают и где они применяются / Skillbox Media

Содержание:

• Что такое фрактал
• Виды фракталов
• Геометрические фракталы
• Алгебраические фракталы
• Стохастические фракталы
• Фрактальная графика
• Фракталы в физике
• Фракталы в природе
• Вместо вывода: применение фракталов в жизни

В математике существуют явления, которые поражают своей красотой и гармонией, вызывая желание изучать их бесконечно. Одним из таких явлений являются фракталы. Эти уникальные фигуры обладают свойством самоподобия, что позволяет им рекурсивно воспроизводить себя и формировать удивительные узоры в двух- и трехмерных пространствах. Однако фракталы представляют собой не только визуальное искусство; они также открывают доступ к глубоким математическим концепциям и служат инструментом для описания естественных процессов в окружающем мире. Исследование фракталов помогает лучше понять сложные структуры, встречающиеся в природе, от форм облаков до распределения растений и даже в биологических системах.

Содержание является важным элементом любого текста, поскольку оно позволяет читателям быстро ориентироваться в его структуре и находить нужную информацию. Для оптимизации под SEO содержание должно быть четким, лаконичным и включать ключевые слова, соответствующие теме. Правильное использование заголовков и подзаголовков помогает улучшить читаемость и повысить шансы на высокие позиции в поисковых системах.

Содержание не только упрощает навигацию, но и способствует лучшему восприятию информации. При составлении содержания стоит уделить внимание последовательности и логике представления тем, чтобы читатель мог легко следовать за ходом мысли. Используйте понятные формулировки и избегайте избыточных терминов, чтобы сделать текст доступным для широкой аудитории.

Помните, что содержание должно отражать ключевые моменты вашего текста, поэтому важно обновлять его в соответствии с изменениями в основном контенте. В результате правильно оформленное содержание не только улучшит пользовательский опыт, но и повысит эффективность вашего контента в поисковых системах.

• Что такое фрактал
• Виды фракталов
• Геометрические фракталы
• Алгебраические фракталы
• Стохастические фракталы
• Фрактальные изображения
• Фракталы в физике
• Фракталы в природе

Что такое фрактал

Фрактал представляет собой фигуру, обладающую уникальным свойством самоподобия. Объект считается самоподобным, если одна или несколько его частей напоминают его целое. Интересная особенность фракталов заключается в том, что количество повторяющихся частей стремится к бесконечности, что отличает их от самоподобных геометрических фигур, имеющих конечное число звеньев, известных как предфракталы. Это свойство делает фракталы важными в различных областях, включая математику, искусство и природу, где они встречаются в виде сложных узоров и структур.

Термин «фрактал» был введён в 1975 году американским математиком Бенуа Мандельбротом, который основал его на латинском слове fractus, что переводится как «разделённый на части». В своей книге «Фрактальная геометрия природы» (The Fractal Geometry of Nature) Мандельброт представил инновационный подход к описанию сложных природных объектов, основанный на фракталах. Обычные евклидовы фигуры, такие как прямые линии, треугольники, квадраты и круги, не способны адекватно описать многообразие форм, встречающихся в природе. Фракталы, обладая самоподобной структурой, позволяют более точно моделировать и анализировать природные явления, открывая новые горизонты в математике и естественных науках.

Концепция фракталов была известна задолго до исследований Бенуа Мандельброта. Первой такой фигурой, которая вошла в историю как «множество Кантора», является результат работы Георга Кантора, проведенной в 1883 году. На основе этого множества математик продемонстрировал свойства самоподобия и рекурсии, которые стали основополагающими для дальнейшего изучения фрактальной геометрии.

Учёные позже выявили рекурсию в объектах живой природы, таких как деревья, молнии и облака. Структура этих объектов оказалась схожей со структурой их составляющих. Это открытие позволяет описывать природу с помощью математических законов, избегая попыток представлять её исключительно через квадратные и круглые геометрические фигуры.

Читайте также:

Рекурсия в повседневной жизни: люди, архитектура и капуста романеско

Рекурсия — это концепция, которая проявляется в различных аспектах нашей жизни. Люди, строения и даже природа демонстрируют этот феномен. В архитектуре соборов можно наблюдать рекурсивные элементы, где каждый уровень и деталь повторяют общий стиль и форму, создавая гармоничное целое. Эти конструкции не только красивы, но и символизируют сложность и глубину человеческого творчества.

Капуста романеско является ярким примером рекурсии в природе. Ее уникальная спиралевидная структура состоит из множества небольших конусов, каждый из которых напоминает общий вид растения. Это природное чудо иллюстрирует, как простые элементы могут складываться в сложные формы, отражая идею рекурсии.

Таким образом, рекурсия окружает нас повсюду, от человеческого творчества до природных форм, и помогает нам лучше понять мир, в котором мы живем.

Современные модели, основанные на фракталах, находят широкое применение в таких областях, как физика, биология, медицина и других научных дисциплинах. Ученые продолжают открывать новые закономерности, связанные с фрактальными структурами, в различных явлениях, происходящих в нашей Вселенной. Исследование фракталов помогает глубже понять сложные процессы и взаимодействия в природе, что открывает новые горизонты для научных открытий и практических приложений.

Виды фракталов

Фракталы классифицируются на три основных типа: геометрические, алгебраические и стохастические. Геометрические фракталы характеризуются самоподобием и часто встречаются в природе, например, в формах снежинок и деревьев. Алгебраические фракталы создаются с использованием математических уравнений и алгоритмов, что позволяет генерировать сложные и красивыe структуры. Стохастические фракталы, в свою очередь, основаны на вероятностных процессах и моделируют случайные явления, такие как распределение облаков или текстуры поверхности. Изучение этих типов фракталов позволяет глубже понять их свойства и применение в различных областях, включая математику, искусство и природные науки.

Геометрические фигуры формируются на основе исходной формы, которая последовательно делится и модифицируется на каждом этапе итерации. Такой подход позволяет создавать сложные структуры и узоры, основываясь на простых геометрических элементах. Использование итеративных процессов в геометрии открывает новые возможности для дизайна и анализа форм, что делает его важным инструментом в математике и искусстве.

Алгебраические конструкции основаны на алгебраических формулах. Они представляют собой важный элемент математического анализа и используются для решения различных задач в алгебре. Алгебраические выражения включают в себя переменные, константы и математические операции, что позволяет моделировать и анализировать числовые зависимости. Понимание алгебраических формул является ключевым для изучения более сложных математических концепций и применения их в практических задачах.

Стохастические процессы возникают в случае, когда в итерационной системе случайным образом изменяются один или несколько параметров. Такие изменения могут значительно влиять на поведение системы, приводя к различным результатам. Стохастические модели широко применяются в математике, статистике и экономике, позволяя анализировать системы с неопределенностью и непредсказуемыми исходами. Их использование помогает лучше понять динамику процессов и оптимизировать результаты в различных сферах, включая финансовые рынки и научные исследования.

В этом разделе мы детально рассмотрим каждый класс.

Геометрические фракталы

Фигуры, созданные на основе прямых линий, квадратов, кругов, многоугольников и многогранников, представляют собой важный аспект геометрии. В этом тексте мы рассмотрим различные примеры, начиная с самых простых форм и постепенно переходя к более сложным. Анализ этих фигур поможет лучше понять их свойства и применение в разных областях, таких как архитектура, дизайн и искусство.

В 1883 году немецкий математик Георг Кантор, основоположник теории множеств, разработал концепцию самоподобного множества. Он взял произвольный отрезок и разделил его на две равные части, затем каждую из этих частей снова разделил на две и так далее, образуя бесконечную последовательность делений. Эта идея стала основой для понимания фракталов и бесконечности в математике, а также оказала значительное влияние на развитие современных математических теорий. Канторовское множество, также известное как множество Кантора, представляет собой пример того, как можно создать сложные структуры из простых элементов, что стало важной вехой в математическом анализе и теории множеств.

Каждый шаг процесса деления прямых на две части называется итерацией. Итерации играют ключевую роль в математике и программировании, обеспечивая последовательное выполнение действий и позволяя достичь желаемого результата через повторение. Понимание итераций позволяет более эффективно решать задачи, связанные с делением, анализом данных и оптимизацией.

Итерация представляет собой процесс повторения одного и того же действия. В программировании это можно сравнить с одним прохождением цикла. На первой итерации мы имеем один отрезок, на второй — два отрезка, на третьей — четыре и так далее. Если продолжать это простое действие бесконечно и увеличить масштаб изображения, мы увидим ту же самую картину, что и в начале. Это явление иллюстрирует концепцию самоподобия, когда структура повторяется на разных масштабах. Самоподобие играет важную роль в различных областях, включая фрактальную геометрию и природу, где такие структуры можно наблюдать в растениях, облаках и других природных формах.

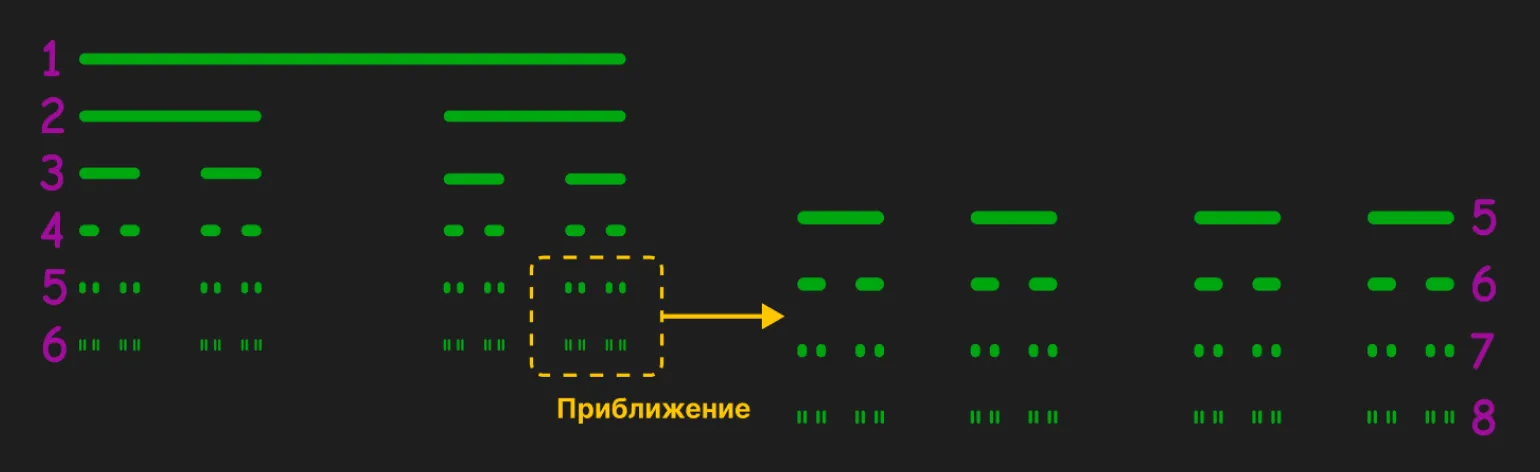
В 1904 году шведский математик Хельге Фон Кох представил свою знаменитую кривую, используя треугольник и принцип самоподобия. В результате этого исследования была создана фрактальная снежинка, которая стала классическим примером фрактальной геометрии. Кривая Фон Кох демонстрирует, как простые геометрические формы могут порождать сложные структуры, что имеет важное значение в математике и в различных областях науки. Фракталы, подобные снежинке Фон Коха, находят применение в природе, искусстве и компьютерной графике, подчеркивая красоту и сложность геометрических форм.

Представлены четыре этапа формирования фигуры. Слева находятся исходные кривые, а справа — итоговая снежинка, созданная на их основе. Ясно, что в снежинку гармонично вписываются как равносторонний треугольник, так и сама кривая. Это наглядно демонстрирует симметрию и геометрическую гармонию, присущие снежинкам, которые можно использовать в различных областях дизайна и искусства.

При увеличении масштаба изображения мы неизменно наблюдаем знакомый паттерн, аналогично множеству Кантора. Определить периметр такой снежинки невозможно, так как она продолжается бесконечно. Это является одним из ключевых свойств фракталов — их бесконечность. Фракталы представляют собой удивительные геометрические структуры, которые демонстрируют самоподобие на различных масштабах. Их изучение открывает новые горизонты в математике, физике и даже искусстве, позволяя понять, как бесконечность и сложность могут проявляться в простых формах.

Польский математик Вацлав Серпинский разработал фрактал, основываясь не только на кривых, но и на комбинации квадрата и треугольника. Его работы внесли значительный вклад в теорию фракталов и геометрию, демонстрируя, как простые геометрические формы могут создавать сложные структуры. Фракталы Серпинского являются важным примером самоподобия и находят применение в различных областях, включая компьютерную графику, физику и биологию.

Кривая Серпинского представляет собой интересный фрактал, который увеличивает своё количество копий в четыре раза с каждой итерацией. В процессе размножения фрактала его структура усложняется, создавая всё более intricate узоры. Это явление демонстрирует, как простые начальные формы могут трансформироваться в сложные геометрические конструкции, при этом сохраняя свои фрактальные свойства. Изучение кривой Серпинского помогает лучше понять основные принципы фрактальной геометрии и её применения в различных областях, таких как компьютерная графика и теоретическая математика.

Треугольник на каждом этапе делится на три равные части. Этот процесс деления позволяет создавать более мелкие треугольники, что приводит к интересным геометрическим свойствам и паттернам. При повторении этой операции можно наблюдать, как изначальная форма начинает преобразовываться, образуя фрактальные структуры. Дробление треугольника на равные части не только помогает в изучении геометрии, но и находит применение в различных областях, таких как компьютерная графика и архитектура.

Квадрат или ковёр Серпинского формируется аналогично треугольнику Серпинского, однако в этом случае исходная фигура делится на восемь квадратов. На пятой итерации становится сложно различить отдельные квадраты, так как структура начинает заполняться фрактальными узорами. Этот процесс демонстрирует, как простые геометрические формы могут создавать сложные и красивые паттерны, которые продолжают развиваться на каждой итерации. Ковёр Серпинского является ярким примером фрактальной геометрии, где повторяющиеся элементы образуют целостную картину, что делает его интересным объектом для изучения в математике и искусстве.

Геометрические фракталы могут быть созданы на основе многогранников, что позволяет им иметь объёмную структуру. Эти фракталы представляют собой сложные геометрические формы, которые обладают самоподобием на различных уровнях масштабирования. Объёмные фракталы находят применение в различных областях, включая компьютерную графику, архитектуру и искусство. Их уникальные свойства делают их интересными для изучения и создания визуально впечатляющих объектов.

Ковёр Серпинского в трёхмерном пространстве трансформируется в кубический многогранник, известный как губка Менгера. Этот фрактал представляет собой пример сложной структуры, образованной путём последовательного удаления кубов из начального объёма. Губка Менгера демонстрирует уникальные свойства самоподобия и бесконечной сложности, что делает её интересным объектом для изучения в области фрактальной геометрии. Благодаря своей необычной форме и математическим свойствам, губка Менгера находит применение в различных областях науки и искусства, включая компьютерную графику и архитектурное проектирование.

Если бы мы смогли войти в фрактал и попытались бы приблизиться к любой его стороне, то, вероятно, заблудились бы и не смогли бы выбраться, так как внутри губки Менгера скрывается бесконечное пространство. Этот принцип также можно использовать для моделирования трёхмерного треугольника Серпинского. Фракталы, такие как губка Менгера и треугольник Серпинского, демонстрируют удивительные свойства самоподобия и бесконечной сложности, что делает их интересными для изучения в математике и искусстве.

Дерево Пифагора — это рекурсивная фигура, созданная математиком Альбертом Босманом в 1942 году. Эта фигура основана на знаменитой теореме Пифагора, утверждающей, что сумма квадратов катетов равна квадрату гипотенузы. Геометрический фрактал, напоминающий дерево, демонстрирует удивительные свойства самоподобия и сложной структуры, возникающей из простых математических принципов. Дерево Пифагора служит не только примером математической красоты, но и иллюстрацией взаимодействия геометрии и природы.

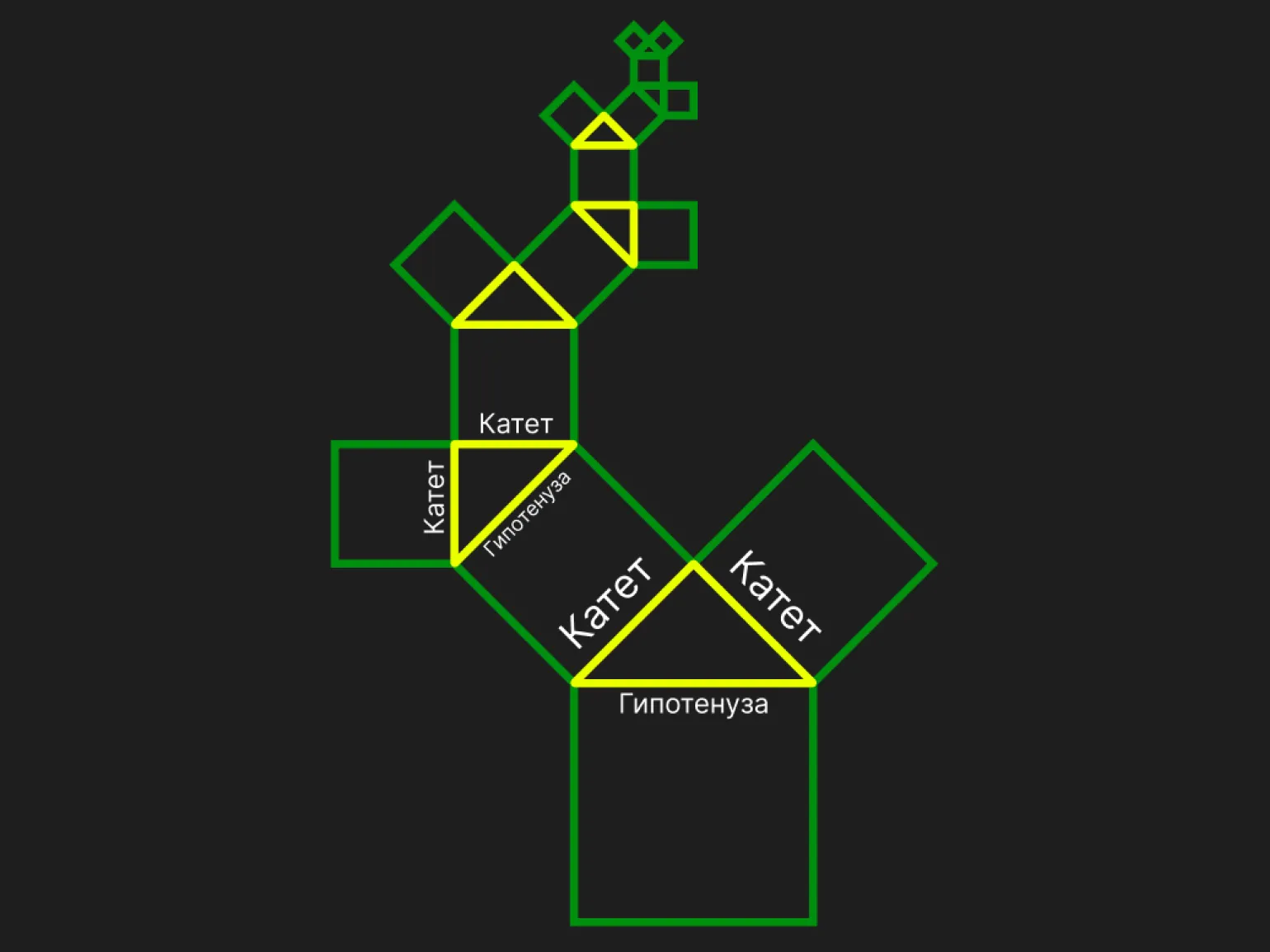
Дерево Пифагора может напомнить бинарное дерево тем, кто знаком с алгоритмами. В своей основе бинарный поиск отражает принцип Кантора, где на каждой итерации количество разветвлений удваивается. Это служит еще одной иллюстрацией концепции самоподобия, о которой уже упоминалось. Дерево Пифагора и бинарные деревья демонстрируют, как сложные структуры могут возникать из простых, повторяющихся элементов, что важно для понимания алгоритмических процессов и математических моделей.

Алгебраические фракталы

Алгебраические фракталы, в отличие от геометрических, строятся на основе математических формул вместо конкретных фигур. Они также подвержены рекурсивной итерации, что придает им уникальные и сложные формы. Алгебраические фракталы часто выглядят более причудливо и завораживающе, чем их геометрические аналоги, демонстрируя интересные свойства и закономерности, которые могут быть исследованы в математике и искусстве.

В 1905 году французский математик Пьер Фату представил концепцию множества, которое было впервые смоделировано с использованием компьютера в 1970-х годах Бенуа Мандельбротом. Это множество, известное как множество Фату, стало важным объектом изучения в области фрактальной геометрии и комплексного анализа. Его визуализация на комплексной плоскости открыла новые горизонты для исследования сложных структур и паттернов, которые возникают в математике. Множество Фату и его свойства продолжают вдохновлять исследователей и художников, демонстрируя красоту математических концепций в визуальном искусстве.

Основой данного множества является формула, которая служит ключевым элементом для его понимания и применения. Эта формула определяет структуру множества и его свойства, позволяя исследовать различные аспекты, связанные с его элементами. Правильное использование данной формулы способствует более глубокому осмыслению множества и его практического применения в различных областях, таких как математика, статистика и информатика. Понимание этой формулы является важным шагом для специалистов и студентов, стремящихся к изучению теории множеств и её практических аспектов.

Формула Zn+1 = Zn² + C описывает последовательность, используемую в комплексной динамике, которая изучает поведение итеративных функций. В этой формуле Zn представляет собой текущее значение, а C — это константа, которая влияет на форму и динамику траекторий последовательности. Данная формула является основой для создания фракталов, таких как множество Мандельброта, и находит применение в различных областях, включая математику, физику и компьютерную графику. Итерации этой функции позволяют визуализировать сложные структуры и узоры, которые возникают в результате различных значений C. Исследование таких последовательностей помогает понять динамическое поведение систем и их устойчивость.

Комплексные числа обозначаются через Z и C. Эти числа представляют собой комбинацию действительной и мнимой части, что позволяет расширить понимание числовых систем. Использование комплексных чисел находит широкое применение в различных областях математики, физики и инженерии. Понимание их свойств и операций с ними важно для изучения более сложных математических концепций. Комплексные числа играют ключевую роль в решении уравнений, анализе сигналов и векторной алгебре.

Рассмотрим комплексные числа. Важно отметить, что извлечение квадратного корня из отрицательных чисел невозможно в рамках обычной арифметики. Это объясняется тем, что квадрат любого числа, будь то положительное или отрицательное, всегда дает положительный результат. Однако именно здесь на помощь приходят комплексные числа, которые позволяют работать с квадратными корнями отрицательных значений, вводя понятие мнимой единицы, обозначаемой как i, где i^2 = -1. Таким образом, комплексные числа открывают новые возможности в математике и позволяют решать уравнения, которые в противном случае остались бы без решения.

Логика является строгой и справедливой, но исключительно в контексте действительных чисел. В общем понимании к действительным числам относятся все целые и дробные числа, включая периодические дроби, которые мы используем в повседневной жизни. Примеры таких чисел: 1, 0, -56,7, 1/3, 5/6 и многие другие. Действительные числа играют ключевую роль в математике и используются для различных вычислений и аналитических задач.

В дополнение к действительным числам в математике существует обширный класс комплексных чисел. Комплексные числа представляют собой выражения, которые имеют следующий вид:

a + bi — это общее обозначение комплексного числа, где a — это действительная часть, а b — мнимая часть, умноженная на мнимую единицу i. Комплексные числа являются важным элементом в математике, физике и инженерии, так как они позволяют описывать явления, которые не могут быть представлены только с использованием действительных чисел. В комплексных числах действительная и мнимая части могут быть использованы для решения различных уравнений и анализа сигналов. Понимание комплексных чисел и их свойств является ключевым аспектом в изучении более сложных математических концепций, таких как функции комплексного переменного и интегралы, что открывает новые горизонты в математическом анализе.

где a и b представляют собой вещественные числа. В контексте математических уравнений и функций, вещественные числа играют ключевую роль в анализе и решении различных задач. Они могут использоваться для выражения множества значений и обеспечивают непрерывность в математических моделях. Понимание свойств вещественных чисел и их применения является основой для дальнейшего изучения более сложных математических концепций.

Мнимая единица обозначается буквой i и представляет собой значение, равное √-1. В математике мнимая единица играет ключевую роль в комплексных числах, которые имеют форму a + bi, где a и b – действительные числа. Использование мнимой единицы позволяет решать уравнения, которые не имеют решения в области действительных чисел, расширяя возможности математического анализа и применения в различных областях, таких как физика и инженерия. Понимание мнимой единицы и комплексных чисел является важным аспектом в изучении алгебры и математического анализа.

Здесь происходит нарушение привычных правил арифметики.

На первый взгляд может показаться странным, что из отрицательных чисел можно извлечь квадратный корень. Многие из нас с пятого класса помнят, что это невозможно. Тем не менее, эта концепция оказалась важной в истории математики. В XVI веке она сыграла ключевую роль в решении сложных кубических уравнений. Кроме того, комплексные числа нашли широкое применение в различных областях, включая тригонометрию, что значительно расширило горизонты математических исследований и практического использования.

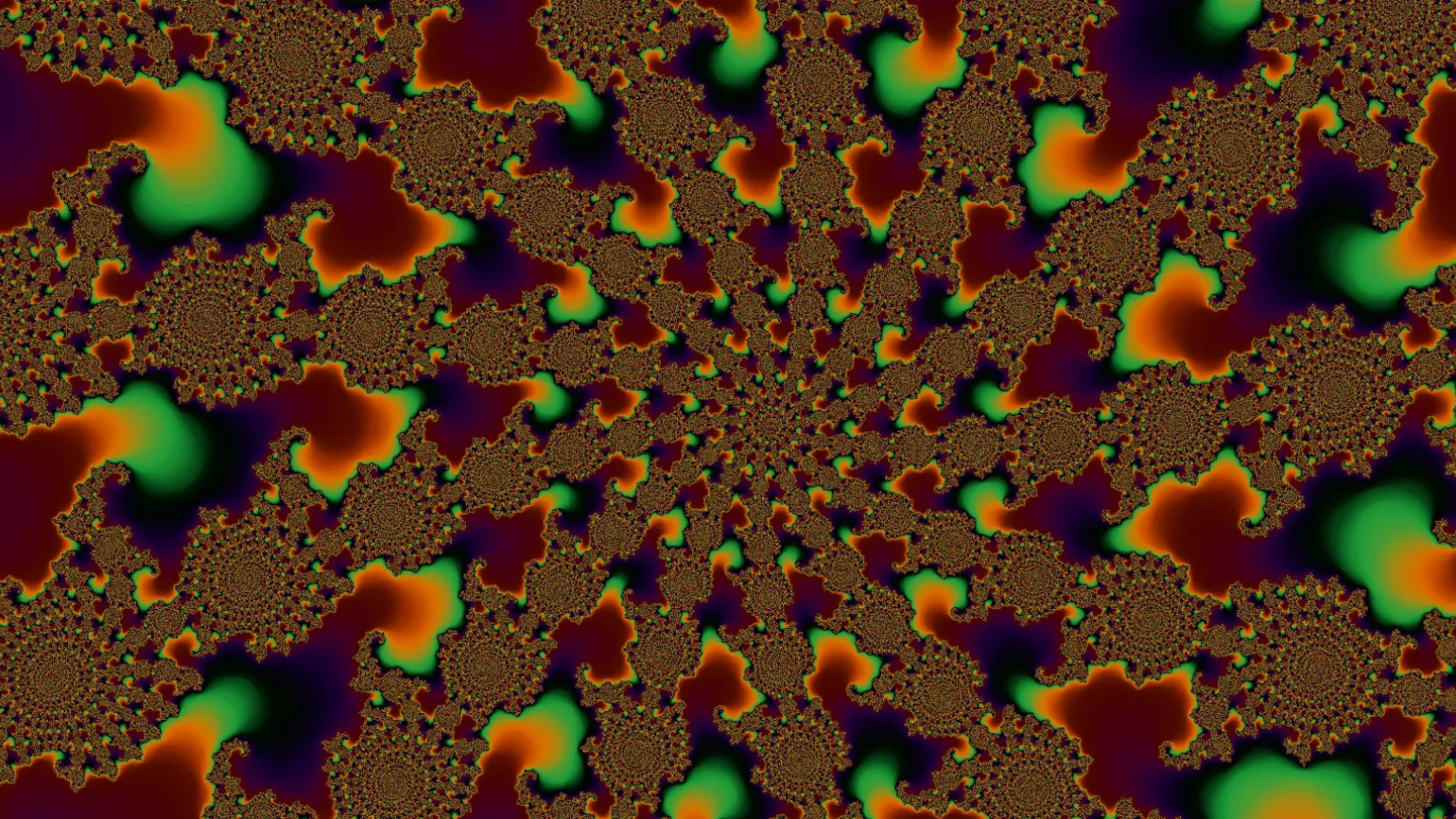
Возвращаемся к множеству Мандельброта. Предлагаем краткий обзор, чтобы освежить в памяти ключевые моменты обсуждения. Множество Мандельброта — это фрактал, обладающий уникальной геометрией и удивительными свойствами. Он возникает из сложного математического анализа и представляет собой замечательный пример взаимодействия между простыми математическими уравнениями и невероятно сложными визуальными формами. Исследование множества Мандельброта открывает двери в мир фрактальной геометрии, где каждая деталь повторяет общую структуру. Это делает его не только объектом математического интереса, но и вдохновляющим элементом для художников и дизайнеров, стремящихся к созданию уникальных визуальных работ. Важно понимать, что множество Мандельброта не просто математическая концепция, но и ключ к более глубокому пониманию сложных систем и их поведения.

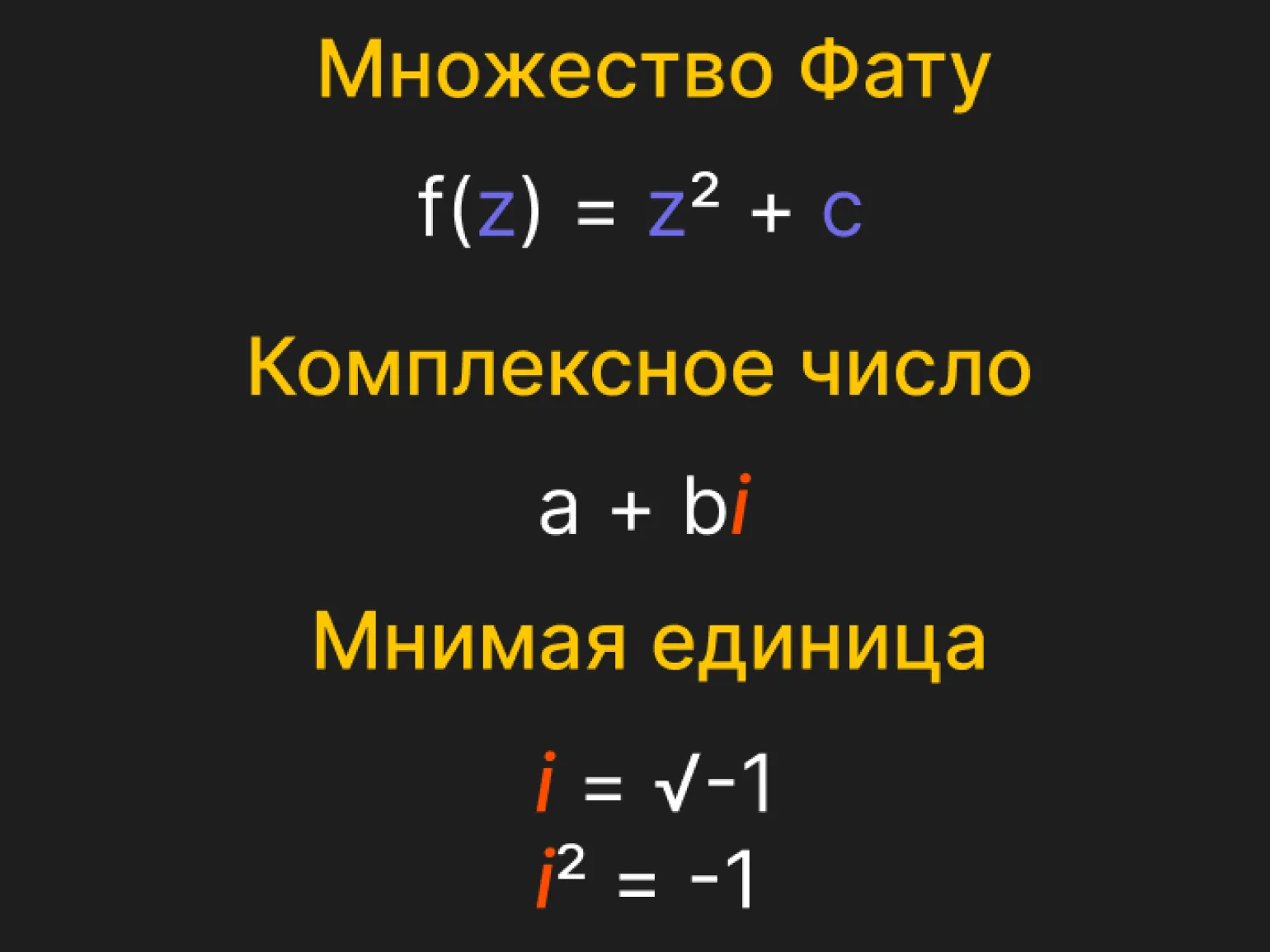
Фрактал Мандельброта основан на итеративном процессе, при котором значение функции на каждой новой итерации зависит от результата предыдущего шага. Этот подход приводит к созданию удивительных и сложных визуальных узоров, которые привлекают внимание своим разнообразием и красотой. Фрактал Мандельброта является ярким примером того, как простые математические правила могут приводить к сложным и эстетически впечатляющим изображениям.

Приближаясь к координатам множества Мандельброта, вы обнаружите бесконечные узоры, которые продолжают напоминать исходный фрактал. Изучение этих сложных форм и их повторяющихся паттернов может занять бесконечно много времени. Фракталы, подобные множеству Мандельброта, являются не только визуально впечатляющими, но и математически интересными, что делает их объектом бесконечных исследований и наблюдений.

Мы достигли лишь одной точки фрактала Мандельброта, что иллюстрирует его сложность и бесконечность. Фрактал Мандельброта представляет собой математическую конструкцию, обладающую удивительными свойствами самоподобия. Каждая точка на его поверхности может быть исследована на предмет бесконечного количества деталей и структур. Это делает фрактал не только объектом изучения в математике, но и источником вдохновения для художников, дизайнеров и создателей визуального контента. Понимание основ фракталов, таких как фрактал Мандельброта, открывает новые горизонты в различных областях науки и искусства.

Формула Zn+1 = Zn² + C описывает итеративный процесс, используемый в математике для генерации последовательностей. В данной формуле Zn обозначает текущее значение, а C — это константа, которая задает начальные условия для каждой итерации. Этот процесс находит широкое применение в теории динамических систем и фрактальной геометрии, особенно в контексте изучения множеств Мандельброта. Каждая итерация позволяет визуализировать сложные структуры, которые могут возникать из простых уравнений, что делает эту формулу важной для исследователей и художников, работающих в области компьютерной графики и математического моделирования. Эффективное использование этой формулы требует понимания начальных условий и их влияния на конечный результат.

a + bi – это стандартная форма записи комплексного числа, где a представляет действительную часть, а b – мнимую часть, умноженную на мнимую единицу i. Комплексные числа используются в различных областях математики и физики, включая электротехнику, квантовую механику и теорию сигналов. Они позволяют удобно проводить операции сложения, вычитания, умножения и деления, что значительно упрощает решение многих задач. Понимание комплексных чисел и их свойств является важным аспектом высшей математики и помогает в анализе многих математических моделей.

Множество, разработанное французским математиком Гастоном Жюлиа, основывается на формуле Фату f(z) = z² + c и напоминает фрактал Мандельброта. Однако оно имеет определенные математические отличия, которые существенно влияют на конечный результат. Эти отличия в поведении итераций функции приводят к образованию уникальных структур и узоров, что делает множество Жюлиа важным объектом изучения в области комплексного анализа и фрактальной геометрии. Изучение этих множеств помогает глубже понять природу динамических систем и их визуализацию.

Множество Мандельброта и фракталы Жюлиа являются важными объектами в мире фрактальной геометрии. Основное отличие между ними заключается в использовании параметра C. В множестве Мандельброта на каждой итерации применяется новое значение этого параметра, в то время как в фракталах Жюлиа значение C остается фиксированным на протяжении всех циклов. Это различие позволяет визуализировать фрактал Жюлиа по-разному в зависимости от выбранного значения C. Фракталы Жюлиа обладают уникальными формами и структурой, которые могут варьироваться от простых до сложных в зависимости от параметров, что делает их интересными для изучения и визуализации.

Стохастические фракталы

В отличие от геометрических и алгебраических фракталов, где формула остается неизменной, стохастические фракталы характеризуются изменением формулы на протяжении всего процесса. Эти изменения могут происходить как по определенному закону, так и случайным образом. В обоих случаях результатом являются впечатляющие визуальные эффекты, которые привлекают внимание и вдохновляют на дальнейшее исследование фрактальной геометрии. Стохастические фракталы демонстрируют удивительное разнообразие форм и структур, открывая новые горизонты в искусстве и науке.

Следующее изображение создано на основе различных фрактальных формул. Эти формулы позволяют генерировать сложные и красивые узоры, которые завораживают своей симметрией и разнообразием. Фракталы находят применение в математике, искусстве и даже в природе, где они описывают многие процессы и структуры. Использование фрактальных алгоритмов для создания изображений открывает новые горизонты в визуализации данных и художественном выражении.

Ученые используют сложные стохастические законы для воспроизведения структур объектов живой природы. Внося отклонения на различных итерациях в такие фракталы, как дерево Пифагора или снежинка Коха, можно создать изображения наклоненной листвы или генерировать бесконечное количество уникальных снежинок. Этот подход открывает новые горизонты в понимании природных форм и позволяет моделировать их разнообразие с высокой степенью реалистичности.

Фрактальная графика

Принцип самоподобия является основой для целого направления в компьютерной графике. Этот метод позволяет компьютерам хранить не готовые объекты, а только формулы для их отрисовки, что существенно экономит память и ресурсы. Использование самоподобия в графике открывает новые возможности для создания сложных и детализированных изображений, позволяя эффективно управлять данными и производительностью. Такой подход широко применяется в фрактальной графике, моделировании природных явлений и в других областях, где требуется высокая степень детализации при минимальных затратах памяти.

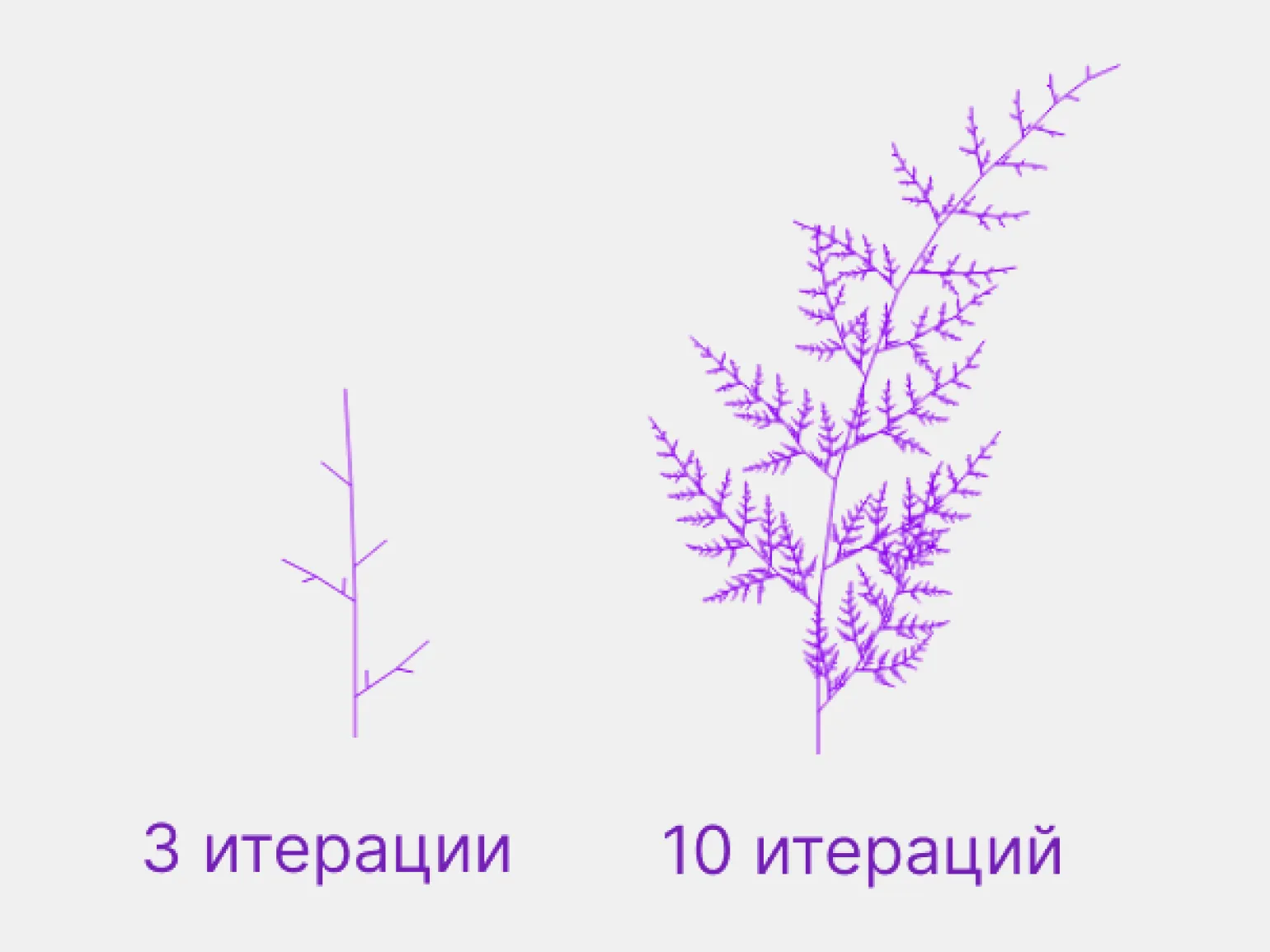
Появляется возможность создания как конкретных объектов, так и абстрактных 3D-моделей, описывая лишь часть конечного изображения. Например, можно сгенерировать известный папоротник Барнсли, задав формулу для построения одной ветви, указав количество итераций и добавив случайные изменения на последующих этапах. Такой подход позволяет эффективно использовать математические алгоритмы для визуализации сложных форм и текстур, что открывает новые горизонты в графическом дизайне и 3D-моделировании.

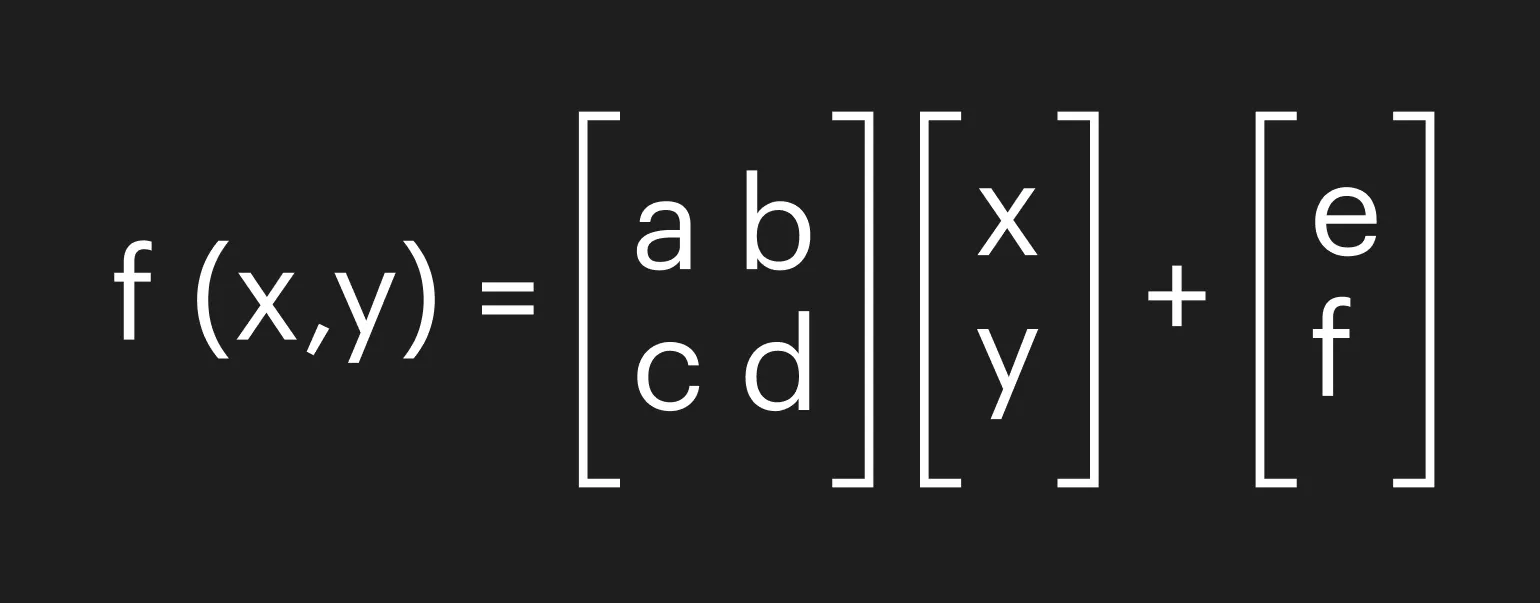
Фракталы в физике

Принципы фракталов находят применение в различных областях физики, таких как гидродинамика, физика плазмы, электродинамика и радиоэлектроника. Одним из наиболее значительных изобретений в этой сфере является фрактальная антенна, созданная американским инженером Натаном Коэном в 1995 году. Эта антенна отличается компактными размерами и высокой эффективностью, что позволяет использовать ее в современных коммуникационных системах. Фрактальные структуры обеспечивают улучшенные характеристики передачи и приема сигналов, что делает их актуальными для применения в мобильной связи и беспроводных технологиях.

Главное преимущество данной антенны заключается в её широком диапазоне рабочих частот, что делает её универсальным решением для различных приложений. Кроме того, она имеет компактные размеры по сравнению с классическими антеннами, что позволяет значительно экономить пространство. Эта антенна также может использоваться в качестве основы для подводных антенн, что расширяет её функциональные возможности и области применения.

Конструкция Коэна схожа с фракталом Коха, известным своей симметрией и сложностью. Оба этих объекта представляют собой примеры фрактальной геометрии, демонстрируя, как простые правила могут создавать сложные и красивые структуры. Фракталы, такие как снежинка Коха, иллюстрируют, как можно повторять процесс деления и модификации, чтобы получить новые формы. В этом контексте конструкция Коэна также служит отличным примером применения фрактальных принципов в математике и искусстве. Изучение таких конструкций помогает лучше понять природу фракталов и их влияние на современную науку и дизайн.

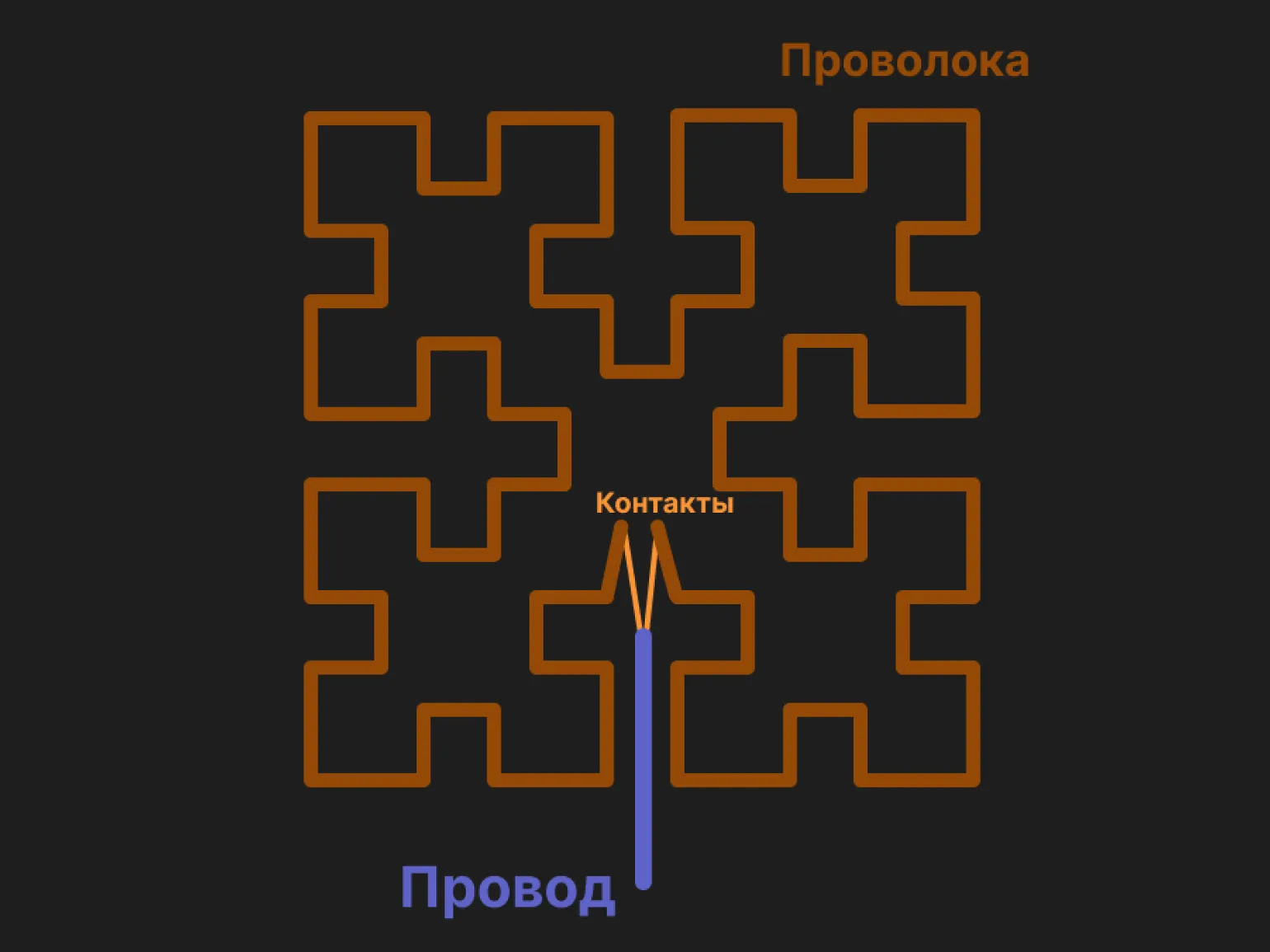
В начале 2000-х годов антенны размером 30 × 40 мм начали активно применяться в мобильных устройствах. Позже инженеры разработали антенны, основанные на фракталах Серпинского, кривых Пеано и фрактале Коха. Эти инновационные подходы позволили значительно улучшить характеристики связи и уменьшить размеры антенных систем, что стало важным шагом в развитии мобильной связи и беспроводных технологий. Использование фрактальных структур в дизайне антенн открывает новые возможности для повышения их эффективности и универсальности в современных устройствах.

Фракталы в природе

Стохастические фракталы представляют собой инновационный подход к описанию природных объектов и явлений. Этот метод объясняет, как горы, облака, молнии, реки, растения, клетки живых организмов и даже галактики обладают общим свойством самоподобия. Фрактальная геометрия позволяет глубже понять структуру и динамику окружающего мира, выявляя закономерности, которые ранее оставались незамеченными. Благодаря этому подходу ученые могут проводить более точный анализ природных процессов и предсказывать их поведение.

Капуста Романеско — один из самых красивых фракталов в природе. Этот уникальный овощ привлекает внимание своей спиральной формой и ярким зеленым цветом. Фрактальный узор капусты Романеско можно наблюдать в каждом ее соцветии, что делает ее не только вкусным, но и эстетически привлекательным продуктом. Употребление Романеско в пищу приносит пользу благодаря высокому содержанию витаминов и минералов. Этот овощ часто используется в кулинарии для создания оригинальных и полезных блюд, а также как элемент декора. Капуста Романеско — отличный выбор для тех, кто ценит не только вкус, но и визуальную привлекательность пищи.

Фракталы окружают нас повсеместно, и их можно наблюдать в повседневной жизни. Достаточно просто выйти на улицу и обратить внимание на природу. Примером служит дерево Пифагора, название которого связано с его ярким отражением принципа самоподобия. Ветви деревьев образуют структуры, которые повторяются на разных масштабах, демонстрируя удивительные геометрические формы, характерные для фракталов. Эти природные образования не только красивы, но и служат важными иллюстрациями математических концепций, которые могут быть применены в различных областях науки и искусства.

Существует множество примеров стохастических фракталов, которые можно наблюдать в листьях и растениях. Эти фрактальные структуры проявляются в различных формах и размерах, создавая уникальные узоры, характерные для каждого вида. Например, ветвление листьев и расположение жилок часто демонстрируют фрактальную симметрию, что позволяет растениям эффективно использовать солнечный свет и воду. Стохастические фракталы также можно заметить в форме цветков, где каждая отдельная часть растения, от лепестков до семян, следует определённым математическим закономерностям. Изучение этих явлений не только углубляет наши знания о растительном мире, но и помогает в разработке новых технологий, таких как биомиметические материалы и устойчивые архитектурные решения.

Вместо вывода: применение фракталов в жизни

Сегодня фракталы находят применение в различных сферах, включая математику, искусство и науку. Эти удивительные геометрические структуры показывают, как сложные формы могут возникать из простых правил. В математике фракталы используются для моделирования природных явлений, таких как облака и горные пики. В искусстве фракталы вдохновляют художников создавать уникальные произведения, которые завораживают своей симметрией и сложностью. Также фракталы применяются в компьютерной графике для создания реалистичных текстур и анимаций. Их свойства позволяют эффективно обрабатывать и сжимать изображения, что делает их важным инструментом в цифровом мире. Фракталы продолжают открывать новые горизонты в исследовании и понимании окружающей нас реальности.

• С их помощью описывают различные явления классической механики, гидродинамики, электродинамики и геофизики.
• В телекоммуникациях они позволяют моделировать электромагнитные поля в сотовой и спутниковой связи.
• В биологии — точно описывать структуру природных объектов, моделировать и предсказывать их поведение.
• Медицина использует фракталы для исследования внутренних процессов в организме человека, изучения сердечного ритма, работы кровеносных сосудов и нервной системы.
• В экономике на основе фракталов проводят анализ рынков и выявляют закономерности в поведении цен.
• В трёхмерной графике их используют для создания сложных текстур и моделей, таких как деревья, облака и морские волны.
• В искусстве и дизайне — когда нужно создать нестандартную «психоделическую» композицию, погрузить зрителя в новые измерения.

Фракталы представляют собой лишь один из множества способов применения в различных областях. Исследование фракталов — это относительно новая ветвь математики, и на сегодняшний день продолжаются новые открытия и разработки. Выявление закономерностей и особенностей фракталов открывает новые горизонты в науке и искусстве, что делает их изучение актуальным и важным.

Узнайте больше о кодировании и программировании, подписавшись на наш телеграм-канал. Мы регулярно делимся полезной информацией, советами и интересными фактами о разработке. Присоединяйтесь к сообществу, чтобы быть в курсе последних новостей и тенденций в мире технологий.

Читайте также:

• Интегралы: всё, что вы хотели знать, без интриг и сложных терминов
• Тест: насколько хорошо ты знаешь устройство процессора?
• Хакеры: кто они, какие бывают и при чём тут шляпы