Какие числа являются рациональными: свойства, примеры, определения / Skillbox Media

Содержание:

• Что такое рациональные числа
• Чем рациональные числа отличаются от остальных
• Свойства рациональных чисел
• Рациональные числа в Python
• Резюме: повторим изученное

Числа действительно играют ключевую роль в нашей жизни, как утверждал Пифагор. Однако важно понимать, какие именно числа мы используем в разных ситуациях. Например, натуральные числа не подходят для описания отрицательного баланса на банковской карте или для точного значения скорости света. В таких случаях необходимы более сложные математические инструменты, такие как рациональные числа. Рациональные числа позволяют нам работать с дробями и отрицательными значениями, что делает их незаменимыми в различных областях науки и повседневной жизни. Таким образом, для точного описания реальности важно выбирать правильные числовые системы.

Сегодня мы рассмотрим, что собой представляют рациональные числа, их назначение и происхождение. Этот материал будет полезен не только студентам, готовящимся к экзаменам, но и новичкам в сфере информационных технологий. В завершение статьи мы обсудим, как работать с рациональными числами на языке Python.

В данной статье вы познакомитесь с основными аспектами и ключевыми моментами, которые помогут вам лучше понять тему. Мы рассмотрим важные детали, предоставим полезные советы и рекомендации, а также ответим на часто задаваемые вопросы. Эта информация будет полезна как новичкам, так и тем, кто уже имеет опыт в данной области. Читайте далее, чтобы углубить свои знания и получить практические навыки.

• что такое рациональные числа;
• чем они отличаются от остальных;
• какие у них есть свойства;
• как работать с рациональными числами в Python;
• резюме: что нужно запомнить.

Что такое рациональные числа

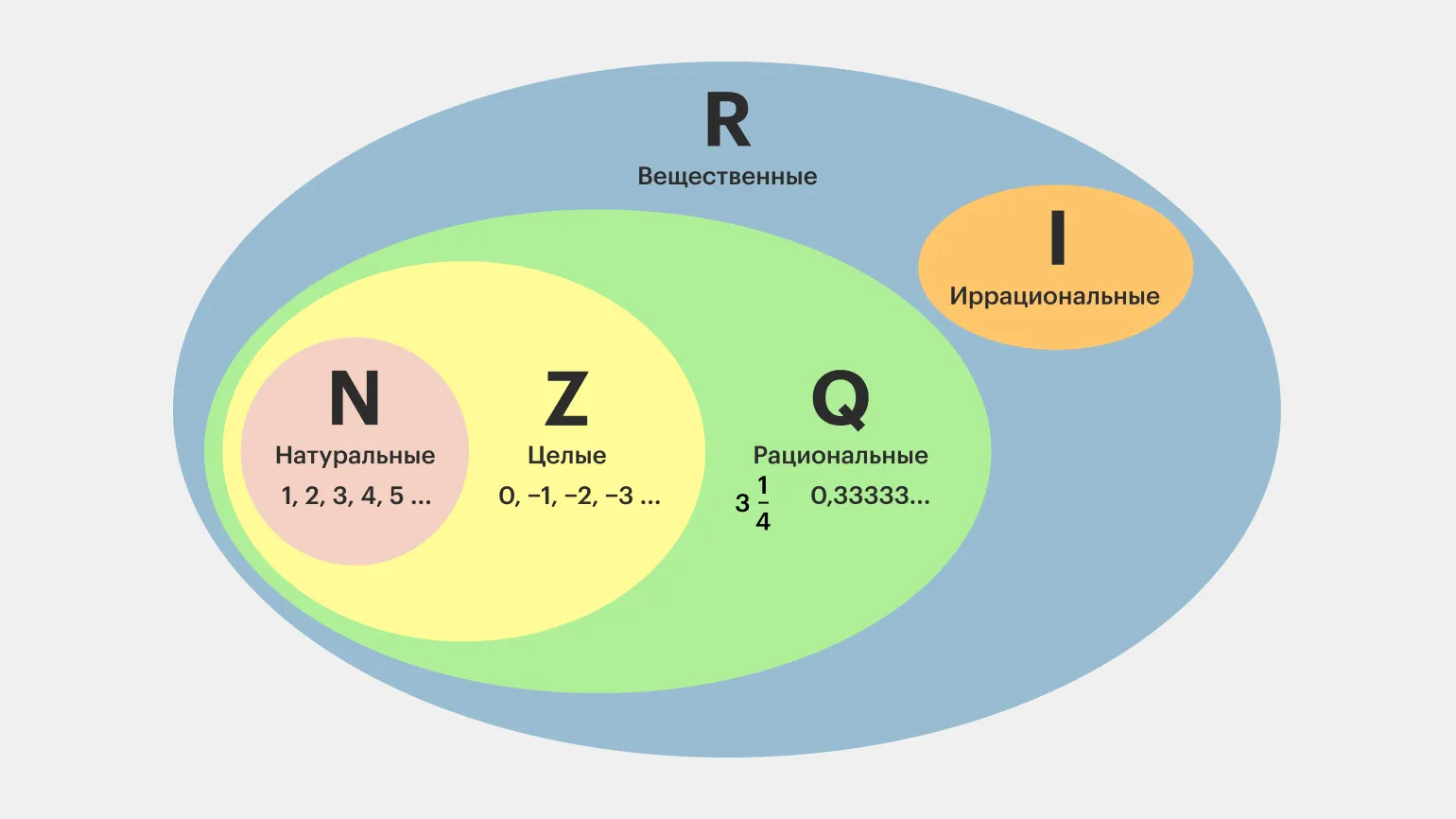
Рациональные числа — это числа, которые могут быть выражены в виде дроби m/n, где m является целым числом, а n — натуральным числом. Множество рациональных чисел обозначается латинской буквой Q. Эти числа включают как положительные, так и отрицательные значения, а также ноль. Рациональные числа играют важную роль в математике и повседневной жизни, так как они позволяют выполнять различные арифметические операции и представляют собой основу для более сложных чисел, таких как действительные и комплексные числа.

Число 0,5 можно выразить в виде дроби, например, 5/10 или ½, что подтверждает его принадлежность к классу рациональных чисел. В математической нотации это обозначается как 0,5 ∈ Q. Рациональные числа включают в себя все числа, которые могут быть представлены в виде дроби, где числитель и знаменатель являются целыми числами, а знаменатель не равен нулю.

Любое целое число можно отнести к категории рациональных чисел, поскольку его можно представить в виде дроби. Например, число 5 можно записать как 5/1. В этом случае оно не отличается от деления 5 на 1, что также приводит к тому же результату — пятёрке. Таким образом, все целые числа являются рациональными числами, так как их можно выразить в форме дроби, где числитель и знаменатель — это целые числа, а знаменатель не равен нулю.

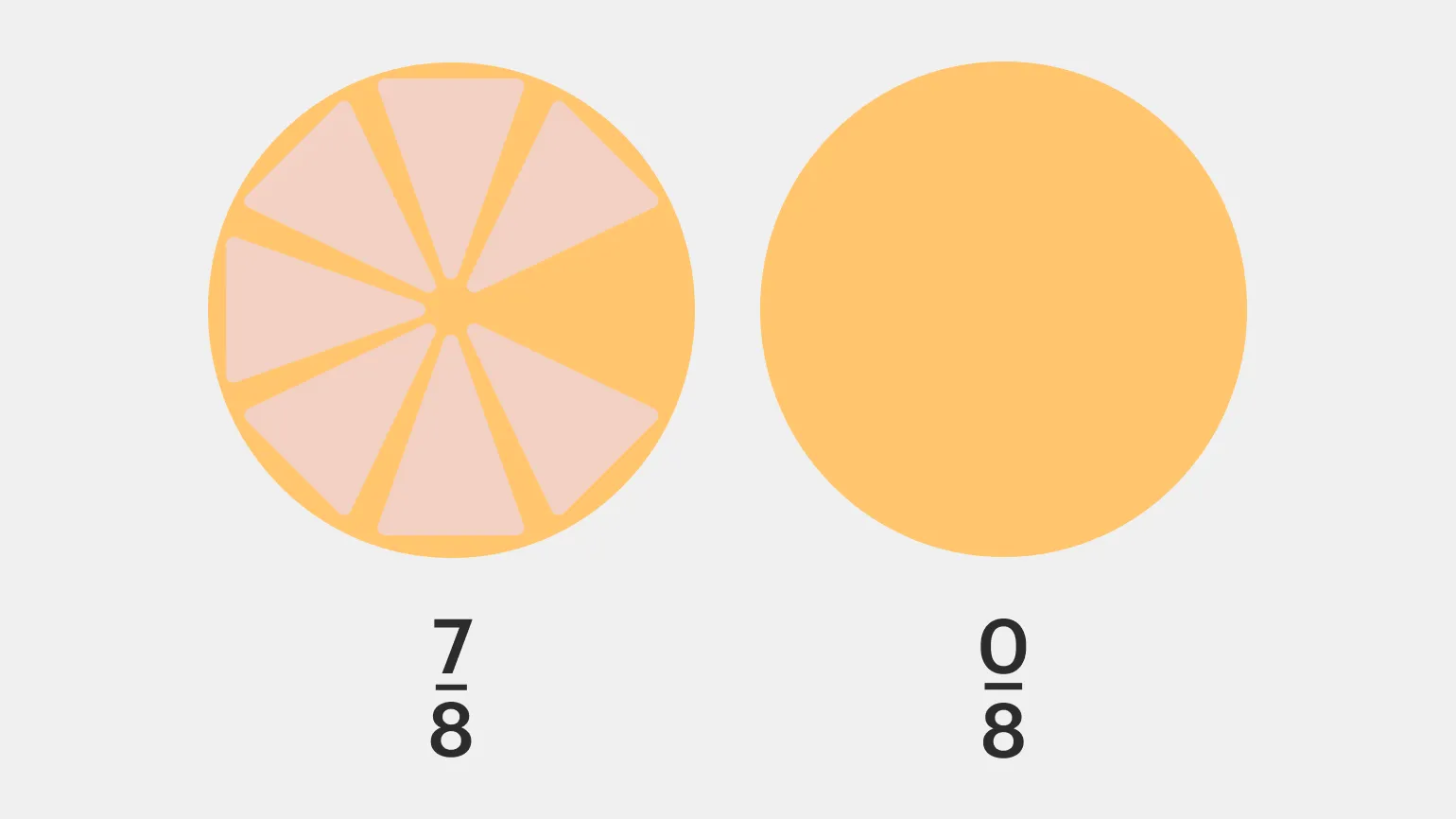
Ноль считается рациональным числом, поскольку его можно выразить в виде дроби. Однако деление на ноль является математически некорректным, поэтому знаменатель в дроби, представляющей ноль, должен быть не меньше единицы. Для наглядности рассмотрим следующий пример: если у нас есть 7 из 8 кусочков пиццы, это можно записать как дробь 7/8. После того как все кусочки будут съедены, у нас останется 0 из 8, что соответствует дроби 0/8. Этот пример показывает, как ноль вписывается в концепцию рациональных чисел и иллюстрирует его значение в математике.

Бесконечные периодические дроби являются частью рациональных чисел. Рассмотрим дробь 1/7. При делении 1 на 7 мы получаем 0,14285714285714…, где последовательность 142857 повторяется бесконечно. Это означает, что 1/7 можно выразить как периодическую дробь. Обратное преобразование, возвращающее нас к дроби 1/7, подтверждает, что такие числа принадлежат рациональному множеству. Таким образом, бесконечные периодические дроби играют важную роль в теории чисел и являются примером рациональных чисел в математике.

Если после запятой у дроби отсутствует повторяющаяся последовательность, такое число считается иррациональным. Примером иррационального числа является √2, которое приближенно равно 1,41421356237… Другим известным примером является число π (пи), равное приблизительно 3,1415926535… Иррациональные числа играют важную роль в математике и используются в различных областях, включая геометрию, физику и инженерные науки. Их уникальные свойства делают их интересными для изучения и применения в научных исследованиях.

Рациональные числа представляют собой числа, которые могут быть представлены в виде дроби, где числитель и знаменатель — это целые числа, а знаменатель не равен нулю. К примеру, числа 1/2, -3/4 и 7 являются рациональными. Любое целое число можно рассматривать как рациональное, если его представить в виде дроби со знаменателем 1. Также к рациональным числам относятся такие числа, как 0.75 и -2.5, которые можно выразить в виде дробей 3/4 и -5/2 соответственно. Важно отметить, что рациональные числа могут быть как положительными, так и отрицательными, и они имеют бесконечное количество десятичных знаков, если представляются в десятичной форме, но всегда заканчиваются или начинают повторяться. Рациональные числа играют важную роль в математике и используются в различных областях, таких как экономика, физика и инженерия.

• Целое положительное натуральное число 1 — это 1/1.
• Целое число 0 — это 0/1.
• Целое отрицательное число −5 — это −5/1.
• Десятичная дробь 0,25 — это 25/100.
• Отрицательная десятичная дробь −0,75 — это −75/100.
• Смешанное число 3,25 — это 13/4.
• Бесконечная периодическая дробь 0,333… — это 1/3.

Чем рациональные числа отличаются от остальных

Рациональные числа — это важная категория чисел в математике, которую стоит подробно рассмотреть. Рациональное число представляет собой отношение двух целых чисел, где делитель не равен нулю. Это значит, что любое рациональное число можно записать в виде дроби, например, 1/2 или -3/4.

Рациональные числа включают в себя как положительные, так и отрицательные значения, а также ноль. Они образуют множество, которое обозначается символом Q. Важно отметить, что рациональные числа могут быть представлены как конечные или периодические десятичные дроби. Например, 0.25 — это конечная дробь, а 0.333… — периодическая.

Понимание рациональных чисел является основой для изучения более сложных математических концепций, таких как иррациональные числа, действительные числа и комплексные числа. Эти числа играют ключевую роль в различных областях математики и ее приложениях в реальной жизни. Знание о рациональных числах поможет вам лучше ориентироваться в математике и использовать их в практических задачах.

Натуральные числа представляют собой все положительные целые числа, начиная с 1 и продолжающиеся до бесконечности. Важно отметить, что ноль не включается в этот набор. Натуральные числа находят широкое применение в повседневной жизни для учета материальных объектов, таких как одна монета, два фломастера или пять автомобилей. Этот тип чисел является одним из самых древних, и его использовали для расчетов еще в эпоху первобытного общества. Натуральные числа служат основой для более сложных математических концепций и остаются актуальными в различных сферах, включая экономику, статистику и науку.

Целые числа включают все натуральные числа, их отрицательные counterparts и ноль. Исторически сложилось, что использование целых чисел началось в Древнем Китае и Древней Индии, где они применялись для обозначения долгов и расчетов. Целые числа играют важную роль в математике, они используются в различных областях — от арифметики до алгебры и теории чисел. Понимание целых чисел и их свойств является основой для изучения более сложных математических концепций.

Рациональные числа представляют собой множество, включающее натуральные и целые числа, а также дроби. Дроби могут быть обыкновенными, конечными десятичными и бесконечными периодическими. Периодическими называются дроби, в которых одна или несколько цифр после запятой повторяются, например, 0,161616… Если же такая периодичность отсутствует, число классифицируется как иррациональное. Рациональные числа играют ключевую роль в математике и используются в различных областях, включая экономику, физику и инженерные науки.

Иррациональные и рациональные числа формируют новое множество — вещественные числа. Это множество включает в себя все числа, которые могут быть представлены на числовой прямой. Рациональные числа могут быть выражены в виде дроби, где числитель и знаменатель являются целыми числами, а иррациональные числа не могут быть представлены в таком виде. Примеры иррациональных чисел включают квадратный корень из 2 и число π. Вещественные числа играют ключевую роль в математике и других науках, так как они используются для описания непрерывных величин и представляют собой основу для анализа и моделирования различных процессов.

Свойства рациональных чисел

Рациональные числа, как и другие математические объекты, обладают определенными свойствами. В приведенных ниже примерах a, b и c обозначают рациональные числа. Эти свойства играют важную роль в различных математических операциях и теоремах. Понимание свойств рациональных чисел помогает в решении математических задач и в изучении более сложных концепций.

Переместительное свойство утверждает, что сумма не изменяется при перестановке слагаемых. Это основное свойство арифметики, которое позволяет нам уверенно манипулировать числами. Независимо от порядка, в котором мы складываем числа, итоговая сумма всегда останется одинаковой. Это свойство является фундаментальным для более сложных математических операций и упрощает вычисления в различных задачах. Правильное понимание переместительного свойства важно для успешного изучения математики и ее применения в реальной жизни.

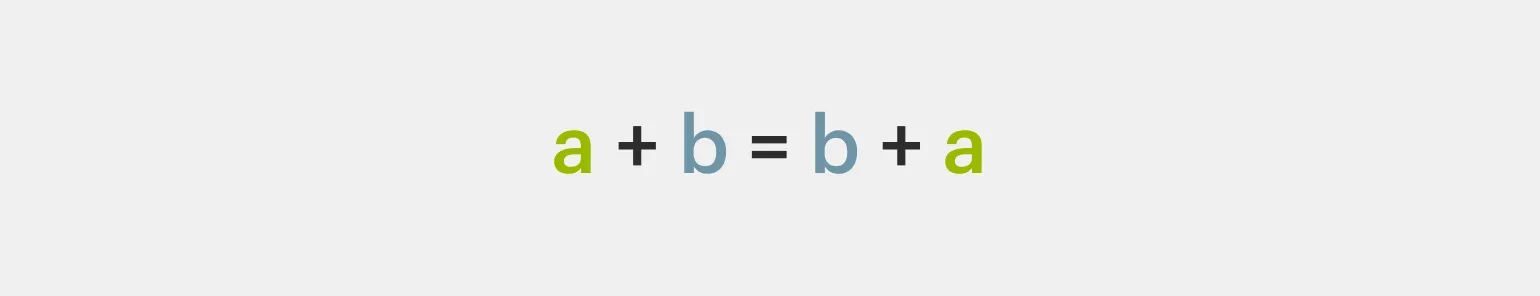
Сочетательное свойство утверждает, что для прибавления к рациональному числу суммы двух других чисел, необходимо сначала к этому числу добавить одно из слагаемых, а затем прибавить второе слагаемое. Это свойство является основополагающим в арифметике и позволяет упростить вычисления, обеспечивая гибкость в порядке операций. Важно помнить, что применение сочетательного свойства помогает избежать ошибок и ускоряет процесс решения математических задач.

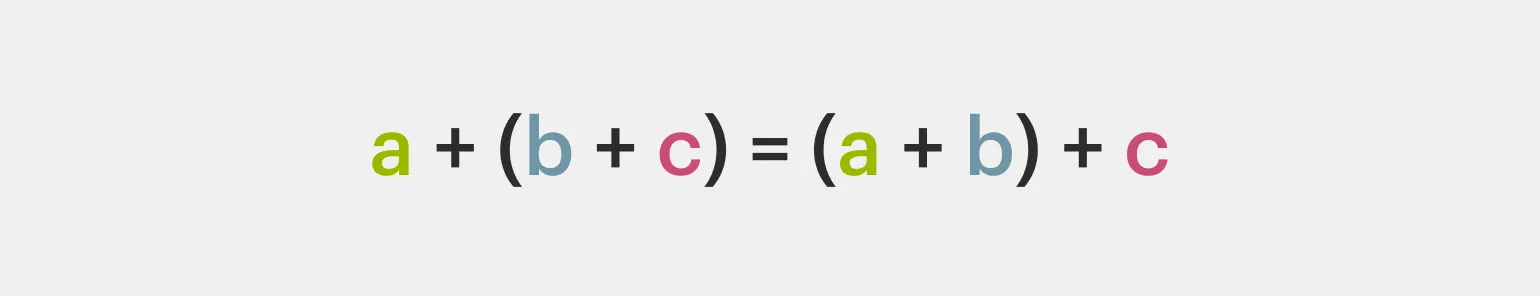
Ноль является нейтральным элементом в арифметических операциях. При сложении нуля с любым рациональным числом результат остается неизменным. Это свойство делает ноль важным элементом в математике, позволяющим сохранять значение чисел при выполнении операций.

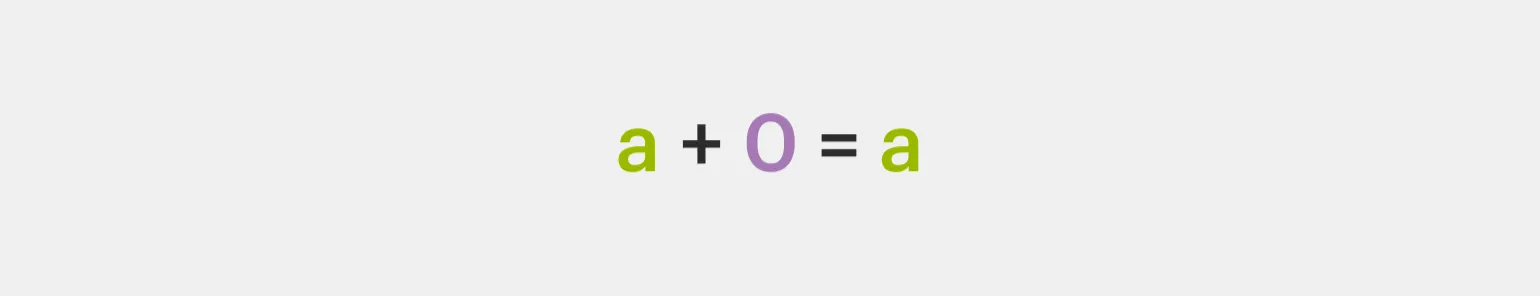
Каждое рациональное число имеет свое противоположное значение. При сложении рационального числа и его противоположного мы получаем ноль. Это свойство играет важную роль в математике, так как ноль является нейтральным элементом для операции сложения. Противоположные числа помогают лучше понять структуру чисел и их взаимосвязи.

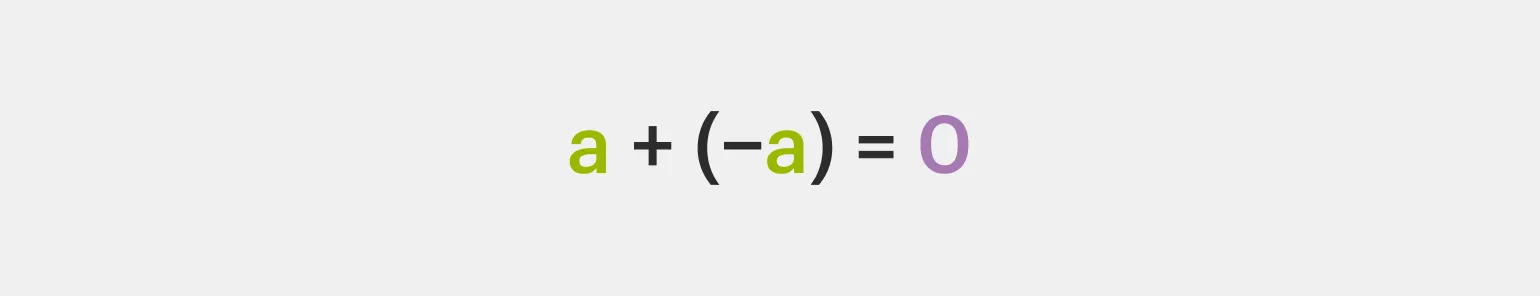
Для лучшего запоминания этих свойств воспользуйтесь следующей шпаргалкой. Эта памятка поможет вам быстро восстановить в памяти ключевые характеристики и особенности, что сделает изучение материала более эффективным. Используйте шпаргалку как инструмент для повторения и закрепления знаний, что поможет вам лучше ориентироваться в теме и повысит уровень вашей подготовки.

Здесь всё практически аналогично.

Переместительное свойство гласит, что при умножении множителей их порядок не влияет на результат. Это означает, что можно менять местами множители, и произведение останется неизменным. Например, если мы умножаем 2 на 3, результат будет равен 6, так же как и при умножении 3 на 2. Это свойство является основополагающим в арифметике и помогает упростить расчетные операции. Понимание переместительного свойства способствует более глубокому усвоению математических концепций и улучшению навыков в решении задач.

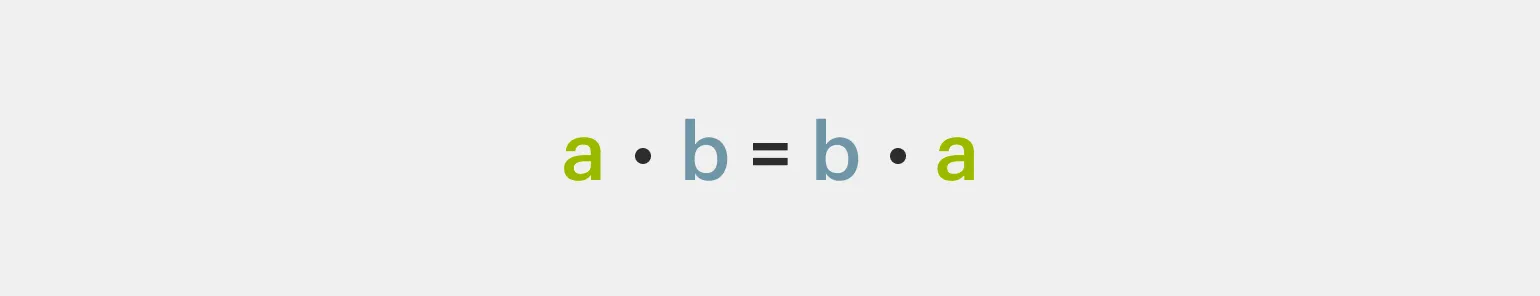
Сочетательное свойство умножения утверждает, что для умножения рационального числа на произведение двух множителей достаточно сначала умножить это число на первый множитель, а затем полученный результат умножить на второй множитель. Это свойство позволяет упростить вычисления и лучше организовать процесс умножения в математике.

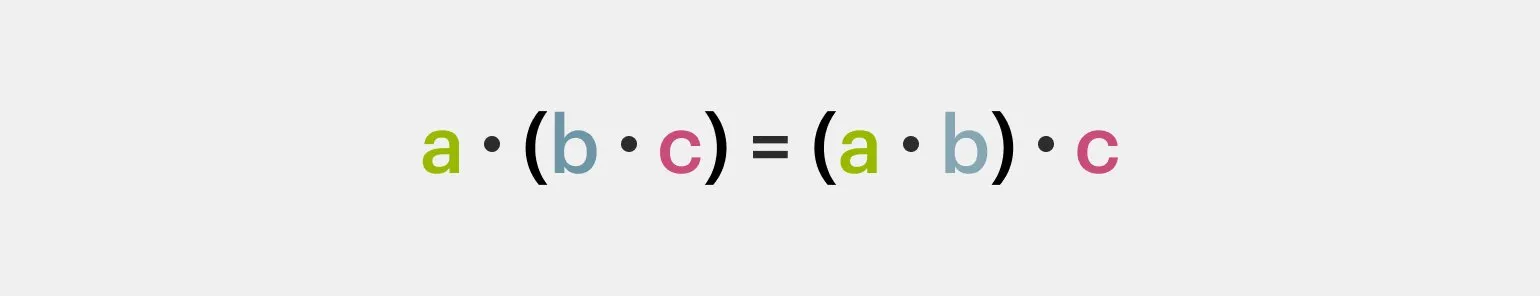
Свойство умножения на 1. Умножая рациональное число на 1, мы сохраняем его значение. Это свойство является основополагающим в математике, поскольку показывает, что 1 является нейтральным элементом для операции умножения. Например, если мы умножим число 5 на 1, результатом будет 5. Это правило применимо для всех рациональных чисел, включая дроби и отрицательные значения. Понимание этого свойства помогает в решении различных математических задач и упрощает вычисления.

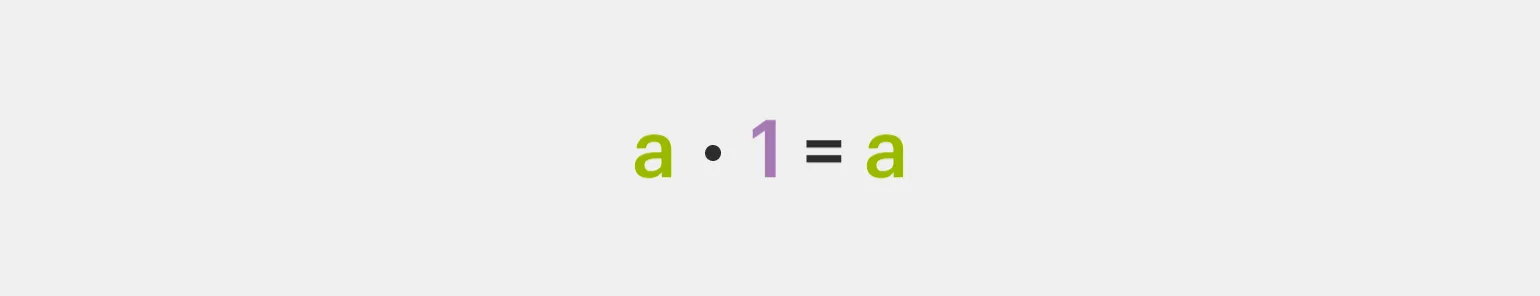
Свойство умножения на ноль гласит, что любое рациональное число, умноженное на ноль, всегда равно нулю. Это базовое математическое правило, которое применяется в различных областях математики и науки. Независимо от значения множителя, результат умножения на ноль остается неизменным и равен нулю. Это свойство важно учитывать при решении уравнений и упрощении математических выражений.

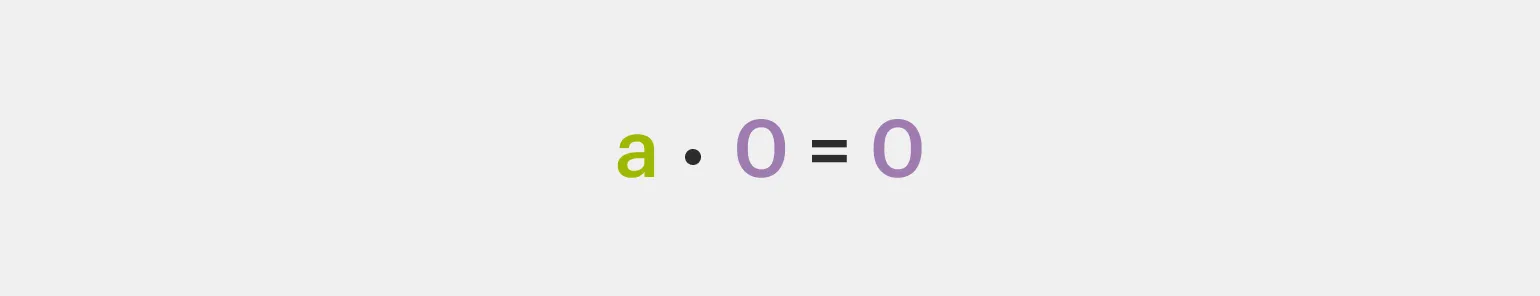
Свойство умножения на дробь. При умножении рационального числа на дробь, где в числителе находится 1, а в знаменателе – это же рациональное число, результатом будет 1. Данное свойство иллюстрирует основную концепцию обратных величин в математике и подчеркивает важность дробей в расчетах. Умножение на дробь позволяет упростить многие математические задачи и является основополагающим элементом в изучении алгебры и рациональных выражений.

Распределительное свойство гласит, что при умножении суммы на рациональное число можно умножить это число на каждое слагаемое отдельно, а затем сложить полученные результаты. Это правило также применимо к вычитанию. Таким образом, если у вас есть выражение, например, a + b, и вы умножаете его на число c, вы можете представить это как c * (a + b) = c * a + c * b. Аналогичным образом, для вычитания: c * (a — b) = c * a — c * b. Распределительное свойство является важным инструментом в алгебре, позволяющим упрощать вычисления и решать уравнения более эффективно.

Умножение чисел с разными знаками имеет свои особенности. Если в операции участвует хотя бы одно отрицательное число, то результат произведения всегда будет отрицательным. Это правило основано на том, что умножение положительного числа на отрицательное дает отрицательное значение, а также умножение отрицательного числа на положительное также приводит к отрицательному результату. Таким образом, важно помнить, что при умножении чисел с разными знаками итоговое значение всегда будет отрицательным.

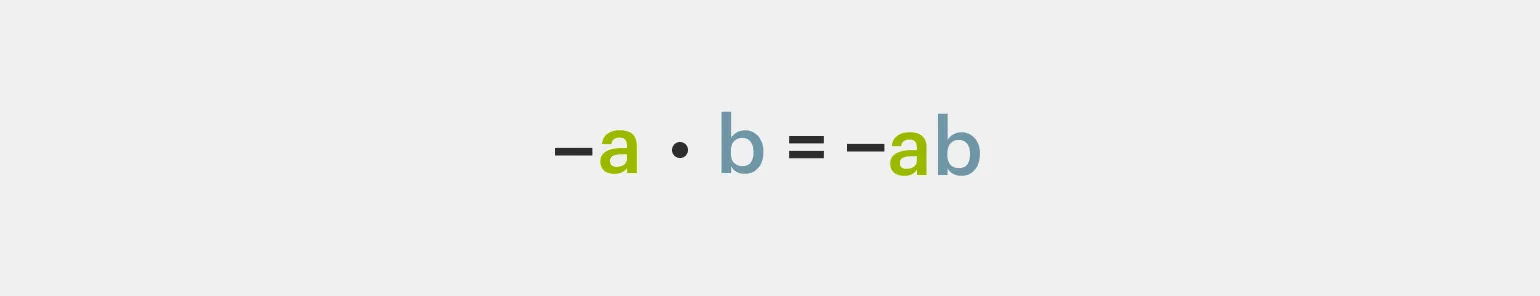
Умножение отрицательных чисел имеет важное значение в математике. Когда мы умножаем два отрицательных числа, результат всегда будет положительным. Это объясняется тем, что умножение отрицательного числа на другое отрицательное число приводит к отмене негативного знака. Таким образом, минус на минус дает плюс. Понимание этой концепции является основой для работы с числами в различных математических задачах и уравнениях.

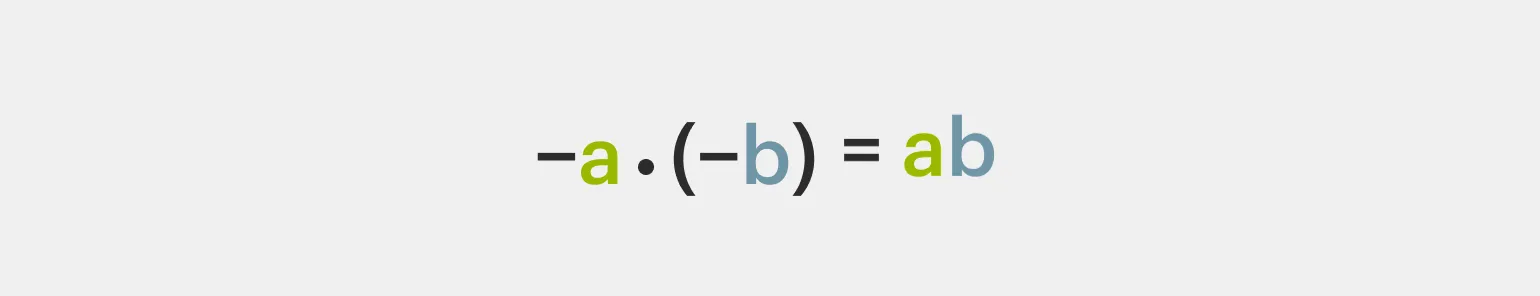
Свойства вычитания рациональных чисел можно объяснить аналогично свойствам сложения, однако важно правильно учитывать знаки. Например, вычитание можно представить в виде: a − b = −b + a. Эта формула подчеркивает, что вычитание можно преобразовать в сложение с отрицательным числом, что значительно упрощает выполнение операций с рациональными числами. Правильное понимание свойств вычитания поможет избежать ошибок и улучшит навыки работы с числами в математике.

Свойства деления рациональных чисел противоположны свойствам умножения. Это означает, что операции деления имеют свои уникальные правила и особенности, которые важно учитывать при работе с рациональными числами. Например, деление на ноль невозможно и приводит к неопределенности, в то время как умножение на ноль всегда дает ноль. Кроме того, деление рациональных чисел также подчиняется правилам, связанным с делением положительных и отрицательных чисел, что влияет на знак результата. Понимание этих свойств является ключевым моментом в математике, особенно при решении задач, связанных с дробями и рациональными выражениями.

Рациональные числа в Python

В этой статье мы рассмотрим понятие рациональных чисел и их свойства с использованием языка программирования Python. В Python существует специальный модуль fractions, который облегчает работу с рациональными числами. В этом модуле реализован класс Fraction, который позволяет эффективно представлять дробные значения и выполнять с ними различные арифметические операции. Использование данного класса обеспечивает точность расчетов и упрощает работу с дробями в программах.

Начнем с импорта класса Fraction из модуля fractions, который позволит нам работать с дробями. Это даст нам возможность выполнять различные математические операции с дробными числами, обеспечивая точность и удобство в расчетах. Импортировав класс, мы сможем легко создавать объекты дробей и использовать их в дальнейших вычислениях.

Теперь рассмотрим работу класса Fraction. При создании объекта этого класса в конструктор можно передать значения, которые определяют дробь. Это позволяет удобно и эффективно управлять дробными числами, обеспечивая возможность выполнять арифметические операции, сравнения и другие действия. Основная задача класса — упрощение работы с дробями, предоставляя разработчикам гибкие инструменты для математических вычислений. Поэтому важно правильно использовать этот класс, чтобы избежать ошибок и получить точные результаты.

• два значения, где первое — это числитель, а второе — знаменатель (переменная a);
• дробное значение в виде строки (переменная b);
• вещественное значение (переменная c);
• другой Fraction, так как Fraction и является реализацией рационального дробного значения (переменная d).

Переменная Fraction отображает дробное представление рационального числа 0,5. При преобразовании значения ½ в тип float мы получаем его вещественное представление. Это демонстрирует, как различные типы данных могут влиять на форматирование и отображение чисел в программировании. Понимание этих различий важно для правильной работы с математическими операциями и их результатами в коде.

Изменим значения переменных и рассмотрим свойства рациональных чисел, используя в качестве примеров отрицательную дробь -¾, дробь ⅔ с бесконечным периодом и целое число 10. Анализ таких чисел позволяет лучше понять их характеристики и взаимосвязи. Начнём с отрицательной дроби -¾, которая указывает на значение меньше нуля. Далее, дробь ⅔ с бесконечным периодом демонстрирует, как рациональные числа могут принимать форму, где десятичное представление продолжается бесконечно. Наконец, целое число 10 служит отличным примером положительного рационального числа. Исследование этих значений помогает углубить понимание рациональных чисел и их свойств в математике.

Рассмотрим свойство ассоциативности сложения, используя формулу (a + b) + c = a + (b + c). Это позволяет нам подтвердить равенство значений. Также преобразуем дроби в формат с плавающей запятой (float) для упрощения вычислений.

При анализе данных можно заметить, что значения идентичны, однако при их представлении в вещественном формате возникает число с бесконечным периодом 6. Как упоминалось ранее, такие числа также классифицируются как рациональные.

Рассмотрим применение распределительного свойства умножения. Мы проведем аналогичную операцию, чтобы проиллюстрировать это свойство в действии. Распределительное свойство умножения позволяет нам умножать сумму чисел на число, что упрощает вычисления и делает их более понятными. Эта методика широко используется в математике для решения различных задач. Теперь давайте применим данное свойство на практике.

Полученные значения равны, однако наблюдается нарушение периодичности рационального числа при переводе его в вещественный вид: 3 в конце округляется до 4. Это связано с особенностями вычислений в языке Python. Если на бумаге разделить 5 на 6, получится 0,8333…, где 3 повторяется бесконечно.

В заключение рассмотрим деление рациональных чисел с применением переместительного свойства. Начнем с деления числа a на b. Затем поменяем местами операнды и проанализируем результат. Для этого умножаем a на дробь 1/b, используя класс Fraction, который отвечает за реализацию дробей. Таким образом, мы получаем новый результат.

Резюме: повторим изученное

В данной статье мы рассмотрели понятие рациональных чисел, их отличительные черты по сравнению с другими типами чисел, а также основные свойства. Теперь давайте кратко подытожим ключевые моменты для лучшего понимания темы.

• Рациональное число — это число, которое можно представить в виде дроби, где числитель — целое число, а знаменатель — натуральное.
• Рациональные числа — это все натуральные и целые числа, а также дроби: обыкновенные, конечные десятичные и бесконечные периодические.
• Бесконечные периодические дроби — это такие дроби, где есть повторяющаяся последовательность после запятой. Например, 1,16161616… Если дробь бесконечная, а такой последовательности нет, число называется иррациональным.
• У рациональных чисел есть математические свойства: переместительное, сочетательное, распределительное и так далее.
• С рациональными числами можно проводить любые математические операции, такие как сложение, вычитание, деление, умножение и другие.

Узнайте больше о кодировании и программировании в нашем телеграм-канале. Подписывайтесь, чтобы не пропустить интересные материалы и полезные советы!

Для оптимизации текста под SEO, важно использовать ключевые слова и фразы, которые соответствуют теме. Вот переработанный текст:

Исследуйте дополнительные материалы:

Ваши рекомендации по выбору литературы и ресурсов помогут углубить знания и расширить кругозор. Чтение полезных статей, публикаций и книг способствует развитию навыков и понимания текущих трендов. Не упустите возможность ознакомиться с актуальными исследованиями и новыми идеями, которые могут быть полезны в вашей деятельности. Обратите внимание на авторитетные источники, которые обеспечат вас качественной информацией и актуальными данными.

• Двоичная (бинарная) система счисления: что это и как ей пользоваться
• Тест: что вы знаете про Джона Маккарти — автора термина «ИИ» и языка Lisp?
• 30 мощных нейросетей для любых задач

Узнайте больше о кодировании и программировании в нашем телеграм-канале. Подписывайтесь, чтобы не пропустить увлекательные материалы и полезные советы!