Кратчайший путь на графе: Алгоритмы Дейкстры и А*

Содержание:

• Введение в теорию графов: основы и приложения
• Принципы работы алгоритма Дейкстры
• История создания алгоритма Дейкстры: от идеи до внедрения
• Алгоритм Дейкстры на Python: Пошаговая реализация
• Алгоритм A*: Обзор и Применение
• Эффективная реализация алгоритма A* на Python
• Сравнение алгоритмов Дейкстры и A*: Что выбрать?

Введение в теорию графов: основы и приложения

Теория графов — ключевая область математики и информатики, посвященная изучению графов, состоящих из вершин и рёбер. Графы играют важную роль в моделировании систем и взаимосвязей, которые можно встретить в реальной жизни. Они используются в различных сферах, таких как компьютерные науки, социальные сети, транспортные системы и многие другие. Понимание графов позволяет анализировать сложные структуры и оптимизировать процессы, делая теорию графов незаменимым инструментом в современных исследованиях и технологиях.

Алгоритм Дейкстры является эффективным методом для поиска кратчайших путей в графах. Он позволяет определить минимальное расстояние от одной вершины к другим, что делает его незаменимым в таких сферах, как навигация, транспортные системы и анализ сетей. Благодаря своей универсальности и быстродействию, алгоритм Дейкстры широко используется в приложениях, где требуется оптимизация маршрутов и минимизация затрат.

Графы бывают направленными и ненаправленными, в зависимости от характера связи между вершинами. Рёбра графов могут иметь веса, которые отражают силу или стоимость связи. К примеру, в графах социальных сетей вершинами выступают пользователи, а рёбрами являются дружеские связи. Эти связи можно оценивать по частоте обмена сообщениями, что позволяет анализировать взаимодействия в сети. Графы играют важную роль в различных областях, таких как анализ данных, компьютерные сети и социальные исследования, обеспечивая эффективные методы для представления и обработки информации о взаимосвязях.

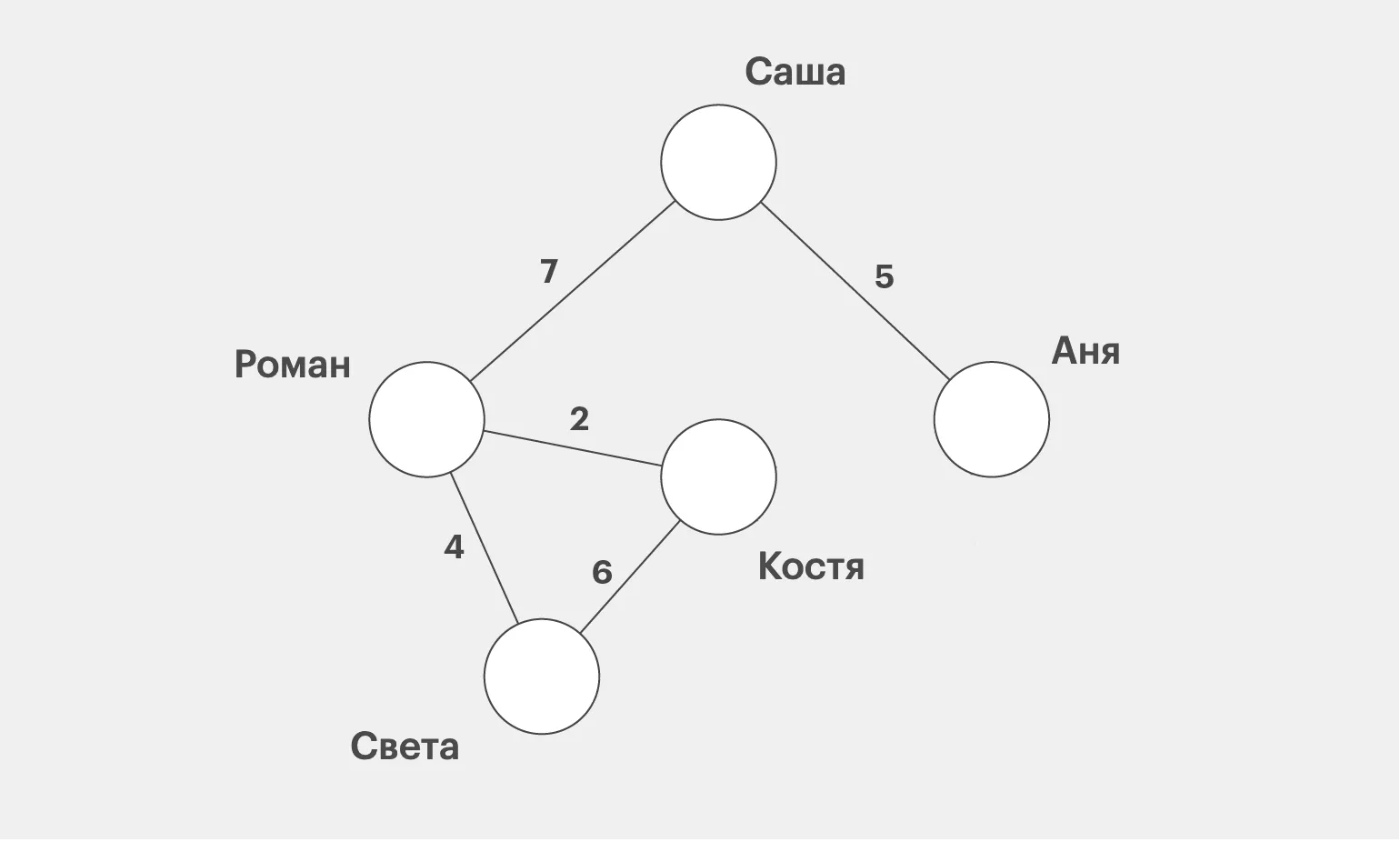
Применение графов выходит за рамки социальных сетей и охватывает множество различных областей. Графы активно используются в компьютерных науках для анализа сетевой структуры, в транспортной логистике для оптимизации маршрутов, а также в биоинформатике для моделирования взаимодействий между биологическими молекулами. В финансах графы помогают в выявлении связей между активами, а в телекоммуникациях — в управлении сетевыми узлами. Таким образом, графы играют ключевую роль в решении сложных задач в самых разных сферах, обеспечивая эффективное представление и обработку данных.

• моделирование веб-страниц и их взаимосвязей в интернете;
• проектирование дорожных сетей, где вершины представляют улицы, а рёбра — перекрёстки;
• изучение взаимодействий генов, белков и молекул в биоинформатике;
• оптимизация логистических маршрутов для доставки товаров;
• управление движением роботов в автоматизированных системах.

Принципы работы алгоритма Дейкстры

Алгоритм Дейкстры представляет собой эффективный метод для нахождения кратчайших путей в графах. Он позволяет быстро вычислять минимальные расстояния от одной вершины к другим, что делает его незаменимым в задачах маршрутизации и в поисковых системах. Применение алгоритма Дейкстры позволяет значительно оптимизировать процессы, связанные с определением наиболее коротких маршрутов, что особенно важно в таких областях, как транспорт, телекоммуникации и компьютерные сети. Использование данного алгоритма способствует повышению эффективности и скорости обработки данных, что актуально для современных технологий.

В современных условиях, когда планирование маршрутов стало важной частью повседневной жизни, существует множество способов найти кратчайший путь между городами, например, A, B, C, D, E и F. Чтобы определить оптимальный маршрут от города A до города C, можно воспользоваться алгоритмами, такими как алгоритм Дейкстры или алгоритм A*. Эти методы позволяют эффективно анализировать дорожную сеть и находить минимальное расстояние между двумя точками.

Для начала необходимо создать карту, на которой будут указаны расстояния между всеми городами. Затем следует применить один из упомянутых алгоритмов, который проведет анализ возможных маршрутов, выбирая наиболее короткий путь. Важно учитывать не только расстояние, но и возможные препятствия, такие как пробки или закрытые дороги, которые могут повлиять на время в пути.

Использование картографических сервисов и навигационных приложений также значительно упрощает задачу поиска кратчайшего пути. Эти технологии могут предоставить актуальную информацию о дорожной ситуации и предложить оптимальные маршруты в реальном времени. Таким образом, для быстрого нахождения кратчайшего пути от города A до города C необходимо использовать алгоритмы поиска и современные навигационные инструменты, что сделает путешествие более удобным и эффективным.

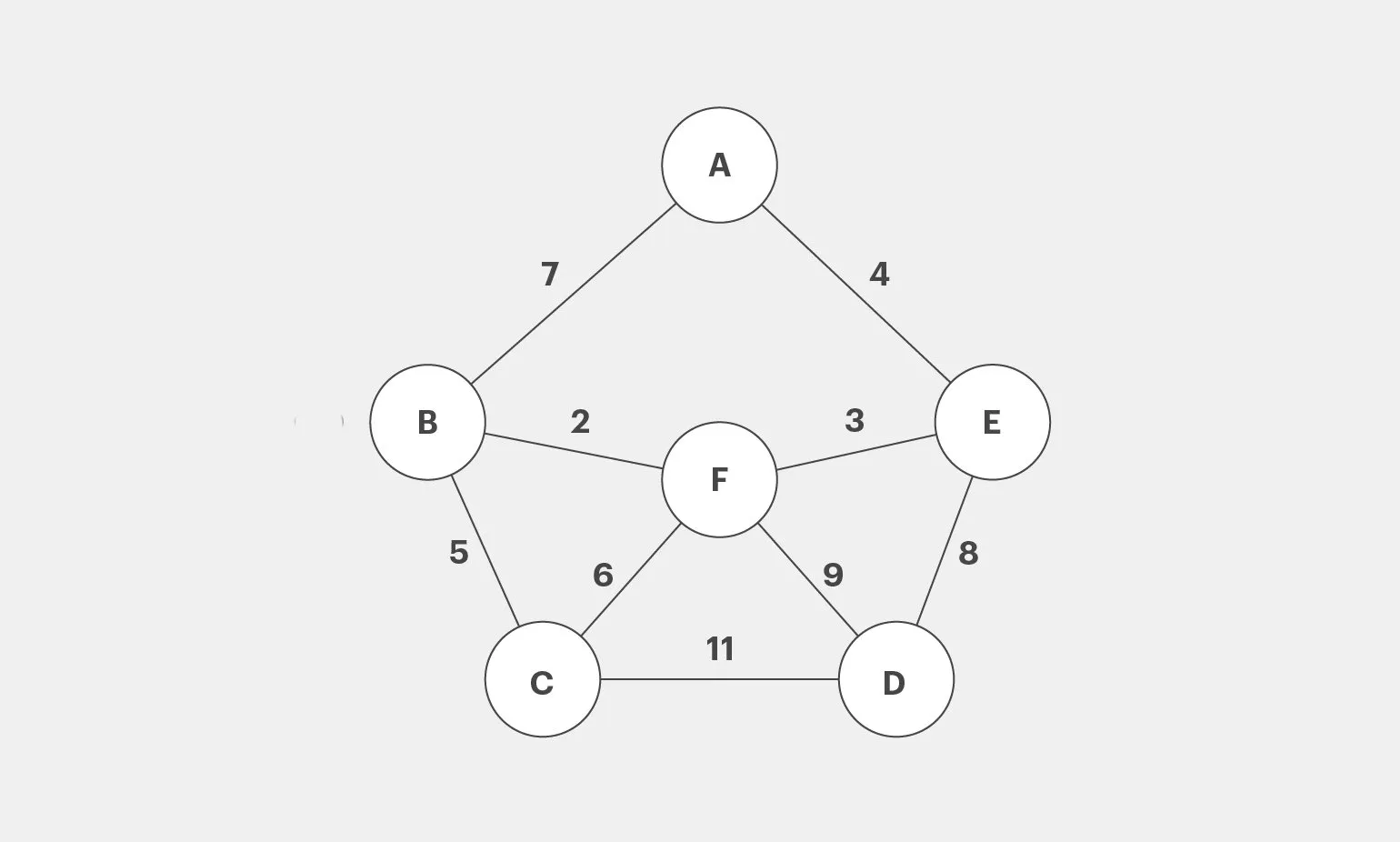
На первый взгляд, задача выбора кратчайшего маршрута между городами может показаться простой: необходимо сравнить все возможные маршруты, например, A → B → C. Однако, с увеличением числа городов (вершин), количество возможных маршрутов возрастает экспоненциально, что делает задачу значительно более сложной. Это явление связано с комбинаторным взрывом, когда при добавлении каждой новой вершины количество комбинаций увеличивается многократно. В результате, для эффективного поиска кратчайшего пути необходимо применять алгоритмы оптимизации и теории графов, такие как алгоритм Дейкстры или алгоритм A*, которые значительно сокращают время вычислений и позволяют находить оптимальные маршруты даже в сложных сетях.

При наличии более 26 городов даже самый мощный суперкомпьютер может потребовать миллиарды лет для перебора всех возможных маршрутов. В таких ситуациях на помощь приходит алгоритм Дейкстры, который эффективно решает задачи поиска кратчайшего пути. Этот алгоритм позволяет значительно сократить время расчета, оптимизируя процесс нахождения наилучшего маршрута между городами. Алгоритм Дейкстры является ключевым инструментом в области теории графов и широко используется в различных приложениях, включая навигационные системы и логистику.

Данный алгоритм не просто перебирает все возможные варианты, а применяет жадный подход. Он последовательно выбирает вершины с наименьшим расстоянием, продвигаясь к заданной цели. Такой метод существенно сокращает время вычислений и обеспечивает получение оптимальных результатов. Использование жадного алгоритма эффективно для задач поиска кратчайшего пути, что делает его популярным в различных областях, таких как графовые структуры и маршрутизация.

Вернемся к нашей задаче и начнем с определения минимальных расстояний от города A до всех других городов: B, C, D, E и F. Это позволит нам лучше понять связь между этими точками и оптимизировать маршруты для дальнейших расчетов.

На первом этапе зададим начальные значения расстояний от вершины A. Для самой вершины A расстояние будет равно 0, а для всех остальных вершин установим значение бесконечность, так как на данный момент у нас отсутствуют данные о расстояниях до них.

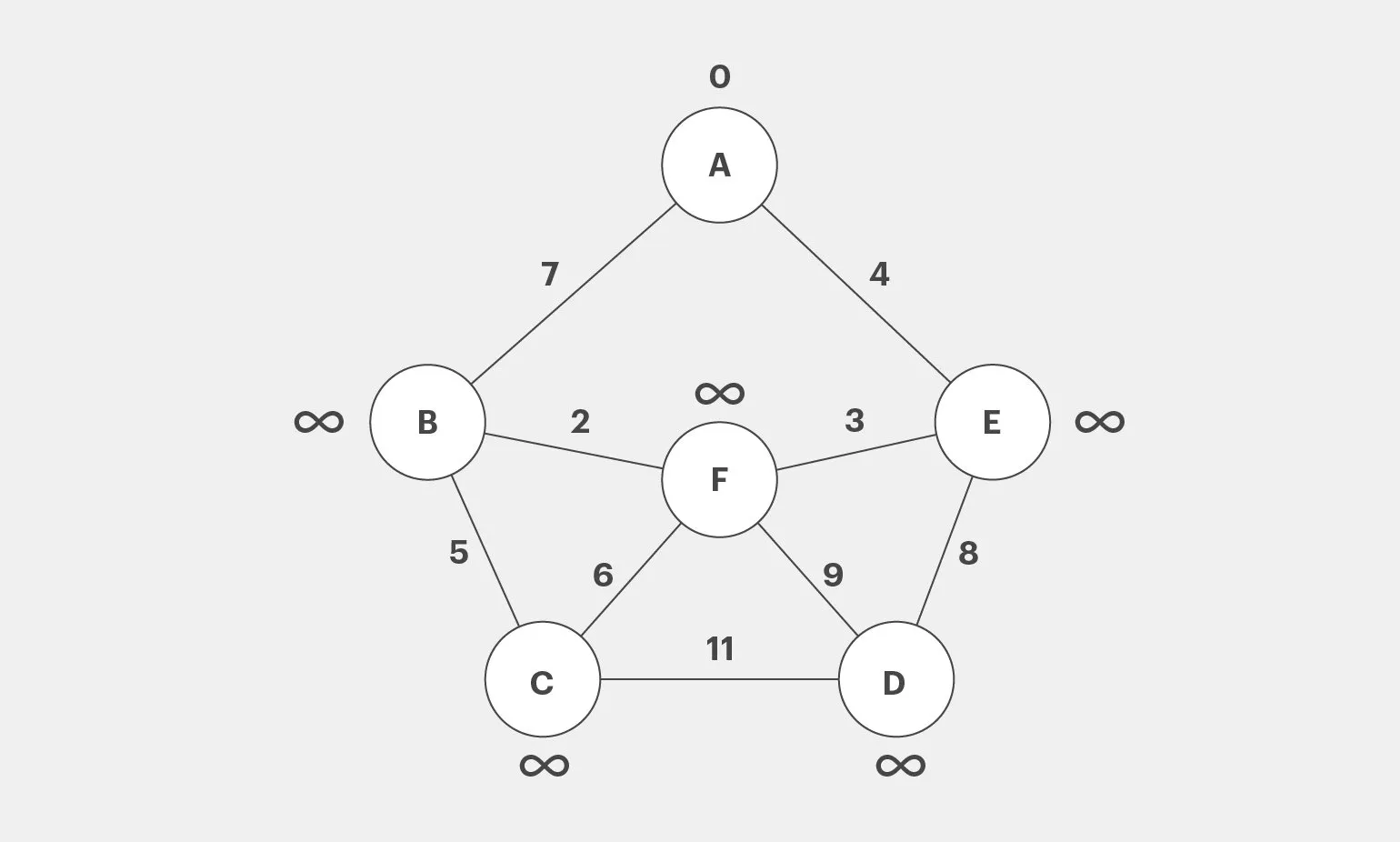
Рассмотрим соседние вершины A, которыми являются B и E, расстояния до которых составляют 7 и 4 соответственно. Поскольку эти значения меньше бесконечности, обновим их в нашей модели. Вершину A отметим как посещенную. Это позволит нам более точно оценить путь и продолжить анализ графа.

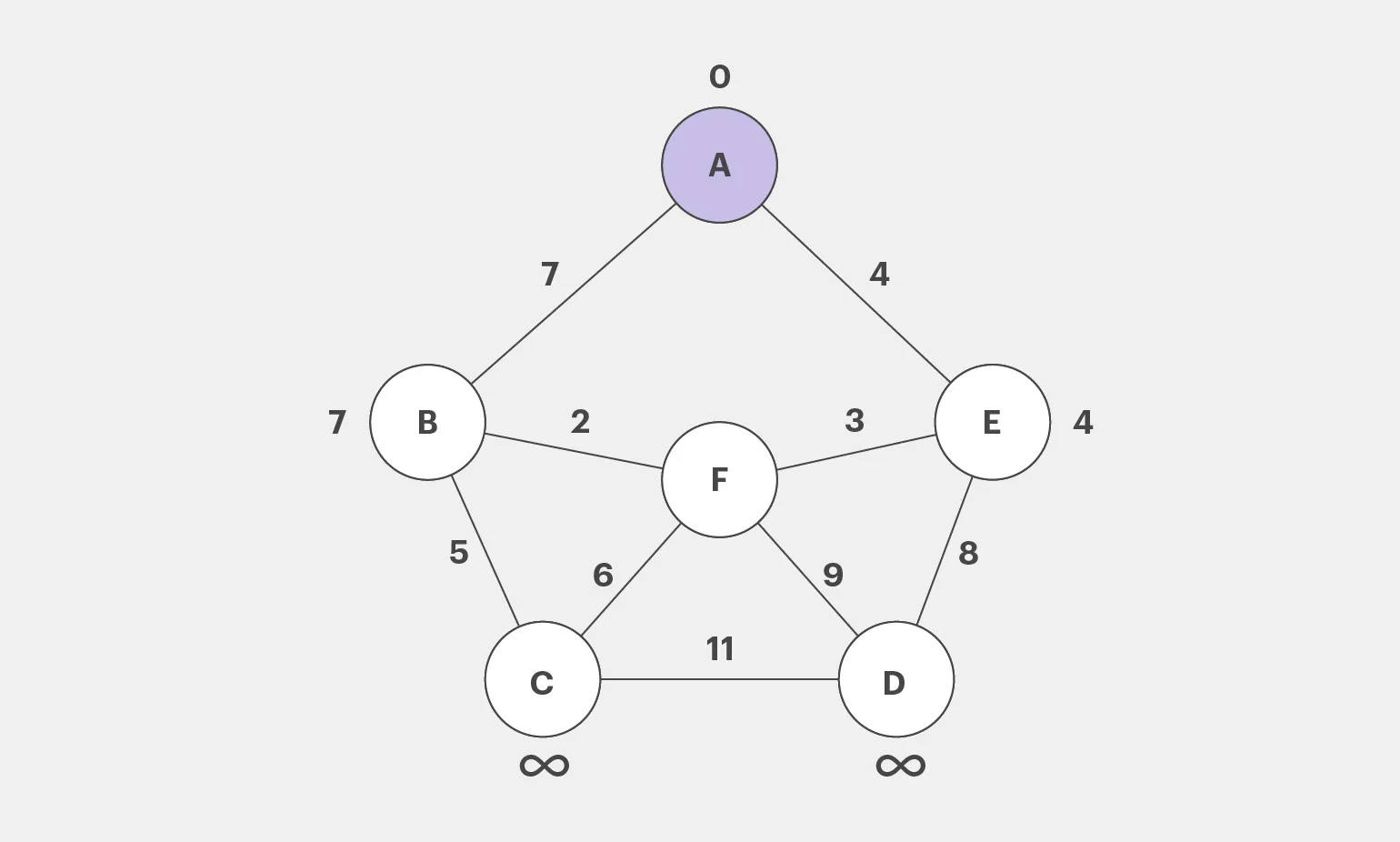
Теперь обратимся к вершине с минимальным расстоянием, то есть к E. Её соседями, которые ещё не были посещены, являются вершины F и D. Рассчитаем расстояния до этих вершин:

• Для F: 4 + 3 = 7
• Для D: 4 + 8 = 12

Поскольку новые значения оказались ниже предыдущих, необходимо произвести их обновление. Вершина E будет также отмечена как посещённая.

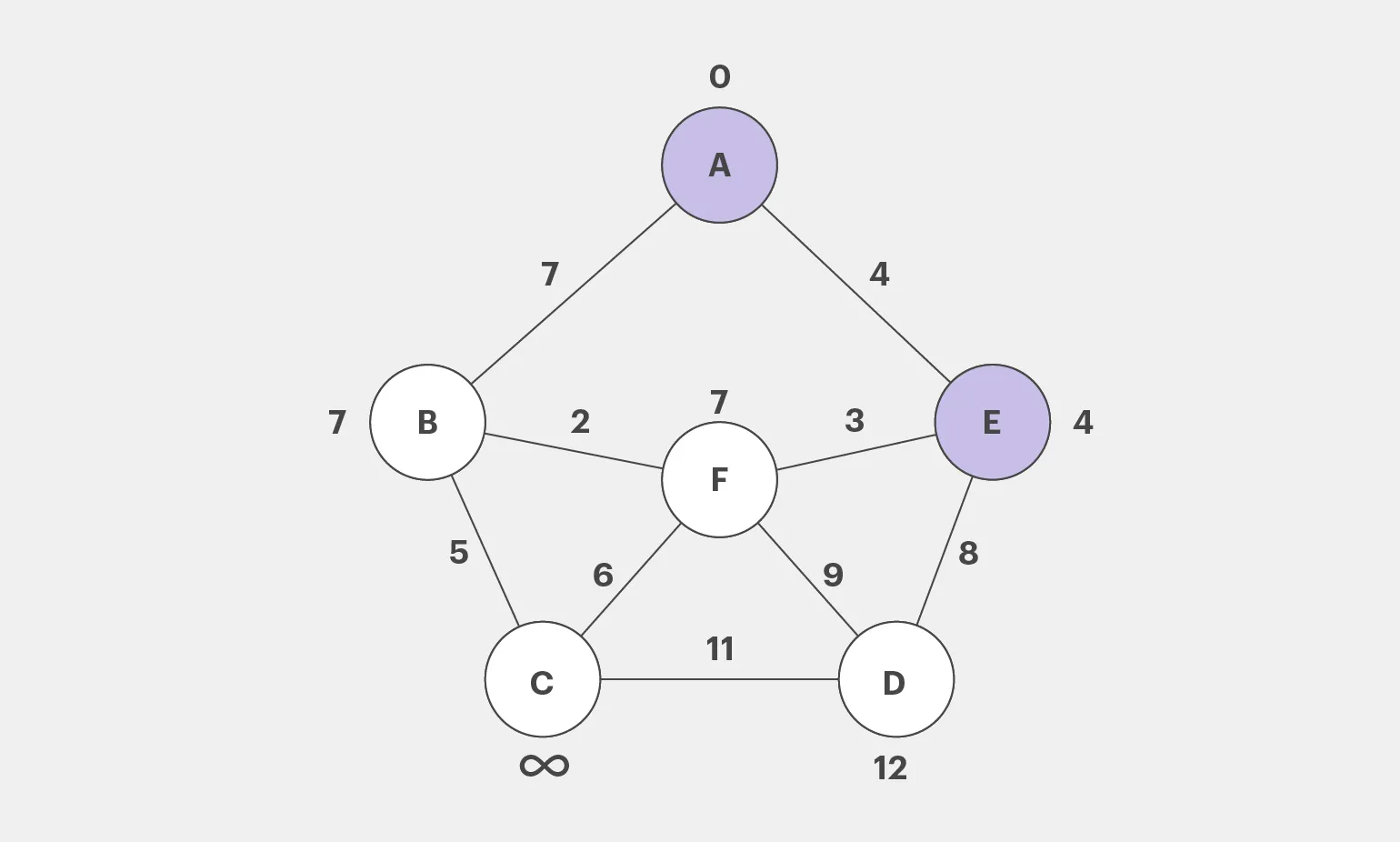
Алгоритм продолжает выбирать непосещенные вершины с минимальными значениями и выполнять расчеты, пока не будет определено кратчайшее расстояние для каждой вершины. Этот процесс обеспечивает эффективное нахождение оптимальных путей в графах, что является ключевым аспектом в задачах маршрутизации и сетевого анализа.

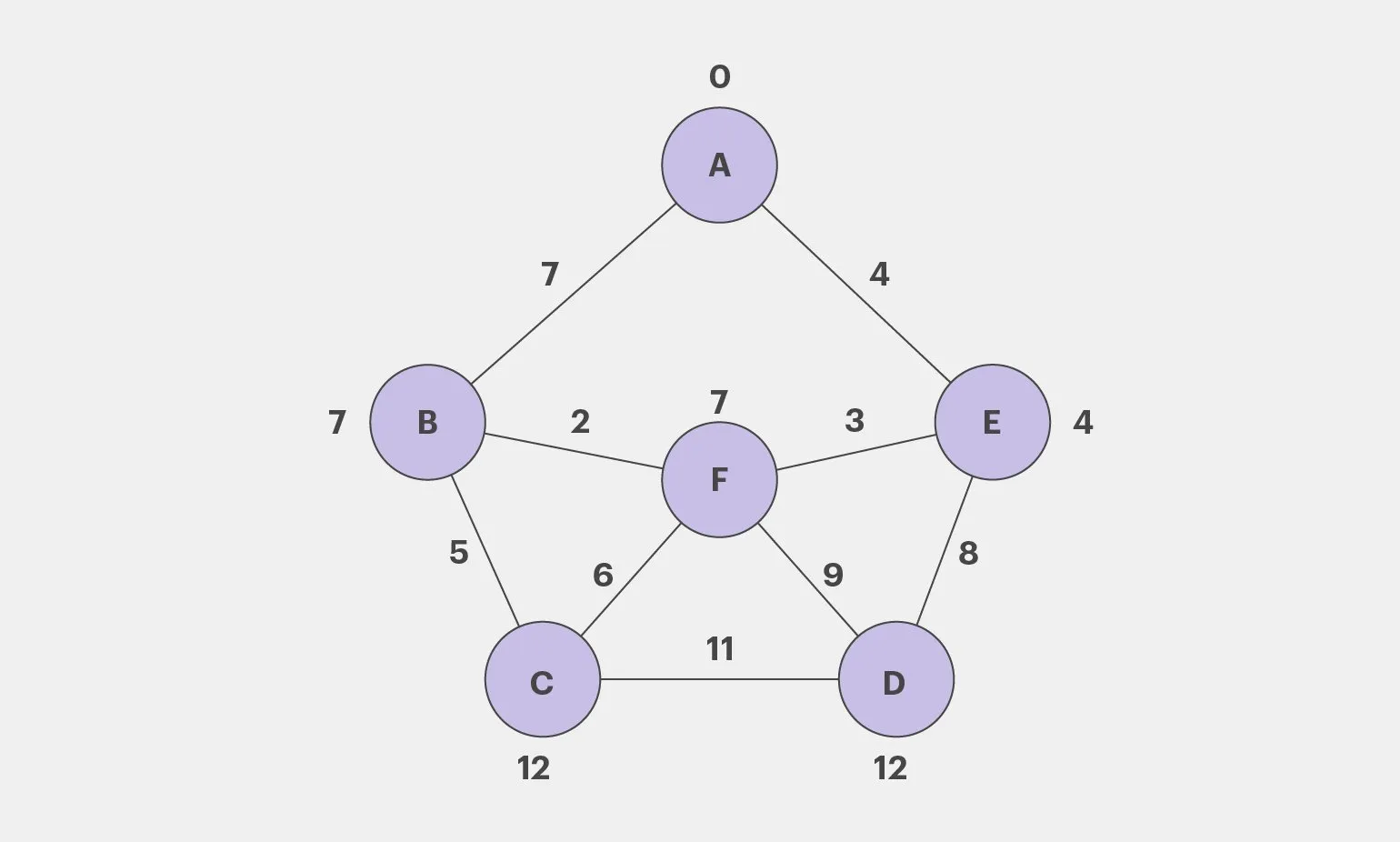
С помощью нашего метода можно определить кратчайшие маршруты от точки A до других городов. Например, мы можем найти оптимальные пути, учитывающие различные факторы, такие как расстояние, время в пути и условия на дорогах. Это позволит эффективно планировать поездки и минимизировать затраты на транспортировку. Оптимизация маршрутов не только улучшает логистику, но и повышает удобство передвижения для пользователей.

• От A до F: A — E — F
• От A до D: A — E — D
• От A до C: A — B — C

Алгоритм Дейкстры обладает определёнными ограничениями. Он может быть использован исключительно для взвешенных графов, в которых заранее известны веса рёбер. Важно отметить, что эти веса должны быть неотрицательными. Если граф содержит отрицательные веса рёбер, алгоритм Дейкстры не обеспечит корректные результаты. Поэтому для работы с графами, где могут присутствовать отрицательные веса, рекомендуется применять альтернативные алгоритмы, такие как алгоритм Беллмана-Форда.

История создания алгоритма Дейкстры: от идеи до внедрения

Алгоритм Дейкстры, разработанный голландским ученым Эдсгером Дейкстрой в 1956 году, стал основой для многих современных приложений в области компьютерных наук и навигации. Дейкстра стремился продемонстрировать возможности нового компьютера ARMAC и искал задачу, доступную для понимания даже тем, кто не имел опыта работы с вычислительной техникой. Этот алгоритм эффективно решает задачи поиска кратчайших путей в графах, что делает его незаменимым инструментом в различных областях, от геоинформационных систем до разработки сетевых протоколов. Алгоритм Дейкстры продолжает оставаться актуальным и востребованным среди специалистов, работающих с большими объемами данных и сложными сетевыми структурами.

Эдсгер Дейкстра разработал алгоритм поиска кратчайшего пути, который стал основой для программного обеспечения, используемого для построения маршрутов на транспортной карте Нидерландов. Этот алгоритм значительно упростил процесс планирования поездок, что стало важным шагом вперед в логистике и транспортной сфере. Благодаря его разработке стало возможным эффективно находить оптимальные маршруты, что положительно сказалось на качестве транспортных услуг и улучшило управление передвижением.

Алгоритм Дейкстры был разработан в непринужденной обстановке. В одном из своих интервью Дейкстра поделился воспоминанием о том, как во время кофе с невестой на террасе кафе в Амстердаме он за двадцать минут создал алгоритм для нахождения кратчайшего пути. Этот алгоритм был опубликован три года спустя, в 1959 году. Алгоритм Дейкстры стал основой для многих приложений в области оптимизации маршрутов и является важным инструментом в графовой теории.

Одной из причин элегантности и эффективности алгоритма является его разработка в уме, без использования бумаги и карандаша. Дейкстра отметил, что одно из преимуществ такого подхода заключается в стремлении минимизировать сложности. Этот метод проектирования способствует более ясному мышлению и позволяет сосредоточиться на ключевых аспектах задачи, что в свою очередь приводит к созданию более оптимальных решений.

Алгоритм Дейкстры представляет собой значимое достижение в сфере математики и информатики. Он стал ключевым фактором, способствующим популярности Эдсгера Дейкстры как ученого. Сам Дейкстра отмечал, что этот алгоритм стал, к его удивлению, одним из краеугольных камней его славы. Алгоритм используется для нахождения кратчайшего пути в графах и находит применение в различных областях, включая сети, транспортные системы и навигационные приложения. Его эффективность и простота сделали его одним из самых известных и широко используемых алгоритмов в компьютерных науках.

Для более полного понимания алгоритма и его практического применения, полезно изучить материалы на сайте GeeksforGeeks и Википедии. Эти ресурсы содержат подробные объяснения алгоритма Дейкстры, его реализацию с использованием приоритетных очередей, а также примеры использования в различных задачах. Ознакомление с этими материалами поможет лучше grasp основные принципы работы алгоритма и его эффективность в нахождении кратчайших путей в графах.

Алгоритм Дейкстры продолжает находить применение в различных областях, таких как навигационные системы и анализ сетей, что подчеркивает его универсальность и значимость в современных технологиях. Эта эффективная методика поиска кратчайшего пути позволяет оптимизировать маршруты и улучшать качество обслуживания в таких сферах, как транспорт, телекоммуникации и геоинформационные системы. Использование алгоритма Дейкстры способствует повышению точности и скорости обработки данных, что делает его незаменимым инструментом для разработчиков и исследователей.

Алгоритм Дейкстры на Python: Пошаговая реализация

Теперь, когда мы изучили теоретические основы, перейдем к практической части и разработаем код, реализующий алгоритм Дейкстры на языке Python. В данном примере мы будем определять кратчайшие расстояния от вершины A до всех остальных вершин в графе. Алгоритм Дейкстры является эффективным методом для решения задач поиска кратчайших путей в графах с неотрицательными весами ребер. Создадим функцию, которая будет принимать граф в виде словаря и вершину-источник, а затем возвращать кратчайшие расстояния до всех вершин.

Для эффективной работы алгоритма необходимо использовать модуль heapq, который входит в стандартную библиотеку Python. Этот модуль предоставляет возможности для работы с кучами — уникальной структурой данных, в которой значение родительского узла всегда меньше или равно значениям его дочерних узлов. Такое свойство кучи позволяет быстро извлекать минимальный элемент, что делает её полезной для различных алгоритмов, включая сортировку и реализацию приоритетных очередей. Использование heapq значительно оптимизирует операции вставки и удаления, что особенно важно при обработке больших объемов данных.

Создадим функцию dijkstra, которая принимает два аргумента: graph, представляющий наш граф, и start, обозначающий начальную вершину. Эта функция будет реализовывать алгоритм Дейкстры для поиска кратчайшего пути от начальной вершины до всех остальных вершин графа. Алгоритм Дейкстры эффективен для работы с графами, где все рёбра имеют неотрицательные веса, и позволяет найти минимальные расстояния до каждой вершины. В реализации функции мы будем использовать приоритетную очередь для оптимизации поиска.

Внутри функции мы инициализируем словарь distances, который будет хранить расстояния от начальной вершины до всех остальных вершин графа. Кроме того, создадим кучу priority_queue для удобного извлечения вершин с наименьшими текущими расстояниями. Это позволит оптимизировать процесс поиска кратчайших путей и улучшить общую эффективность алгоритма.

Алгоритм будет последовательно обновлять расстояния до соседних вершин, пока не найдет кратчайшие пути ко всем вершинам в графе. Результаты работы алгоритма будут представлены в виде словаря, в котором ключами являются вершины графа, а значениями — минимальные расстояния от начальной точки A до каждой из этих вершин. Этот подход позволяет эффективно находить кратчайшие пути, что является важным аспектом в задачах, связанных с графами и оптимизацией маршрутов.

Теперь мы произведем расчёт кратчайших расстояний для нашего графа. Для этого граф будет представлен в формате словаря, где ключи соответствуют вершинам, а значения — это словари, содержащие соседние вершины и веса рёбер. Такой подход позволяет эффективно обрабатывать данные и находить оптимальные пути между вершинами, что является ключевым элементом в теории графов и алгоритмах поиска.

После создания графа необходимо вызвать функцию Дейкстры, передав ей в качестве начальной вершины вершину A. Результат выполнения функции будет выведен в консоль. Такой подход позволяет эффективно находить кратчайший путь от начальной вершины к другим вершинам графа.

Мы успешно завершили реализацию алгоритма Дейкстры на Python. Этот алгоритм позволяет находить кратчайшие пути в графах, что делает его незаменимым инструментом в задачах оптимизации маршрутов. Теперь вы можете использовать наш код для решения различных задач, связанных с анализом графов и поиском оптимальных маршрутов. Применение алгоритма Дейкстры открывает новые возможности для разработки приложений в области навигации, логистики и сетевого анализа.

Если вас интересуют дополнительные сведения и примеры применения данного алгоритма, советую посетить ресурсы, такие как GeeksforGeeks и Python.org. Эти сайты предлагают обширную информацию и практические примеры, которые помогут лучше понять алгоритм и его использование в различных сценариях.

Алгоритм A*: Обзор и Применение

Алгоритм A*, произносимый как «А звезда», является эффективным инструментом для решения задач поиска кратчайшего пути. Разработанный в 1968 году, он нашел широкое применение в таких областях, как робототехника, навигационные системы и разработка видеоигр. A* представляет собой усовершенствованную версию алгоритма Дейкстры, добавляющую дополнительные функции, которые значительно увеличивают скорость и эффективность поиска пути. Благодаря своей способности учитывать как стоимость перемещения, так и оценку оставшегося расстояния до цели, алгоритм A* обеспечивает оптимальные решения в сложных условиях.

Алгоритм A* является эффективным методом поиска оптимального пути от начальной точки до конечной, аналогично алгоритму Дейкстры. Однако A* выделяется тем, что он сочетает два ключевых компонента: фактическое расстояние от начальной точки и эвристическую оценку расстояния до целевой точки. Эвристика в данном случае представляет собой приближенную оценку, которая позволяет значительно ускорить процесс поиска, делая его более интеллектуальным. Благодаря этой комбинации, алгоритм A* обеспечивает более быстрое нахождение оптимального пути в различных приложениях, таких как навигационные системы и игры.

Для определения кратчайшего пути между городами A и B можно использовать эвристическую функцию, такую как евклидово расстояние. Это расстояние представляет собой прямую линию от текущей точки до целевой, что позволяет более эффективно оценивать возможные маршруты. Применение евклидова расстояния в алгоритмах поиска пути, таких как A*, значительно ускоряет процесс нахождения оптимального маршрута, так как такая оценка помогает избежать ненужных обходов и направляет поиск в сторону наиболее перспективных вариантов. Таким образом, использование эвристических функций является ключевым элементом в задачах оптимизации маршрутов.

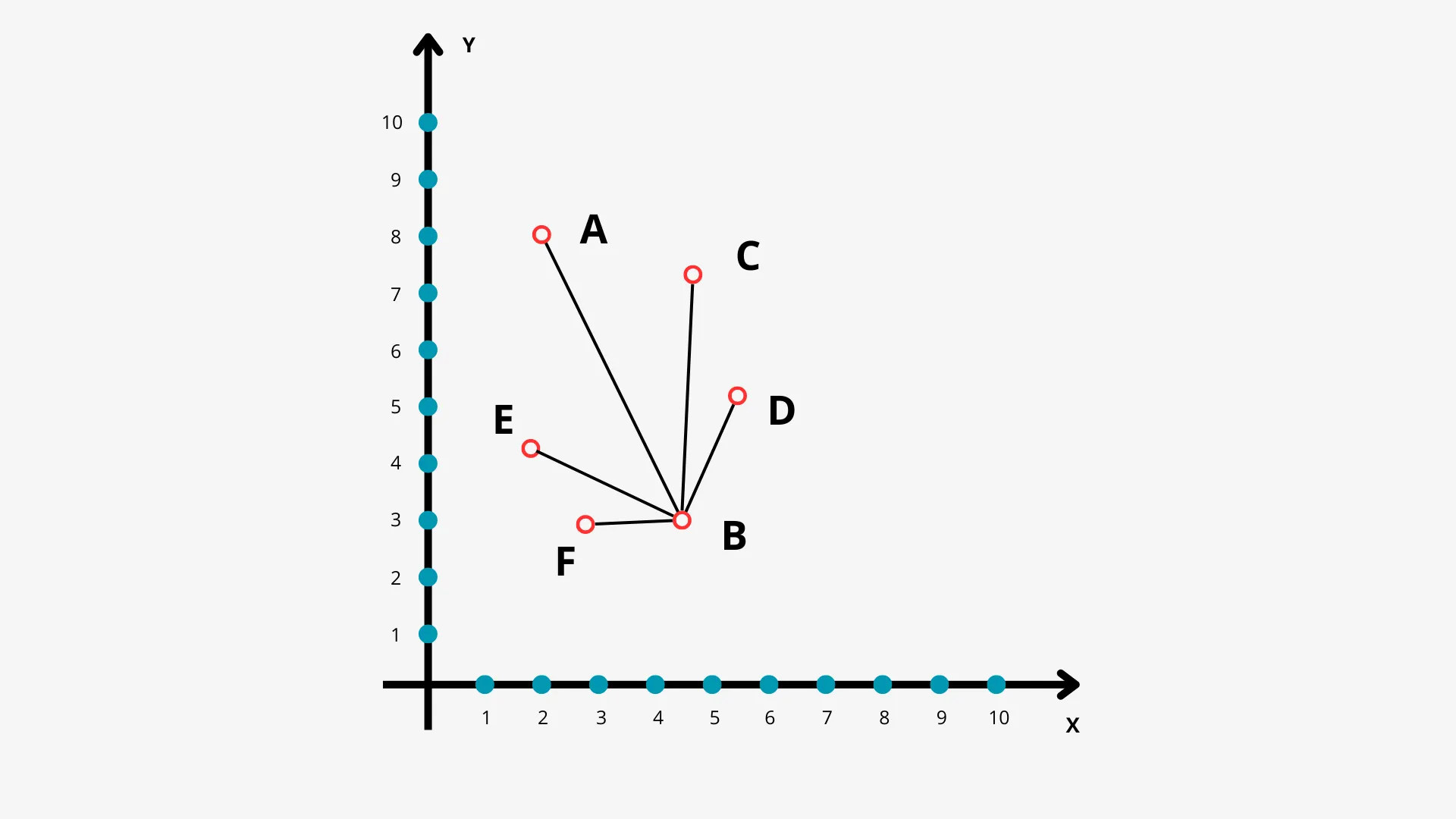
На представленном графике отображены эвристические расстояния от промежуточных точек до конечной цели, при этом не учитываются действующие дорожные маршруты. Это позволяет лучше понять общую структуру маршрута и оценить возможные пути достижения цели. Визуализация помогает выявить оптимальные направления движения и потенциальные уклонения от привычных маршрутов, что может быть полезно для планирования поездок или анализа транспортной инфраструктуры.

Манхэттенское расстояние является одной из известных эвристических функций, используемых в различных областях, включая компьютерные науки и оптимизацию маршрутов. Название этой функции происходит от характерной системы улиц Нью-Йорка, где улицы пересекаются под прямыми углами. В таких условиях для перемещения между двумя точками необходимо следовать параллельно осям координат. Это делает манхэттенское расстояние особенно подходящим для оценки маршрутов в городских условиях, где движение часто ограничено прямыми линиями. Использование этой эвристики позволяет эффективно решать задачи, связанные с поиском кратчайшего пути и оптимизацией логистики в урбанистических средах.

Для вычисления манхэттенского расстояния между двумя точками с координатами (x1, y1) и (x2, y2) используется простая формула. Манхэттенское расстояние, также известное как городское расстояние, определяется как сумма абсолютных разностей их координат. Формула выглядит следующим образом:

D = |x1 — x2| + |y1 — y2|.

Эта формула позволяет быстро оценить расстояние между двумя точками на плоскости, перемещаясь только по вертикали и горизонтали, что делает её особенно полезной в различных областях, таких как логистика, робототехника и игры. Понимание манхэттенского расстояния помогает оптимизировать маршруты и минимизировать затраты при перемещении объектов в городских условиях.

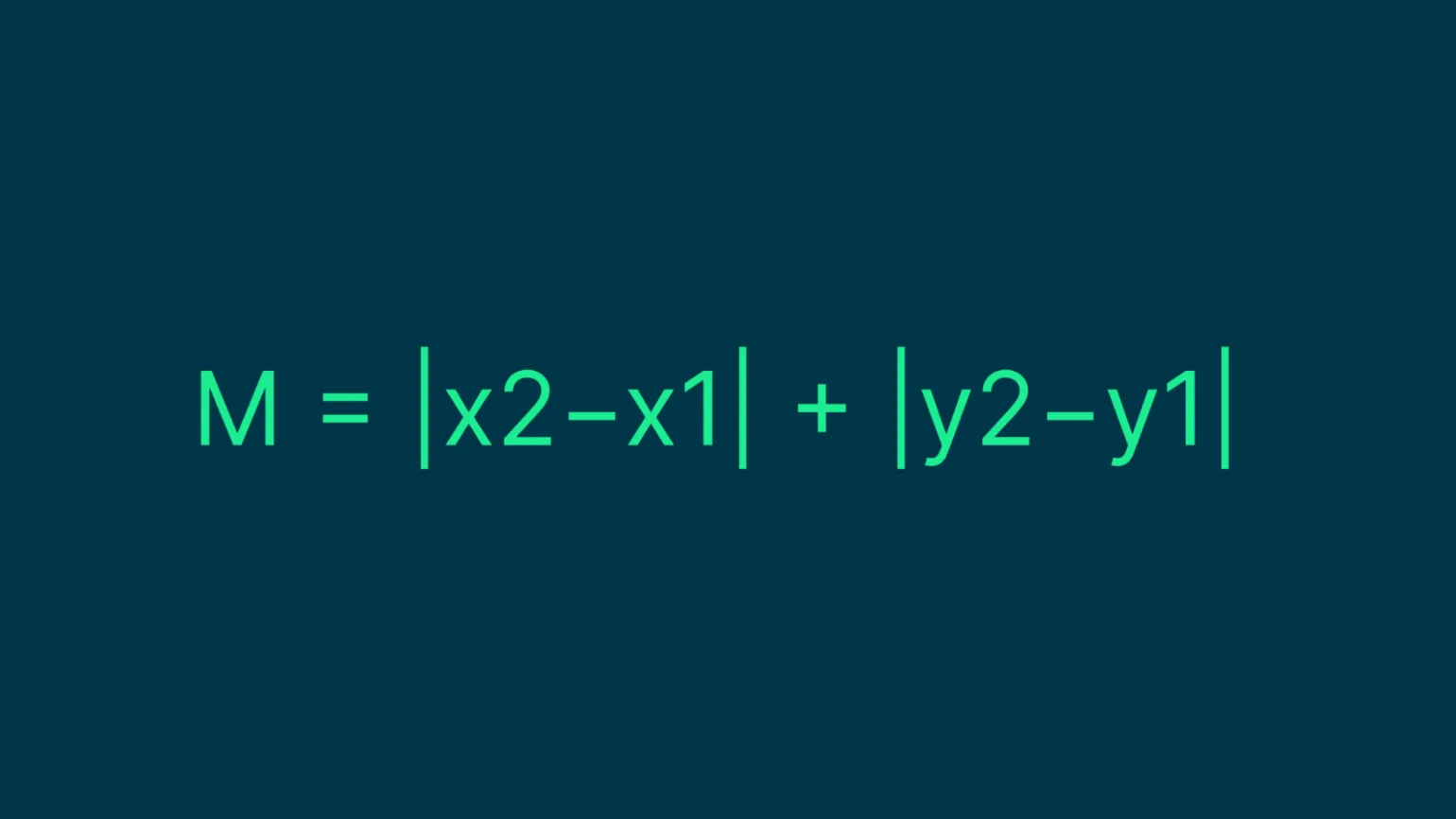
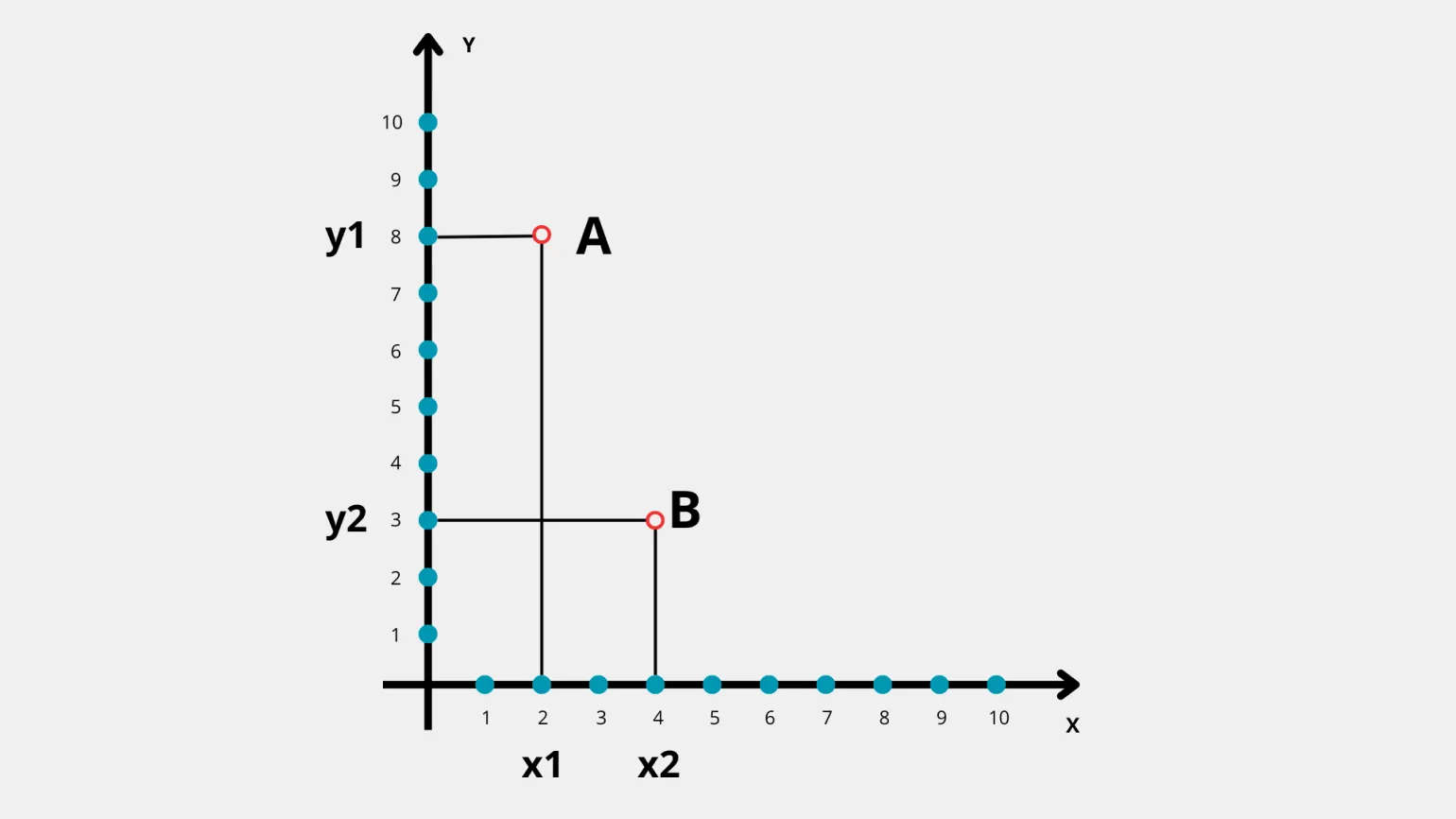
Рассмотрим пример вычисления манхэттенского расстояния. Пусть точка A находится в координатах (2, 8), а точка B — в координатах (4, 3). Подставив эти значения в формулу расчета манхэттенского расстояния, мы получаем: M = |4−2| + |3−8| = 2 + 5 = 7. Таким образом, манхэттенское расстояние между точками A и B составляет 7. Этот метод полезен для анализа расстояний в городских условиях, где передвижение происходит по прямым улицам.

Алгоритм A* основывается на вычислении двух основных значений для каждой вершины графа. Первое значение – это стоимость пути от начальной вершины до текущей, а второе – это оценка оставшейся стоимости пути от текущей вершины до целевой. Алгоритм сочетает в себе свойства поиска по ширине и жадного поиска, что позволяет эффективно находить кратчайший путь. При этом A* использует эвристическую функцию, которая помогает оценить расстояние до цели, что значительно ускоряет процесс поиска. Применение A* находит свое место в различных областях, таких как планирование маршрутов, игры и робототехника, благодаря своей способности находить оптимальные решения при минимальных затратах времени.

• g(n) — это длина пути от начальной вершины до текущей вершины n.
• h(n) — эвристическая оценка расстояния от текущей вершины n до цели.

Алгоритм A* на каждом этапе выбирает вершину с минимальной суммой g(n) + h(n), тщательно исследуя соседние вершины. Этот процесс продолжается до достижения конечной цели. Современные исследования подтверждают, что алгоритм A* продолжает оставаться одним из самых эффективных решений для задач поиска пути в реальном времени. Его применение охватывает различные области, включая робототехнику, игровую разработку и маршрутизацию, что делает его незаменимым инструментом для оптимизации поиска и повышения эффективности.

Эффективная реализация алгоритма A* на Python

Рассмотрим реализацию алгоритма A* на Python с использованием манхэттенского расстояния в качестве эвристики. Алгоритм A* является эффективным методом для поиска кратчайшего пути в графах, что делает его особенно полезным для двумерных сеток. В данной статье мы обсудим ключевые аспекты работы алгоритма и приведем пример его реализации на языке Python. Использование манхэттенского расстояния позволяет эффективно оценивать расстояние до цели, что существенно ускоряет процесс поиска. Алгоритм A* сочетает в себе преимущества алгоритмов Дейкстры и жадных методов, что делает его оптимальным выбором для задач по поиску путей.

Алгоритм A* является эффективным методом поиска пути, который сочетает в себе фактическое расстояние от начальной точки до текущей и эвристическую оценку расстояния до цели. В данном контексте для вычисления манхэттенского расстояния между двумя точками в сетке применяется функция manhattan_distance. Этот подход позволяет алгоритму A* находить оптимальные маршруты в различных задачах, таких как навигация в играх или планирование маршрутов в робототехнике. Учитывая как реальные, так и предполагаемые расстояния, алгоритм A* обеспечивает более быстрое и точное решение по сравнению с другими методами поиска.

Основные этапы реализации алгоритма A* включают в себя следующие элементы:

Первым шагом является инициализация начальной и целевой точки, где определяются координаты и значения, необходимые для работы алгоритма. Далее необходимо создать два списка: открытый, который будет содержать узлы, подлежащие оценке, и закрытый, в который будут помещаться проверенные узлы.

Затем начинается основной цикл алгоритма, в котором происходит выбор узла с наименьшей стоимостью из открытого списка. Этот узел оценивается на наличие соседей, которые могут стать частью пути. Для каждого соседа вычисляются значения f, g и h, где f – это общая стоимость пути, g – стоимость от начальной точки до текущего узла, а h – оценка стоимости пути от текущего узла до целевой точки.

Если сосед еще не добавлен в открытый список, он добавляется в него. Если он уже находится в этом списке, то сравниваются значения g, и при необходимости обновляется путь. После обработки всех соседей текущий узел перемещается в закрытый список.

Процесс продолжается до тех пор, пока открытый список не станет пустым или пока не будет найден целевой узел. В случае нахождения целевой точки алгоритм возвращает найденный путь, который оптимален по заданным критериям.

Таким образом, алгоритм A* эффективно находит кратчайший путь в графах, используя комбинацию эвристики и оценок стоимости.

Определение сетки 5 × 5, где препятствия представлены единицами, является первым шагом в создании системы для нахождения кратчайшего пути. Далее необходимо реализовать функцию восстановления пути, которая позволит отслеживать оптимальный маршрут от точки А до точки B. После этого можно запустить алгоритм A*, который выполняет поиск наилучшего пути с учетом заданных препятствий, и отобразить полученные результаты. Этот процесс обеспечит эффективное решение задачи навигации в ограниченном пространстве.

После выполнения данного алгоритма вы получите оптимальный маршрут от точки А до точки B. Это и будет конечным результатом работы кода, который обеспечивает нахождение кратчайшего пути.

Этот пример иллюстрирует эффективное применение алгоритма A* для поиска оптимального маршрута в сетке, используя манхэттенское расстояние в качестве эвристической функции. Алгоритм A* является мощным инструментом для решения задач навигации и маршрутизации, позволяя находить наилучшие пути в различных приложениях, от мобильных карт до робототехники. Использование манхэттенского расстояния помогает значительно ускорить процесс поиска, обеспечивая более быстрые и точные результаты.

Для получения более подробной информации и примеров кода рекомендуется обратиться к официальной документации Python по ссылке https://docs.python.org/3/. Также полезно изучить ресурсы, посвященные алгоритмам, например, информацию о алгоритме A* на сайте https://www.geeksforgeeks.org/a-star-search-algorithm/. Эти ресурсы помогут вам углубить знания и лучше понять применение различных алгоритмов и библиотек в Python.

Сравнение алгоритмов Дейкстры и A*: Что выбрать?

При выборе алгоритма для поиска кратчайшего пути между алгоритмами Дейкстры и A* следует учитывать особенности конкретной задачи и доступные данные. Каждый из этих алгоритмов обладает уникальными преимуществами и недостатками. Оптимальность их применения зависит от контекста, в котором они используются, а также от требований к производительности и точности поиска. Алгоритм Дейкстры хорошо подходит для задач, где необходимо находить кратчайший путь в графах с равными весами, в то время как A* более эффективно решает задачи с эвристическим подходом, что позволяет быстрее находить оптимальные решения в больших и сложных графах.

Ключевые различия между этими двумя подходами заслуживают более детального анализа. Обе стратегии имеют свои уникальные особенности, которые могут значительно повлиять на результаты. Важно учитывать не только их преимущества, но и недостатки, чтобы сделать осознанный выбор. Рассмотрим, как каждый из подходов влияет на эффективность и результаты, а также какие факторы следует принимать во внимание при принятии решения.

• Алгоритм Дейкстры предназначен для нахождения кратчайшего пути от одной стартовой вершины ко всем остальным вершинам графа. В отличие от него, алгоритм A* ориентирован на нахождение кратчайшего пути к конкретной цели, используя эвристическую функцию для оценки расстояния.
• Одно из главных отличий заключается в том, что алгоритм Дейкстры рассматривает все вершины как равные и выбирает ту, которая находится наименьшем расстоянии от начальной. Алгоритм A*, в свою очередь, использует эвристическую оценку, что делает его более быстрым и эффективным, особенно в больших и сложных графах.
• Алгоритм Дейкстры может быть менее эффективным на больших графах, так как он прорабатывает все возможные вершины, что увеличивает время выполнения. Алгоритм A* значительно ускоряет процесс поиска, благодаря своей способности игнорировать менее перспективные пути.

Алгоритм Дейкстры является отличным выбором для определения кратчайших путей от одной вершины ко всем остальным в графах, особенно когда отсутствует эвристическая информация. Его эффективность проявляется в ситуациях, когда требуется надежное и точное решение. В то же время, если доступна эвристическая информация, которая может ускорить процесс поиска, алгоритм A* значительно улучшает производительность и позволяет быстрее находить оптимальные пути. Выбор между алгоритмами зависит от конкретных условий задачи и доступных данных.

При выборе между алгоритмами Дейкстры и A* важно учитывать специфику задачи, размеры графа и наличие эвристической информации. Алгоритм Дейкстры идеально подходит для поиска кратчайшего пути в графах с равными весами ребер, тогда как A* более эффективен в ситуациях, где доступна эвристика, что позволяет ускорить процесс поиска решения. Для более глубокого изучения и применения этих алгоритмов стоит обратиться к ресурсам, таким как GeeksforGeeks и Wikipedia, которые предлагают подробные объяснения, примеры и практические советы.