Статистика для дата-сайентистов: 7 ключевых понятий

Содержание:

• 1. Основные концепции описательной статистики
• 2. Понимание распределения данных
• 3. Семплирование: Искусство выбора
• 4. Понимание смещения в моделировании
• Что такое дисперсия и её значение в статистике
• Понимание дисперсии: как она влияет на анализ данных
• 6. Дилемма смещения и дисперсии в машинном обучении
• 7. Корреляция: Понимание и Применение

1. Основные концепции описательной статистики

Описательная статистика является важным инструментом в анализе данных, так как она предоставляет детальное описание и обобщение характеристик наборов данных. В отличие от предсказательной статистики, основная цель описательной статистики заключается в том, чтобы представить данные в ясной и доступной форме. Это позволяет исследователям и аналитикам лучше понимать структуру и особенности данных, выявлять закономерности и тренды. Описательная статистика включает такие меры, как средние значения, медиана, мода, дисперсия и стандартное отклонение, которые помогают охарактеризовать распределение данных и его характеристики. Использование описательной статистики является первым шагом в анализе, позволяющим подготовить данные для дальнейшего исследования и интерпретации.

Основные показатели, применяемые в описательной статистике, включают в себя ключевые меры центральной тенденции. Эти меры позволяют обобщить данные и выявить их основные характеристики. К ним относятся среднее значение, медиана и мода, которые помогают анализировать распределение и поведение исследуемых данных. Правильное использование этих показателей позволяет более точно интерпретировать результаты и делать обоснованные выводы на основе статистической информации.

• Среднее: рассчитывается как среднее арифметическое, представляющее собой сумму всех значений, делённую на их количество. Это позволяет получить общее представление о данных.
• Медиана: для нахождения медианы необходимо отсортировать данные в порядке возрастания и определить среднее значение. Это значение делит набор данных на две равные части.
• Мода: определяется как значение, которое наиболее часто встречается в наборе данных. Моду легко запомнить: она представляет собой ‘самое популярное’ значение.

Рекомендуем ознакомиться с информативным видео о среднем, медиане и моде на платформе Академия Хана. Этот образовательный ресурс предоставляет понятные и доступные объяснения на русском языке, что делает изучение статистики более интересным и эффективным. Академия Хана поможет вам глубже понять эти важные статистические концепции и применить их в практике.

Помимо трех основных показателей, важно учитывать и другие статистические метрики, включая меры рассеяния. Одним из ключевых показателей является дисперсия, которая помогает глубже проанализировать, насколько сильно варьируются данные в пределах набора. Понимание дисперсии позволяет исследователям и аналитикам лучше интерпретировать данные, выявлять отклонения и делать обоснованные выводы. Анализ дисперсии также может быть полезен для оценки стабильности и надежности данных в различных исследованиях и проектах.

2. Понимание распределения данных

Распределение данных является важным аспектом анализа больших данных, позволяя выявить взаимосвязи между различными величинами. Аналогично тому, как по внешнему виду человека можно определить его возраст, пол и даже профессию, распределение данных помогает оценить структуру и особенности информационных массивов. Понимание распределения данных предоставляет аналитикам инструменты для более глубокого анализа и интерпретации результатов, что в свою очередь способствует принятию обоснованных решений в различных областях.

Термин «распределение» берёт своё начало в теории вероятностей, где каждое событие анализируется с точки зрения вероятности его возникновения. Даже если события происходят с разной частотой, они подчиняются определённому распределению, которое упорядочивает эти вероятности. Распределение позволяет исследовать закономерности случайных явлений и предсказывать вероятные исходы на основе имеющихся данных. Понимание распределений является ключевым элементом в статистике и вероятностных моделях, что делает его важным инструментом для анализа данных и принятия обоснованных решений.

В контексте Data Science распределение представляет собой закон взаимосвязи между величинами. Оно помогает выявить процессы, лежащие в основе данных, и оценить их полноту и качество. Понимание распределений критически важно для анализа данных и построения моделей. Если вы хотите углубить свои знания о математических основах в Data Science, рекомендуем ознакомиться с нашей статьей о математике для начинающих, где вы найдете полезную информацию и примеры.

Нормальное распределение, также именуемое гауссовым распределением, является одним из наиболее известных типов статистических распределений. Оно описывает ситуации, при которых итоговый результат представляет собой сумму множества независимых случайных величин, каждая из которых оказывает незначительное влияние на общий итог. Нормальное распределение играет ключевую роль в статистике и вероятностных расчетах, так как многие природные и социальные явления подчиняются его законам. Понимание нормального распределения важно для анализа данных и применения статистических методов, поскольку оно позволяет делать выводы о больших выборках на основе ограниченного объема информации.

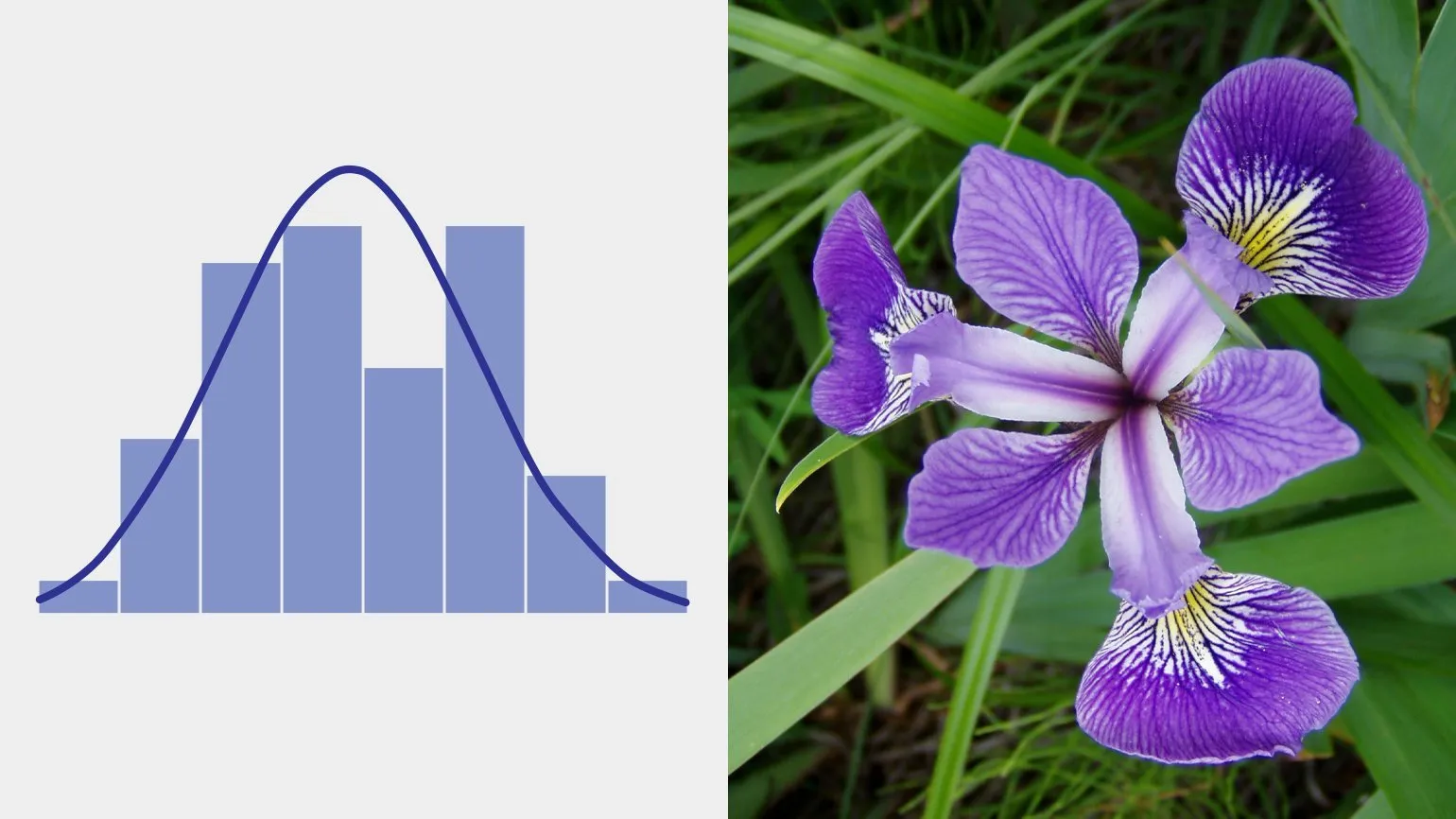
Нормальное распределение широко распространено в различных областях, от величины ошибок измерений в физике до биологических параметров, таких как длина когтей и зубов. Это распределение является одним из самых распространённых в природе, что подтверждает его значимость и универсальность. Нормальное распределение играет ключевую роль в статистике и научных исследованиях, так как многие природные явления подчиняются этому закономерному распределению. Понимание нормального распределения важно для анализа данных, что делает его незаменимым инструментом в научной и практической деятельности.

Распределение Пуассона является одним из наиболее распространённых статистических распределений, используемых для моделирования количества событий, происходящих в заданный интервал времени. Это распределение особенно актуально в случаях, когда события происходят независимо друг от друга и с постоянной интенсивностью. Например, распределение Пуассона часто применяется в таких областях, как теория вероятностей, статистика и различные прикладные науки, включая экономику и биологию. Оно позволяет эффективно анализировать редкие события, что делает его незаменимым инструментом для исследователей и специалистов.

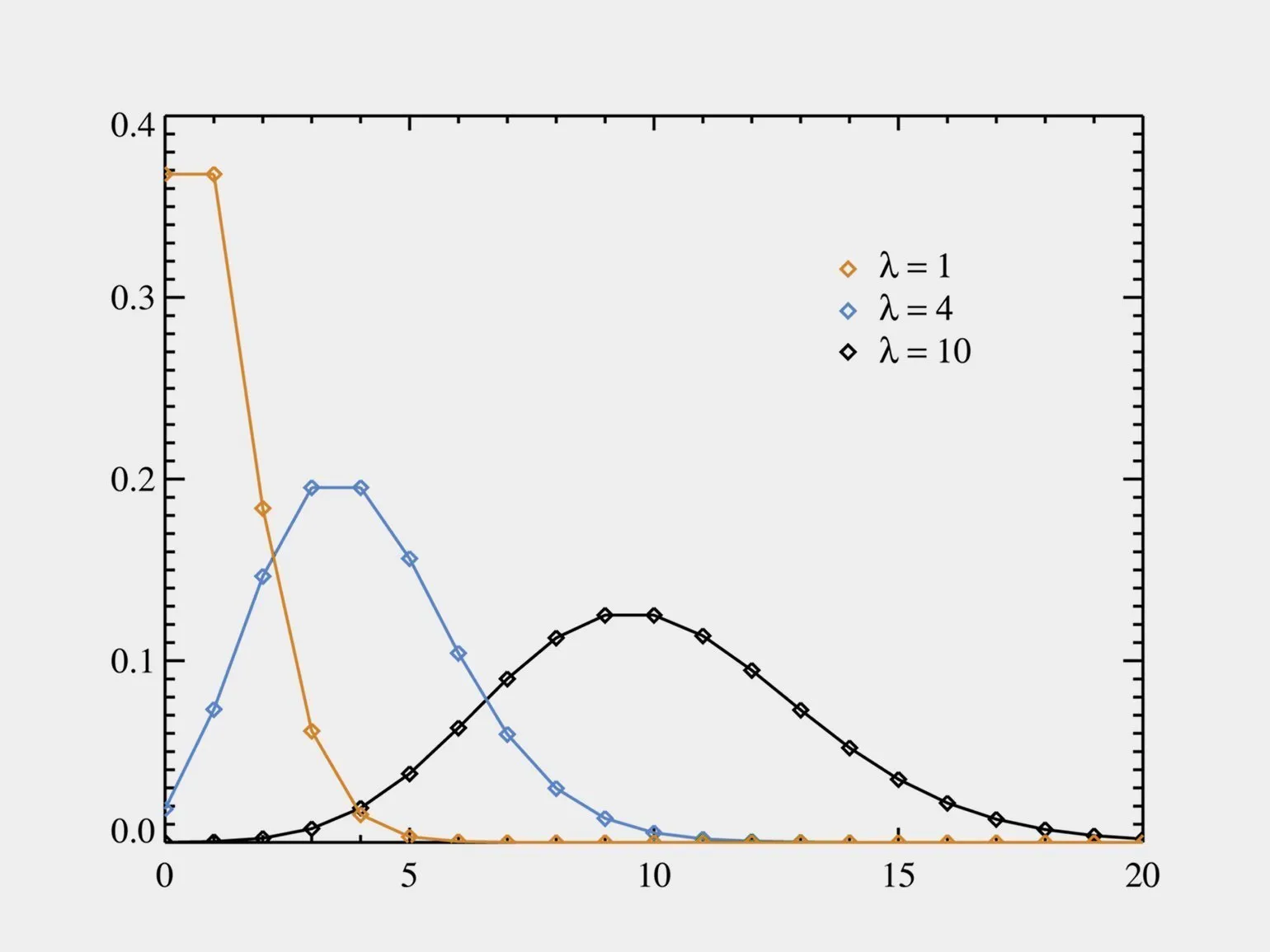
Распределение Пуассона широко используется в различных областях, включая подсчет числа посетителей в торговых центрах, анализ спортивных результатов и изучение роста колоний бактерий. Эта статистическая модель помогает исследовать редкие события и предсказывать вероятности их появления в заданный период времени. Благодаря своей универсальности, распределение Пуассона находит применение в таких сферах, как маркетинг, медицина и экология, позволяя специалистам эффективно обрабатывать и анализировать данные.

Существуют также менее распространенные распределения, такие как распределения Вигнера, Вейбулла и Коши. Эти распределения могут быть актуальны в специализированных областях, включая квантовую физику. Тем не менее, для дата-сайентистов важно иметь представление о ключевых распределениях, их графиках и параметрах. Знание этих аспектов существенно улучшает анализ данных и способствует более точной интерпретации результатов. Понимание основных распределений помогает в выборе правильных методов статистического анализа и моделирования, что является необходимым навыком в области науки о данных.

3. Семплирование: Искусство выбора

В современном мире, где данные играют важную роль в принятии решений, понимание семплирования становится крайне актуальным. Например, для определения средней ширины морды домашних котов в нашей стране невозможно измерить всех животных из-за ограничений во времени и ресурсах. В таких случаях необходимо использовать выборку — измерить морды определенного числа кошек и на основе этих данных сделать обоснованные выводы. Правильно проведенное семплирование позволяет получить точные и надежные результаты, которые могут быть использованы для анализа и принятия решений в различных областях.

Такой подход вызывает множество вопросов, требующих внимательного анализа.

• Какое количество и какие именно коты должны быть выбраны для замера?
• Почему следует выбрать именно этих животных, а не других?
• Какие гарантии существуют, что полученное среднее значение действительно отражает ширину морды всех котов России?

Семплирование — это важный набор статистических методов, позволяющий эффективно исследовать характеристики генеральной совокупности, например, всех котов в стране. Правильно организованное семплирование помогает сформировать выборку, которая максимально точно отражает разнообразие и особенности данной совокупности. Это критически важно для получения достоверных данных и выводов, что, в свою очередь, способствует более глубокому пониманию популяции котов и их поведения.

При проведении исследований о кошках необходимо учитывать, что простое измерение случайно выбранных особей не дает объективных результатов. Для получения достоверных данных важно использовать репрезентативную выборку, которая отражает общую популяцию. Такой подход позволяет делать обоснованные выводы и получать точные аналитические данные о различных характеристиках кошек. Релевантная выборка является ключом к успешному исследованию и обеспечению надежности результатов.

Статистика и кошки имеют интересную взаимосвязь. С выходом книги Владимира Савельева о статистике, многие начали связывать эти две темы. Книга предлагает уникальный взгляд на статистику через призму кошек, что делает ее особенно привлекательной для всех интересующихся данной областью. Рекомендуем ознакомиться с работой Савельева, чтобы глубже понять, как статистические данные могут быть связаны с повседневной жизнью, в том числе с нашими пушистыми друзьями.

Методы семплирования в Data Science являются ключевыми инструментами для создания, подготовки и оценки датасетов. Они помогают гарантировать, что данные структурированы и адекватно отражают реальность. Правильное семплирование позволяет избежать искажений и обеспечивает высокое качество анализа, что в свою очередь способствует более точным выводам и прогнозам. Эффективные техники семплирования помогают исследователям и аналитикам получать репрезентативные выборки, что критически важно для анализа больших объемов данных и принятия обоснованных решений.

4. Понимание смещения в моделировании

Смещение в модели машинного обучения является критически важным аспектом, способным значительно влиять на точность предсказаний. Оно возникает, когда алгоритм неправильно оценивает определенные параметры, что может привести к неверным выводам. Например, если туристическая модель предлагает всем жителям Краснодара поездки исключительно в Париж, игнорируя их индивидуальные предпочтения и финансовые возможности, это свидетельствует о смещении. В данном случае модель переоценивает параметр «Город проживания», что в итоге может привести к недовольству пользователей и снижению эффективности сервиса. Правильная настройка и оценка параметров модели необходимы для достижения более точных и персонализированных результатов.

Смещение в данных может быть вызвано различными факторами. К основным причинам относятся ошибки в сборе данных, некорректная обработка информации, влияние внешних факторов и изменения в методах измерения. Также стоит учитывать человеческий фактор, который может привести к искажению данных. Понимание причин смещения в данных крайне важно для анализа и интерпретации результатов, поскольку это позволяет избежать неверных выводов и улучшить качество принимаемых решений.

• Неправильный сбор данных: в выборку попадают только определенные группы, например, краснодарцы, которые любят Париж.
• Ошибки в формировании тренировочного набора.
• Недостаточная точность измерения ошибок.

Некорректный сбор данных может вызвать систематические ошибки в отборе информации. Например, в прошлом веке существовало мнение, что в космосе преобладают голубые галактики. Это мнение возникло из-за особенностей чувствительности фотопленки к голубой части спектра, что искажало действительность. Правильный сбор и анализ данных являются ключевыми для получения точных научных выводов и понимания космических объектов.

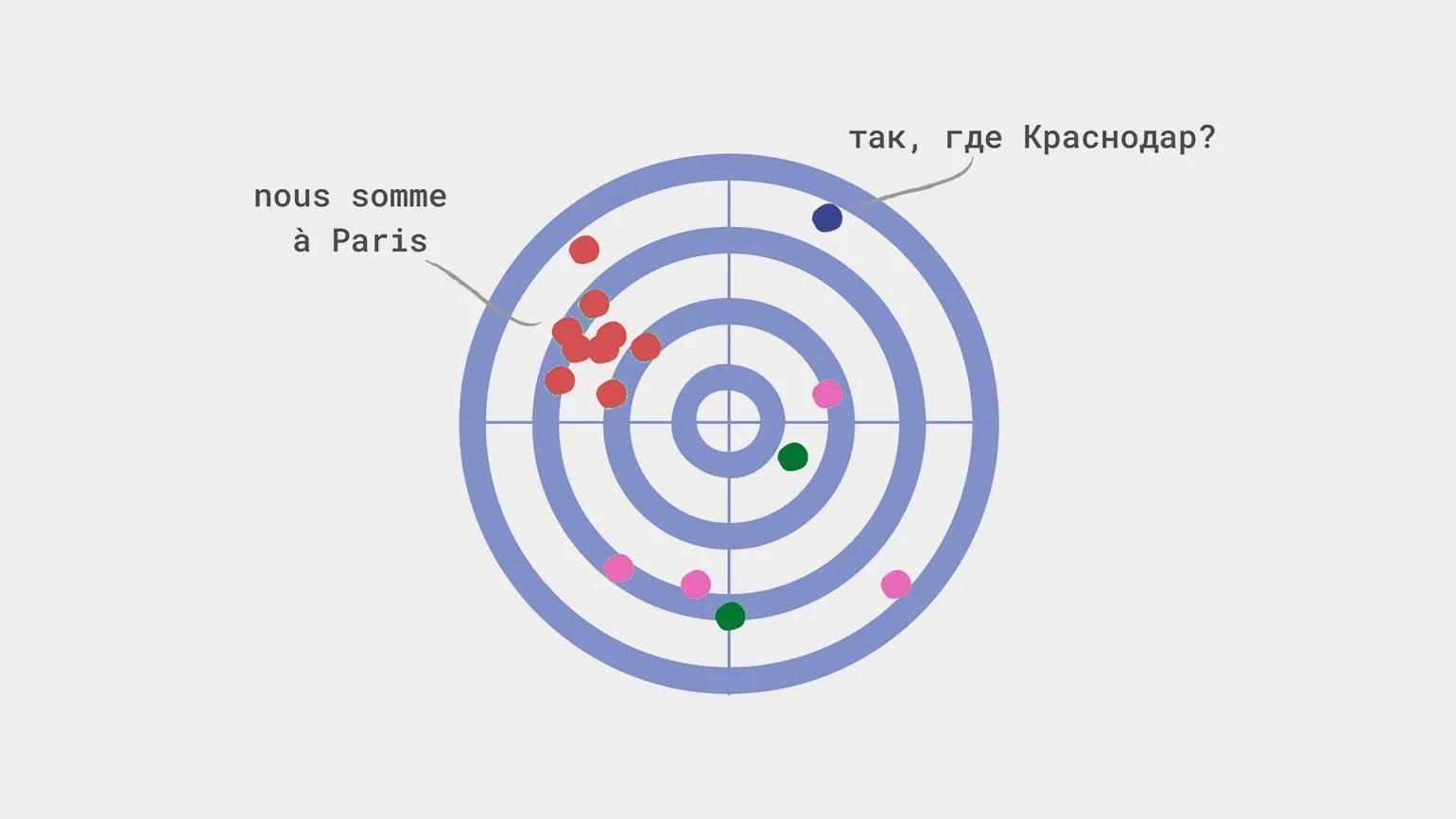
Одна из распространенных ошибок, называемая «ошибкой меткого стрелка», возникает, когда выборка данных формируется исключительно на основе схожих результатов. Это можно сравнить с ситуацией, когда стрелок рисует мишень вокруг тех мест, куда попал, вместо того чтобы оценить истинное положение дел. Такой подход приводит к искажению анализа и может привести к неверным выводам. Важно учитывать разнообразие данных и избегать предвзятости в выборке, чтобы получить более точные и надежные результаты.

Причины смещения данных столь разнообразны, что известный писатель Марк Твен подметил: «Существует три вида лжи: ложь, наглая ложь и статистика». К числу основных факторов, способствующих смещению, можно отнести выборочные выборки, предвзятость в интерпретации данных и искажения при сборе информации. Эти аспекты могут существенно повлиять на выводы и принятие решений, основанных на статистических данных. Понимание причин смещения критически важно для повышения точности анализа и обеспечения надежности результатов.

• Эффект низкой/высокой базы: если в финансовом отчете указать самый низкий уровень прибыли, любой другой показатель будет выглядеть как успех.
• Сокращение временного периода: чтобы доказать неэффективность рекламной кампании, достаточно выбрать период, когда деньги уже потрачены, а результатов нет.
• Исключение участников из выборки: если вы проводите исследование по снижению веса, можно исключить тех, кто прекратил методику, чтобы улучшить результаты.
• Классический случай: «Опрос показал, что 100% населения пользуются интернетом».

Ошибки смещения трудно обнаружить с помощью статистических методов, поэтому критически важно предотвращать их возникновение на этапе подготовки к сбору данных.

Если данные уже собраны и структурированы, важно задать себе несколько ключевых вопросов. Во-первых, нужно выяснить, не искажены ли ваши данные. В большинстве случаев они действительно могут быть искажены. Второй вопрос — это направление и причина искажения. Третий вопрос — возможно ли с этим смириться. Анализ этих аспектов поможет вам лучше понять качество данных и их влияние на ваши выводы.

Для более глубокого понимания методов борьбы со смещением и значимости правильной выборки данных важно изучить исследования на авторитетных платформах, таких как Towards Data Science и KDnuggets. Эти ресурсы предоставляют ценные материалы и актуальную информацию о том, как избежать смещения в данных и повысить качество аналитики. Обращение к данным источникам поможет углубить ваши знания и навыки в области анализа данных и машинного обучения, что крайне важно для успешного выполнения проектов в этой сфере.

Что такое дисперсия и её значение в статистике

Дисперсия — важное понятие в статистике и машинном обучении, которое показывает степень разброса значений относительно их математического ожидания. Она позволяет оценить, насколько результаты модели или финансовые доходы отклоняются от ожидаемого значения. Понимание дисперсии критически важно для анализа и оптимизации аналитических моделей, так как помогает оценить их точность и надежность. Уменьшение дисперсии может свидетельствовать о повышении стабильности предсказаний, что особенно актуально в контексте принятия бизнес-решений и разработки эффективных алгоритмов.

Дисперсия, как мера разброса, играет ключевую роль в анализе вариаций данных. Она позволяет оценить, насколько значения в наборе данных отклоняются от среднего. В качестве базового значения обычно используется математическое ожидание, которое можно теоретически определить для различных статистических распределений. Чаще всего простое среднее арифметическое служит в качестве этого ориентира. Понимание дисперсии и ее расчет имеет важное значение для статистического анализа, поскольку помогает выявить степень изменчивости данных и принимать обоснованные решения на основе полученных результатов.

Математическое ожидание броска стандартного игрального кубика можно рассчитать следующим образом: (1 + 2 + 3 + 4 + 5 + 6) / 6 = 21/6 = 3,5. Это значение представляет собой средний результат, который можно ожидать при большом количестве бросков кубика. Таким образом, математическое ожидание является важным понятием в теории вероятностей и помогает прогнозировать результаты случайных событий.

Представьте тир, где стрелок стремится попасть в центр мишени. Попадание в центр приносит максимальные 10 баллов, а удаление от центра снижает баллы вплоть до 1 балла на краю мишени. Каждый выстрел можно рассматривать как случайное значение в диапазоне от 1 до 10, что наглядно демонстрирует принцип дисперсии. Данная ситуация иллюстрирует, как случайные факторы влияют на результаты, а также важность точности и контроля в достижении максимального результата. Понимание дисперсии может быть полезным в различных областях, от статистики до принятия решений в условиях неопределенности.

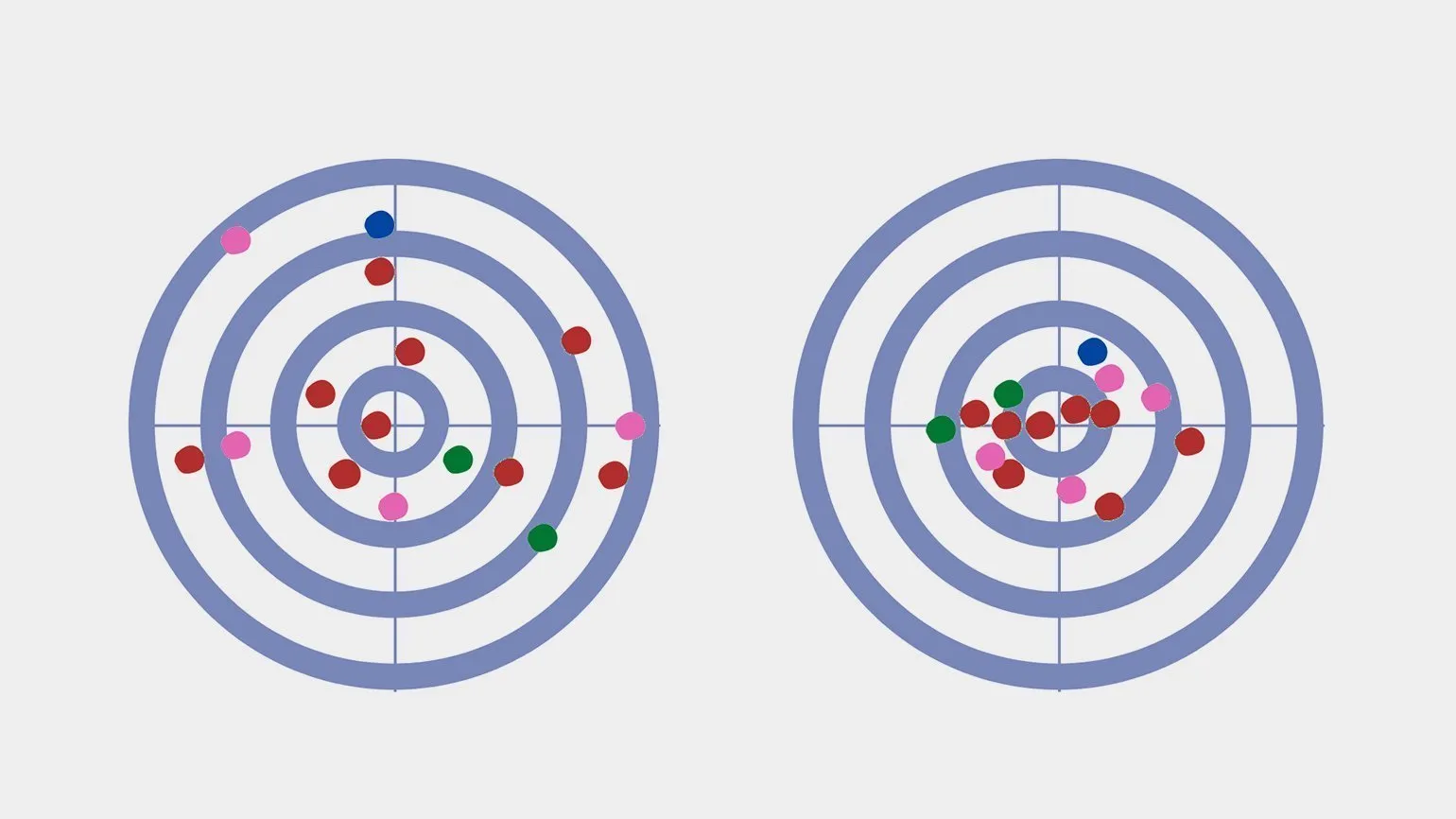
Изрешечённая мишень служит наглядным примером распределения результатов стрельбы. В этом контексте дисперсия можно рассматривать как обратную величину к кучности попаданий. Высокая кучность, означающая множество попаданий в одну и ту же точку, соответствует низкой дисперсии. Напротив, низкая кучность, характеризующая рассеяние попаданий, указывает на высокую дисперсию. Понимание этой взаимосвязи важно для анализа результатов стрельбы и улучшения навыков.

Понимание дисперсии: как она влияет на анализ данных

Дисперсия является важным показателем, который помогает не только оценивать разброс данных, но и составляет основу для более сложных статистических методов, таких как анализ вариаций и построение доверительных интервалов. Применение дисперсии в аналитике данных предоставляет исследователям и бизнес-аналитикам возможность делать более точные выводы и предсказания. Понимание дисперсии способствует улучшению качества анализа и повышению эффективности принятия решений на основе данных.

6. Дилемма смещения и дисперсии в машинном обучении

В машинном обучении смещение и дисперсия являются основными факторами, влияющими на общую ошибку предсказания модели. Оптимальная ситуация предполагает минимизацию как смещения, так и дисперсии, но на практике возникает проблема: снижение одной из этих величин часто приводит к увеличению другой. Это противоречие требует внимательного подхода при разработке и настройке моделей, чтобы достичь наилучших результатов в предсказаниях. Понимание взаимосвязи между смещением и дисперсией может помочь специалистам в области машинного обучения оптимизировать свои модели и улучшить их производительность.

Обучение модели представляет собой процесс разработки функции, график которой точно отражает данные из обучающего набора. Это дает возможность модели эффективно прогнозировать результаты на основе известных данных. Правильная интерпретация и адаптация функции к тренировочным данным являются ключевыми аспектами, обеспечивающими высокую точность предсказаний.

Если функция слишком сложна и перегружена деталями, это может негативно сказаться на ее способности к предсказанию на новых данных, что в итоге приводит к возникновению смещения. Понимание этой проблемы важно для разработки эффективных моделей, так как упрощение функции может повысить ее обобщающую способность и улучшить качество предсказаний.

Использование различных тренировочных наборов или датасетов может вызывать значительные колебания в предсказаниях, что указывает на высокий уровень дисперсии. Это подчеркивает важность выбора качественных и репрезентативных данных для обучения моделей, чтобы минимизировать неопределенность и повысить точность прогнозов. Правильный подход к формированию тренировочных наборов способствует более стабильным и надежным результатам в машинном обучении.

Сложные модели обычно характеризуются низким смещением, однако они более уязвимы к шуму и изменчивости новых данных, что может привести к нестабильности их предсказаний. К примеру, если снайпер настраивает прицел, принимая во внимание несущественные факторы, такие как цвет мишени, это негативно скажется на его точности в различных условиях. Это подчеркивает важность учета релевантных переменных при построении предсказательных моделей, чтобы обеспечить их надежность и точность в изменяющихся ситуациях.

Простые модели могут упускать ключевые параметры, что, несмотря на их способность делать точные предсказания, приводит к частым ошибкам. Это похоже на снайпера, который не учитывает ветер или расстояние до цели и, в результате, не попадает в мишень. Важно понимать, что для достижения высокой точности и надежности прогнозирования необходимо учитывать все значимые факторы.

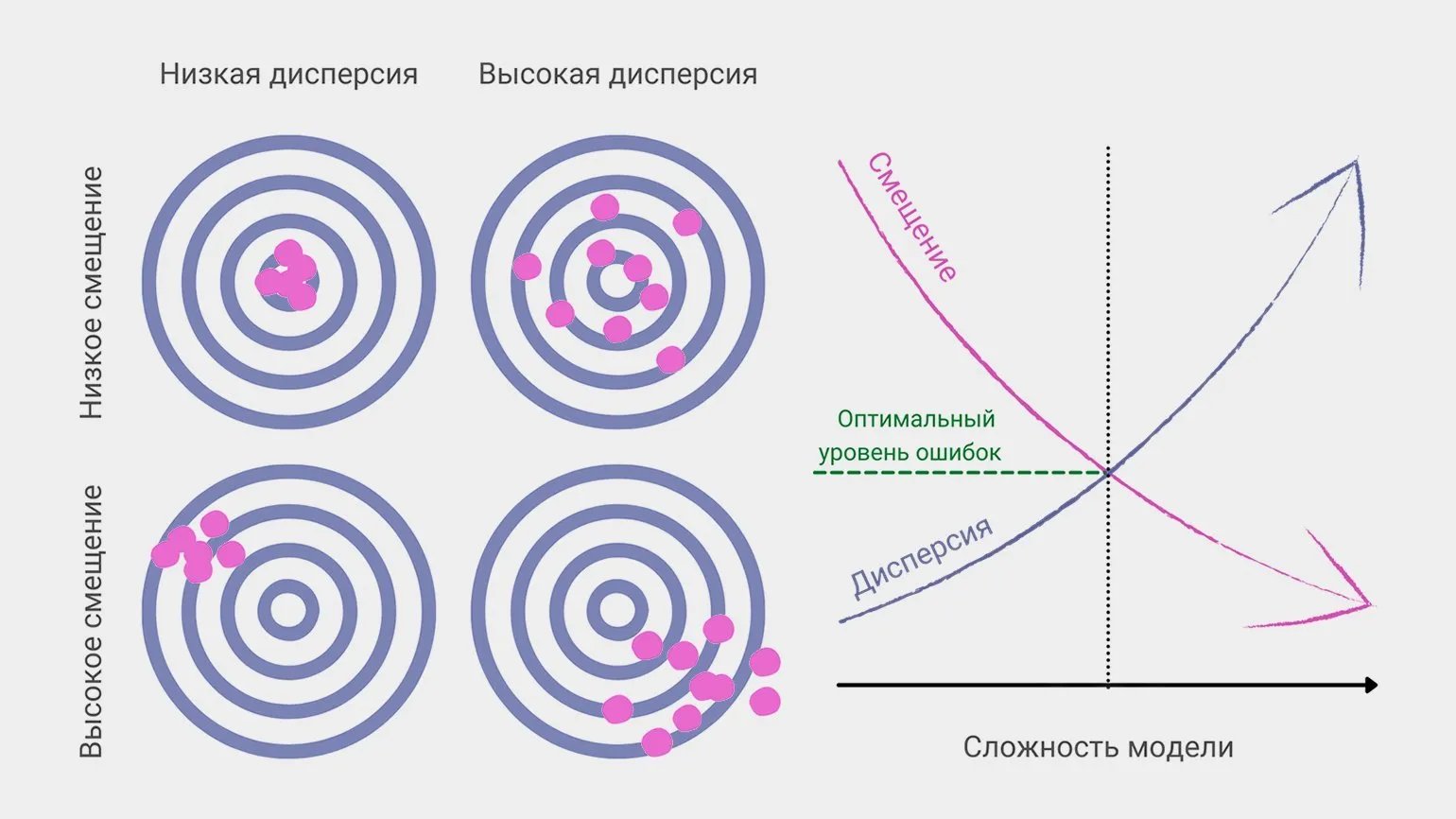
Дата-сайентист постоянно работает над достижением оптимального баланса между смещением и дисперсией с целью минимизации общей ошибки предсказания. Для этого необходимо провести тщательную настройку моделей и глубокое понимание характеристик данных. Эффективное управление смещением и дисперсией позволяет улучшить качество предсказаний и повысить точность аналитических выводов.

Эта дилемма выходит за рамки статистики и машинного обучения. В 2009 году проведенное исследование показало, что люди часто полагаются на эвристику «высокое смещение + низкая дисперсия»: мы можем допускать ошибки, но делаем это с высокой степенью уверенности. Это явление иллюстрирует, как уверенность в своих выводах может быть обманчивой и не всегда соотносится с реальной точностью. Понимание таких психологических механизмов важно для улучшения анализа данных и принятия решений, особенно в области, где доверие к результатам имеет критическое значение.

Эти наблюдения могут оказаться полезными для разработчиков, стремящихся создать искусственный интеллект, способный принимать более человечные решения и действовать с учетом эмоциональных и социальных факторов. Понимание этих аспектов поможет улучшить взаимодействие пользователей с ИИ и повысить его эффективность в различных сферах.

7. Корреляция: Понимание и Применение

Корреляция представляет собой статистическое явление, при котором наблюдается взаимосвязь между изменениями одной величины и изменениями другой. Однако стоит подчеркнуть, что наличие корреляции не означает, что одна величина вызывает изменения в другой. Этот принцип является ключевым при анализе данных и интерпретации результатов. Понимание корреляции и ее отличия от причинно-следственной связи важно для корректной оценки взаимосвязей и принятия обоснованных решений на основе статистики.

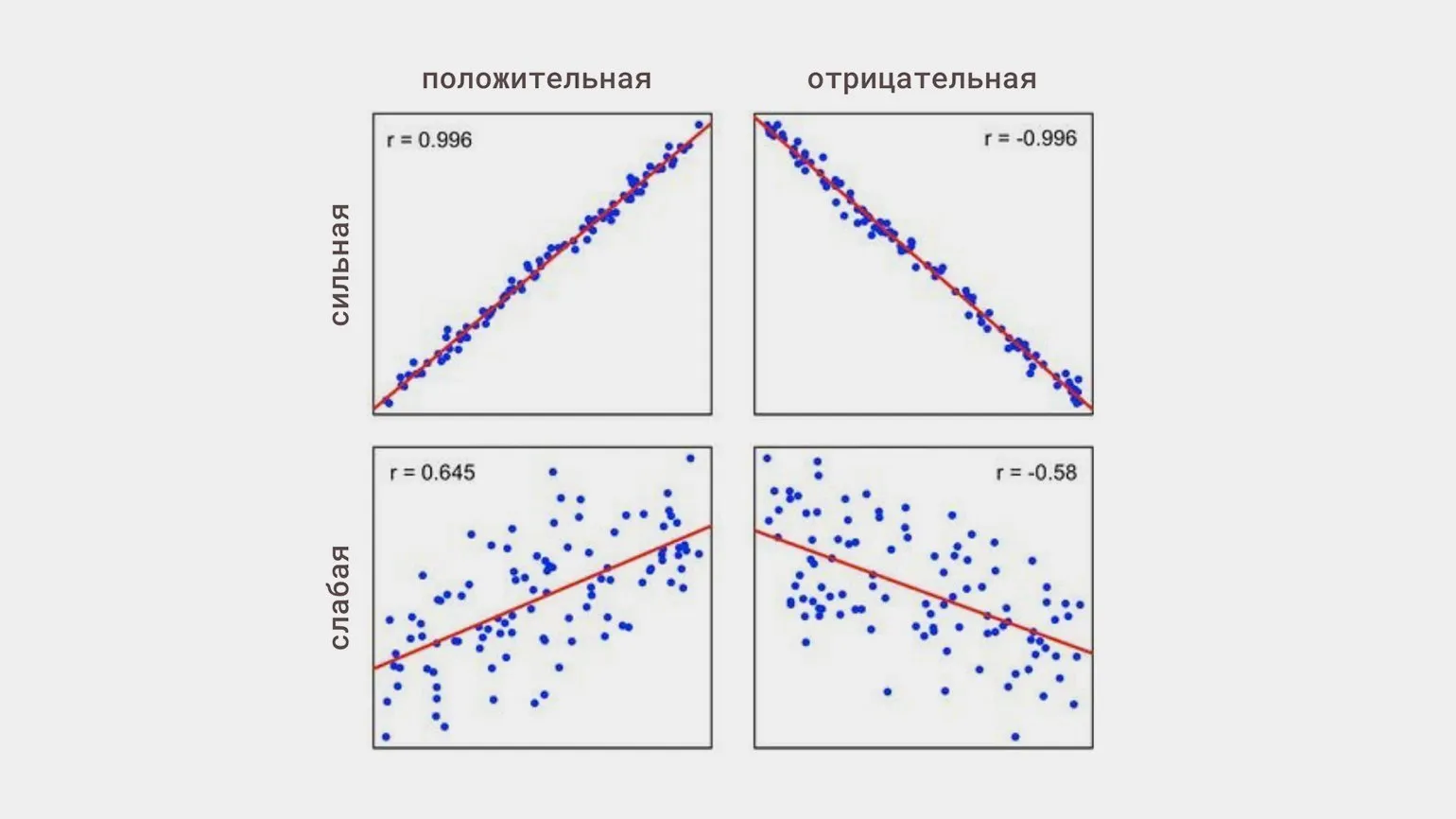
Линейная корреляция представляет собой связь между двумя переменными, при которой изменения одной переменной пропорционально влияют на изменения другой. Линейная корреляция может быть положительной, когда увеличение одной переменной сопровождается увеличением другой, или отрицательной, когда увеличение одной переменной приводит к уменьшению другой. Понимание линейной корреляции важно для анализа данных, так как она позволяет выявлять и quantifying связи между переменными. Применение линейной корреляции находит место в различных областях, таких как статистика, экономика и наука, что делает её важным инструментом для исследователей и аналитиков.

• положительной — обе величины увеличиваются или уменьшаются синхронно;
• отрицательной — при увеличении одной переменной другая уменьшается;
• сильной или слабой — независимо от направления взаимосвязи.

Корреляционный анализ представляет собой метод, который используется для изучения статистической зависимости между переменными. Его основная цель заключается в оценке степени связи между переменными, что помогает определить, какие из них следует включить в модель, а какие нет. Этот анализ позволяет выявить как положительные, так и отрицательные корреляции, что играет важную роль в построении эффективных статистических моделей и прогнозировании. Корреляционный анализ является ключевым инструментом в различных областях, включая экономику, социологию и медицину, поскольку он помогает исследователям и аналитикам лучше понимать взаимосвязи между различными факторами.

Важно отметить, что корреляция не всегда свидетельствует о наличии причинно-следственной связи. Даже если два показателя демонстрируют высокую корреляцию, это не означает, что они обязательно взаимосвязаны. Необходимо проводить более глубокий анализ, чтобы установить истинные причины изменений в данных и избежать ложных выводов.

Проект Spurious Correlations («Ложные корреляции») представляет собой уникальную платформу, на которой визуализируются графики, демонстрирующие корреляции между абсолютно несвязанными статистическими данными. Например, он иллюстрирует связь между числом утонувших в домашних бассейнах и количеством фильмов с Николасом Кейджем. Такие примеры подчеркивают важность критического мышления в анализе данных и предостерегают от необоснованных выводов на основе статистики. Способность различать истинные корреляции и случайные совпадения имеет значительное значение в исследованиях и принятии решений. Проект способствует повышению осведомленности о статистических уловках и помогает аудитории лучше понимать, как интерпретировать данные в современном мире.

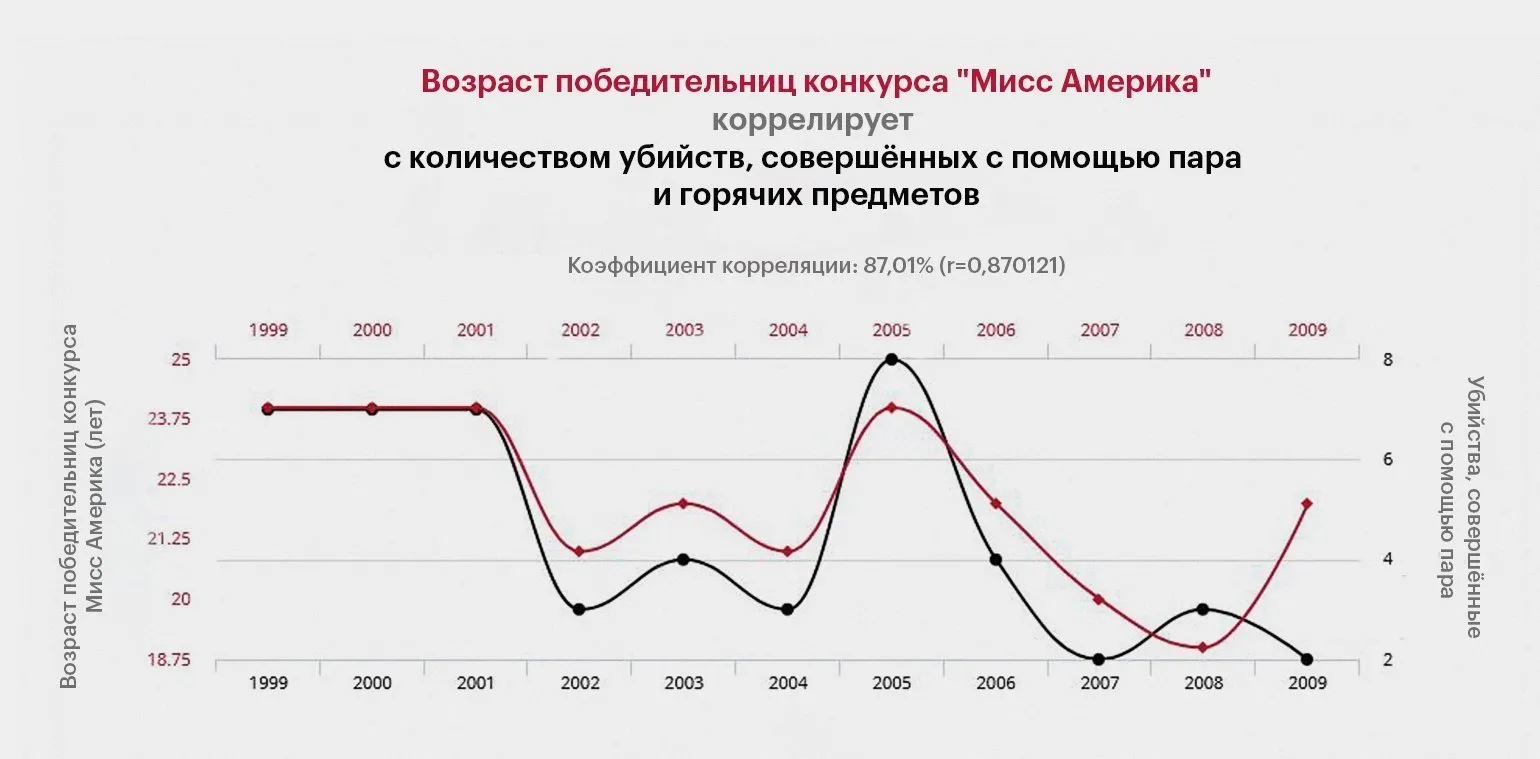
Постоянный анализ данных способствует предотвращению синдрома поиска глубинной связи (СПГС) и углубляет понимание статистических взаимосвязей. Регулярное обращение к статистической информации позволяет выявлять реальные тенденции и избегать ложных выводов, что особенно важно для исследователей и аналитиков. Это помогает принимать более обоснованные решения на основе фактических данных, а не измышлений.